Построение (конструирование) критерия оптимальности (функционала).
По условию задачи необходимо минимизировать энергию, затраченную на преодоление момента сопротивления и на нагрев.
Запишем эту энергию как интеграл от мгновенного значения мощности.
Мощность механических потерь составляет величину:
.
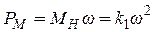Мощность энергетических потерь вычисляется по формуле:
.
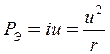Тогда мгновенное значение суммарной мощности примет вид:
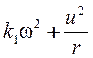. (15)
Поэтому функционал оптимальности (величина, подлежащая минимизации), представляющий собой суммарную энергию потерь, запишется в виде:
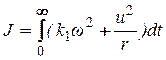. (16)
После введения обозначений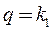 
, 
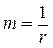критерий оптимальности запишется следующим образом:
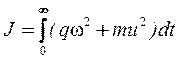. (17)
Решение задачи.
Соотношения (14) и (15) составляют условие задачи оптимального стабилизирующего управления, когда управление ищется в виде обратной связи: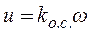 
, (18)
где 
– коэффициент обратной связи.
Решение задачи предлагается провести четырьмя методами.
Синтез регуляторов на основе метода вариационного исчисления
Метод основан на решении вариационной задачи на условный экстремум (задачи Лагранжа). Ниже приводится постановка задачи и алгоритм ее решения.
Постановка задачи.
Объект управления описывается векторно-матричным дифференциальным уравнением:
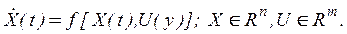(19)
Начальное положение объекта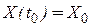 
. (20)
Конечное положение объекта 
. (21)
Критерий оптимальности, который является числовым показателем качества системы, задается в виде функционала:
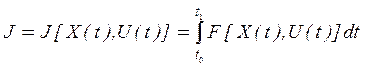. (22)
Определить управление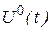 
, называемое оптимальным, переводящее объект управления из начального положения в конечное, и оптимальную траекторию 
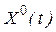, соответствующую этому управлению, на которых функционал принимает экстремальное значение.
|
|
|
Алгоритм решения задачи.
1. Составляется функция Лагранжа:
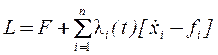, (23)
где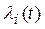 
– неопределенные множители Лагранжа.
2. Записываются уравнения Эйлера-Лагранжа:
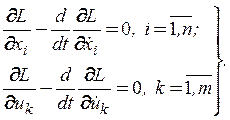(24)
3. Из системы уравнений Эйлера-Лагранжа и уравнений объекта находятся:
, 
.
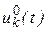Синтез регуляторов на основе метода динамического программирования
Синтез регуляторов на основе метода динамического программирования основан на функциональном уравнении метода динамического программирования, являющимся следствием принципа оптимальности Р. Беллмана.
Пусть задан объект управления, описываемый уравнениями:
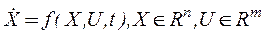. (25)
Требуется найти закон управления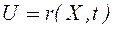 
, (26)
чтобы на движениях системы (25), (26), возбуждаемых произвольными начальными отклонениями, минимизировался функционал
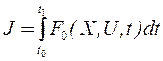. (27)
Функциональное уравнение метода динамического программирования Р. Беллмана имеет вид:
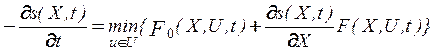, (28)
где через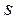 
обозначено значение функционала на оптимальных траекториях.
Напомним, что по определению производная от скалярной функции по векторному аргументу есть вектор-строка:
|
|
|
.
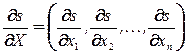Уравнение Беллмана (28) представляет собой дифференциальное уравнение в частных производных относительно скалярной функции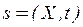 
, которая называется функцией Беллмана. Но это уравнение не является линейным из-за наличия в выражении (28) справа операции взятия минимума.
Замечание 1. Если ограничения на управления отсутствуют или минимум в правой части достигается во внутренней точке множества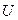 
, то уравнение Беллмана можно представить в виде:
; (29)
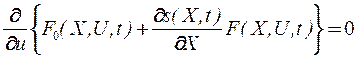. (30)
Уравнение (30) выражает необходимое условие минимума правой части (28) и заменяет опущенную в (29) операцию минимизации по управлению.
При этом уравнения (29) и (30) нужно решать при краевых условиях:
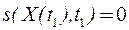. (31)
Замечание 2. В общем случае решение уравнения Беллмана – очень сложная задача. Однако для линейно-квадратичной задачи оптимизации (линейный объект, квадратичный функционал) уравнение Беллмана допускает аналитическое решение.
Алгоритм нахождения оптимального управления методом динамического программирования.
1. Из уравнения (30) определяется управление как функция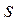 
, то есть 
.
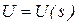2. 
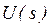подставляется в уравнение (29), которое решается затем при краевом условии 
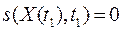, и находится функция Беллмана.
|
|
|
3. Найденная в пункте 2 функция Беллмана подставляется в выражение 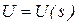и находится оптимальное управление как функция переменной Х, то есть 
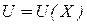. Таким образом, получается управление в виде обратной связи.
Синтез регуляторов на основе
метода аналитического конструирования регуляторов
Рассмотрим объект управления, возмущённое движение которого описывается в первом приближении уравнением
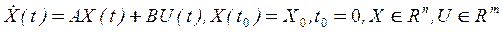, (32)
где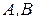 
– заданные матрицы чисел размерами n×n и n×m соответственно.
Требуется найти матрицу чисел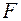 
уравнения регулятора:
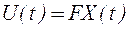, (33)
такую, чтобы на устойчивых движениях системы (32), (33), возмущенных произвольными начальными отклонениями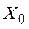 
, минимизировался функционал
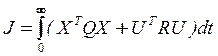, (34)
где Q и R – заданные положительно-определённые симметрические матрицы чисел размеров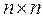 
и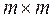 
(
, 
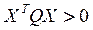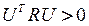для всех 
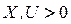, что обозначается 
).
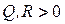Замечание. Для случая диагональной Q это означает положительность всех её элементов.
Матрица F называется матрицей коэффициентов усиления регулятора.
Используя метод динамического программирования, можно получить следующую процедуру аналитического конструирования регуляторов (АКОР).
1. Решение системы нелинейных алгебраических уравнений Риккати относительно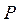 
:
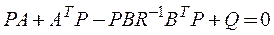, (35)
где 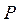– симметричная матрица размерности .
|
|
|
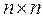2. Уравнение Риккати имеет множество решений (так как оно нелинейно). Из всего множества этих решений нужно выделить матрицу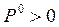 
.
3. Вычисление искомой матрицы коэффициентов усиления регулятора по формуле: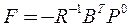 
. (36)
Можно показать, что полученная таким образом матрица F обеспечивает асимптотическую устойчивость системы (32), (33), то есть
.
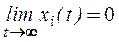Синтез регуляторов на основе
принципа максимума Л.С. Понтрягина
Рассмотрим этот принцип на примере управления объектом
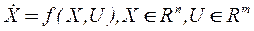, (37)
для которого заданы
1) краевые условия:
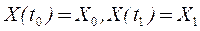, (38)
2) функционал:
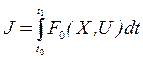, (39)
3) ограничения на управления: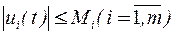 
, (40)
где Мi – заданные положительные числа.
Задача. Перевести объект управления из заданного начального состояния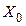 
в заданное конечное состояние 
за время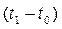 
так, чтобы функционал (39) принимал максимальное значение.
Для решения этой задачи используем метод Лагранжа.
Введем в рассмотрение
1) расширенный вектор состояний:
,
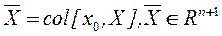для которого координата x0(t) характеризует текущее значение функционала (39):
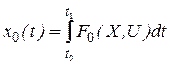, (41)
откуда следует:
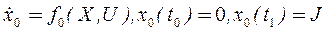; (42)
2) вектор множителей Лагранжа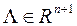 
, используемый для конструирования функции многих переменных, называемой гамильтонианом:
.
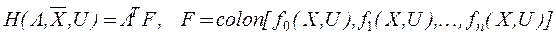Необходимое условие экстремума гамильтониана (как функции многих переменных), как известно из математического анализа, состоит в равенстве нулю полной производной по времени от него:
. (43)
Для того, чтобы выполнить (43), будем полагать, что справедливы следующие равенства:
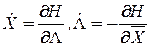, (44)
подстановка которых в (43) даёт:
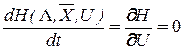. (45)
Тем самым, цель управления, формируемого в соответствии с принципом максимума, состоит в выполнении
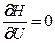(46)
или в выполнении необходимого условия экстремума составляющей гамильтониана, зависящей от управлений.
Поскольку константа определяется с точностью до множителя, в дальнейшем, без потери общности, будем полагать 
.
ЛИТЕРАТУРА
ОСНОВНАЯ
1. Абдуллаев Н.Д. Теория и методы проектирования оптимальных регуляторов / Н.Д. Абдуллаев, Ю.П. Петров. Л.: Энергоатомиздат, 1985.
2. Александров А.Г. Оптимальные и адаптивные системы /
А.Г. Александров. – М.: Высшая школа, 1989.
3. Ванько В.И. Вариационное исчисление и оптимальное управление: учебник для вузов / В.И. Ванько, О.В. Ермошина,
Г.Н. Кувыркин; под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.
4. Воронов А.А. Основы автоматического регулирования и управления / А.А. Воронов, В.К. Титов, Б.Н. Новограмов. – М.: Высшая школа, 1977.
5. Гноенский Л.С. Математические основы теории управляемых систем / Л.С. Гноенский, Г.А. Каменский, Л.Э. Эльсгольц. – М.: Наука, 1969.
6. Дерусоо Г. Пространство состояний в теории управления /
Г. Дерусоо, Р. Рой, Ч. Клоуз. – М.: Наука, 1970.
7. Директор Р. Введение в теорию систем / Р. Директор, С. Рорер. – М.: Высшая школа, 1971.
8. Олейников В.А. Основы оптимального и экстремального управления / В.А. Олейников, Н.С. Зотов, А.М. Пришвин. – М.: 1969.
9. Сигорский В.П. Математический аппарат инженера /
В.П. Сигорский. – Киев: Техника, 1977.
10. Теория автоматического управления: в 2 ч. / под ред.
А.А. Воронова. – М.: Высшая школа, 1986.
11. Тимофеев Ю.К. Вариационное исчисление в оптимальном управлении: учеб. пособие / Ю.К. Тимофеев. – Саратов: СГТУ, 2003.
12. Тимофеев Ю.К. Основы описания линейных динамических систем: учеб. пособие / Ю.К. Тимофеев, О.Ю. Торгашова. – Саратов: СГТУ, 2004.
13. Ту Ю. Современная теория управления / Ю. Ту. – М.: Машиностроение, 1971.
14. Эльсгольц Л.Э. Дифференциальные уравнения в вариационном исчислении / Л.Э. Эльсгольц. – М.: Наука, 1965.
ДОПОЛНИТЕЛЬНАЯ
1. Алексеев В.М. Сборник задач по оптимизации / В.М. Алексеев, Э.М. Галеев, В.М. Тихомиров. – М.: Наука, 1984.
2. Бессонов А.А. Линейные электрические цепи / А.А. Бессонов. – М.: Высшая школа, 1983.
3. Дорф Р. Современные системы управления / Р. Дорф, Р. Бишоп. – М.: Лаборатория базовых знаний, 2002.
4. Куропаткин П.В. Оптимальные и адаптивные системы /
П.В. Куропаткин. – М.: Высшая школа, 1980.
5. Проектирование следящих систем с помощью ЭВМ / под ред.
В.С. Медведева. – М.: Машиностроение, 1979.
6. Сборник задач по теории автоматического управления / под ред. В.А. Бесекерского. – М.: Наука, 1973.
7. Теория автоматического управления: в 2 ч. / под ред.
А.В. Нетушила. – М.: Высшая школа, 1976, 1983.
ОСНОВЫ ТЕОРИИ
ОПТИМАЛЬНОГОУПРАВЛЕНИЯ
Дата добавления: 2016-01-04; просмотров: 51; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!