Сформулировать теорему о базисном миноре.
Теорема. Столбцы матрицы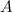 
, входящие в базисный минор, образуют линейно независимую систему. Любой столбец матрицы 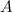линейно выражается через остальные столбцы из базисного минора. В матрице 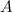размеров 
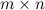минор 
-го порядка называется базисным, если он отличен от нуля, а все миноры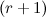 
-ro порядка равны нулю или их вообще не существует.
Следствие. Если все столбцы матрицы 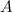линейно выражаются через столбцов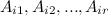 
, которые образуют линейно независимую систему, то ранг матрицы 
.
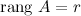Сформулировать теорему об инвариантности ранга при элементарных преобразованиях матрицы.
Ранг матрицы не меняется при элементарных преобразованиях ее строк и столбцов.
Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение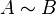 
для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если 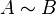, то их ранги равны.
Перечислить различные формы записи системы линейных алгебраических уравнений (СЛАУ). Какая СЛАУ называется совместной?
Формы записи:
-координатная
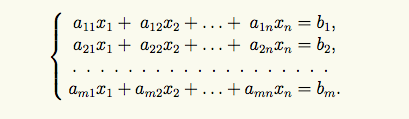
-векторная
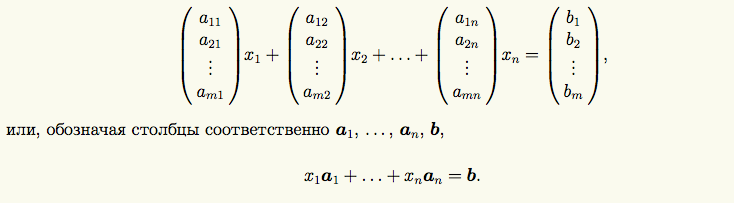
-матричная
СЛАУ называют совместной, если она имеет какие либо решения. В противном случае ее называют несовместной.
Дата добавления: 2016-01-03; просмотров: 24; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!