Циклы в вычислительных алгоритмах

Определение 4. Циклические алгоритмы – алгоритмы, содержащие фрагменты повторения вычислений.

В зависимости от того, известно ли наперед число повторений некоторого участка алгоритма или нет, выделяют циклы арифметические и итерационные.

В арифметических циклах число повторений вычислений известно и определяется счетчиком цикла. При каждом очередном вычислении значение счетчика изменяется на заданную величину и сравнивается с установленным количеством повторений. Если эти величины совпадают, то происходит выход из цикла по счетчику. В противном случае повторения вычислений продолжаются. Если перед началом цикла значение счетчика превышает заданное число повторений, то цикл не выполняется вообще. Возможен принудительный выход из цикла по некоторому наперед заданному значению.

В итерационных циклах число повторений неизвестно, выход из цикла осуществляется при выполнении некоторого условия. В случае, когда условие проверяется до начала повторений, циклы называются с предусловием, когда же проверка происходит после очередной итерации, циклы называются с постусловием. Все арифметические циклы – это циклы с предусловием. [2]

Общий вид блок-схем циклических алгоритмов представлен в таблице 2.

Рассмотрим примеры решения задач с помощью циклических алгоритмов. В Приложении 1 представлены программы на языке Pascal, соответствующие данным задачам.

Задача 4.

1. Составить алгоритм вычисления функции .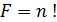

2. 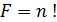. – произведение 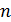натуральных чисел 1*2*3…n, 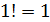. Вычисление значения факториала можно рассматривать как последовательное повторение операции умножения предшествующего значения факториала F на очередное натуральное число.

3. 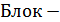схема алгоритма вычисления факториала 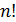на рис.5.

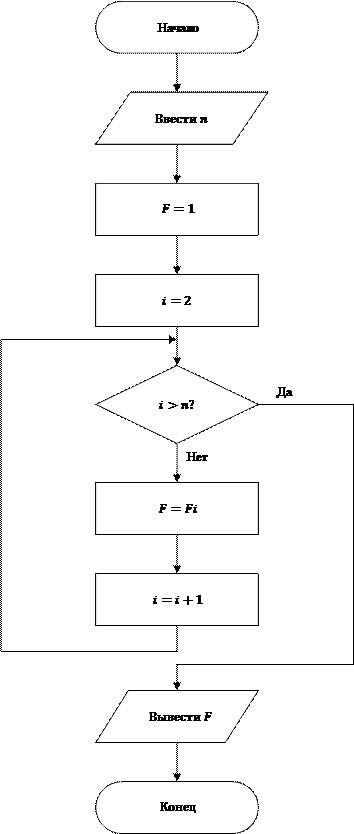Рис. 5 Алгоритм вычисления функции n!

Задача 5.

1. Составить алгоритм вычисления выражения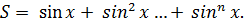

2. Если взять начальное значение суммы 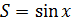, то повторяющимся действием будет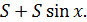

3. схема алгоритма представлена на рис.6.

Задача 6.

1. Составить алгоритм нахождения наибольшего общего делителя двух целых чисел a и b. [6]

2. Наибольший общий делитель (НОД) двух целых чисел a и b – это наибольшее целое число, которое делит нацело оба числа. Рассмотрим способ, который называется алгоритмом Евклида. Пусть a и b одновременно не равные нулю целые неотрицательные числа и a 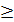b. Если b = 0, то НОД(a, b) = a, а если b 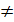0, то для чисел a,b и r, где r – остаток от деления a на b, выполняется равенство НОД (a, b) = НОД(b, r). Действительно, r:= a Mod b, r:= a –(a Div b) * b. Если какое-то число делит нацело и a, и b, то из приведенного равенства следует, что оно делит нацело и число r.

3. Блок-схема алгоритма Евклида нахождения НОД и НОК двух целых чисел на рис.7.

4. Программная реализация алгоритма Евклида (Приложение 1, Evclid.pas).

Задача 7.

1. Дано натуральное число n. Требуется подсчитать количество цифр данного числа.

2. Количество цифр в числе n неизвестно, поэтому необходимо использовать цикл с предусловием. Подсчёт количества цифр можно начать с последней цифры числа, далее увеличить изначально нулевой счётчик цифр на единицу. Повторять уменьшение числа в 10 раз, пока оно не станет равным 0.

3. Блок-схема на рис.8.

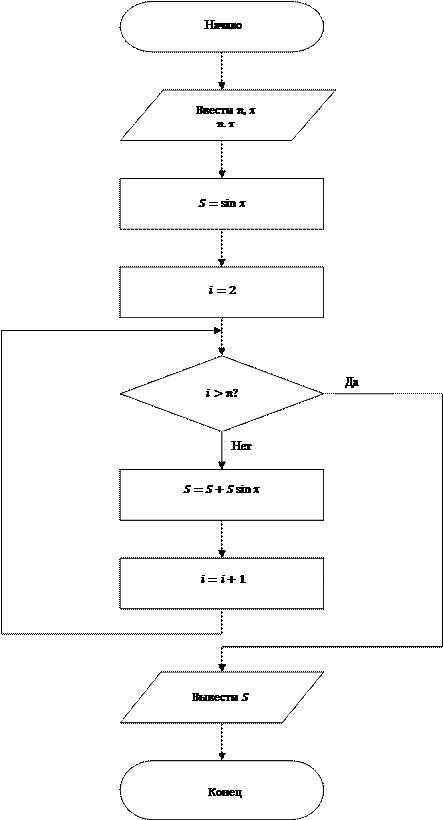
Рис. 6 Алгоритм вычисления выражения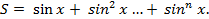

Рис.7 Алгоритм Евклида нахождения НОД и НОК двух целых чисел

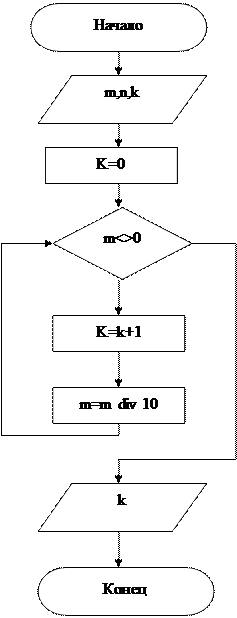
Рис.8 Алгоритм подсчета количества цифр в натуральном числе.

4. Программа для решения задачи 7 (подсчет количества цифр в числе) представлена в Приложении 1, Program7.pas.

МАШИНА ПОСТА

В 1936 году американский математик и логик Эмиль Леон Пост (1897–1954) предложил абстрактную вычислительную конструкцию, позволяющую формально определить алгоритм и названную впоследствии машиной Поста. При разработке вычислительной конструкции Пост руководствовался принципом создания максимально простой абстракции: минимумом операций при обработке информации, входная информация должна быть закодирована с использованием минимального набора символов.

В теории алгоритмов существует так называемый “тезис Поста”: “Всякий алгоритм представим в форме машины Поста”. Этот тезис одновременно является формальным определением алгоритма. Алгоритм(по Посту) — программа для машины Поста, приводящая к решению поставленной задачи.

Тезис Поста является гипотезой. Его невозможно строго доказать (так же, как и тезис Тьюринга), потому что в нем фигурируют, с одной стороны, интуитивное понятие “всякий алгоритм”, а с другой стороны — точное понятие “машина Поста”. Для того чтобы опровергнуть гипотезу Поста, необходимо придумать алгоритм, который невозможно записать в виде программы для машины Поста. На сегодняшний день такого алгоритма не существует. [12]

Состав машины Поста.

Машина Поста состоит из ленты и каретки. Лента бесконечна и разделена на секции одинакового размера — ячейки.

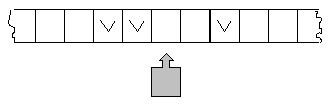
Рис. 9. Состав машины Поста

В каждой ячейке ленты может стоять метка V либо ничего не записано.. Состояние ленты — это распределение меток по ячейкам. Состояние ленты меняется в процессе работы машины.

Каретка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, она стоит против ровно одной ячейки ленты, т.е. каретка обозревает одну ячейку. За единицу времени каретка может совершить одно из трех действий: стереть метку, поставить метку, совершить движение на соседнюю ячейку. Состояние машины Поста складывается из состояния ленты и положения каретки.

Команды машины Поста:

1. записать 1 (метку), перейти к i -й строке программы;

2. записать 0 (стереть метку), перейти к i -й строке программы;

3. сдвиг влево, перейти к i -й строке программы;

4. сдвиг вправо, перейти к i -й строке программы;

5. останов;

6. если 0, то перейти к i, иначе перейти к j.

Недопустимые действия, ведущих к аварийной остановке машины:

· попытка записать 1 (метку) в заполненную ячейку;

· попытка стереть метку в пустой ячейке;

· бесконечное выполнение (зацикливание).

Команды машины обозначают следующим образом (рис.10):

Рис. 10 Команды машины Поста

Рассмотрим несколько арифметических задач для машины Поста и их решение.[12]

С помощью простейших операций, которыми располагает машина Поста, можно выполнять арифметические операции — основу любого современного процессора.

1. На ленте задан массив меток. Увеличить длину массива на 2 метки. Каретка находится либо слева от массива, либо над одной из ячеек самого массива. (увеличение числа на 2).

Решение:

1.? 2; 3 (команды 1 и 2 — передвигаем каретку к массиву)

2. → 1

3. → 4 (команды 3 и 4 — передвигаем каретку к концу массива)

4.? 5; 3

5. V 6 (команды 5–7 — ставим 2 метки в конце массива)

6. → 7

7. V 8

8.!

2. Даны два массива меток, которые находятся на некотором расстоянии друг от друга. Требуется соединить их в один массив. Каретка находится над крайней левой меткой первого массива. (сложение двух чисел)

Решение.

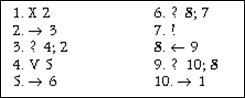
3. На ленте задана последовательность массивов, включающая в себя один и более массивов. При этом два соседних массива отделены друг от друга одной пустой ячейкой. Необходимо на ленте оставить один массив длиной равной сумме длин массивов, присутствовавших изначально. Каретка находится над крайней левой меткой первого (левого) массива.

Решение.

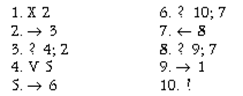
4. На ленте заданы два массива — m и n, m > n. Вычислить разность этих массивов. Каретка располагается над левой ячейкой правого массива.

Решение:

1. → 2 (команды 1–3: ищем левую метку массива m)

2.? 3; 1

3. ← 4

4. X 5 (стираем левую метку массива m)

5.? 6; 7

6. → 5

7. X 8 (стираем левую метку массива n)

8. → 9

9.? 12; 10 (стерли последнюю метку в массиве n?)

10. ←11 (ищем левый край массива m)

11.? 10; 4

12.!

5. На ленте задан массив. Удвоить массив в два раза. Каретка располагается над первой ячейкой массива.

Решение.

В результате работы программы справа от исходного массива будет сформирован новый массив удвоенной длины, исходный массив будет стерт.

МАШИНА ТЬЮРИНГА

Абстрактная вычислительная машина, предложенная в 1936 году А. Тьюрингом для уточнения понятия алгоритма. Доказано, что машина Тьюринга по своим возможностям эквивалентна машине Поста.

Состав Машины Тьюринга.

Машина Тьюринга состоит из каретки и бесконечной ленты, разбитой на ячейки. Каждая ячейка ленты может содержать символ из некоторого алфавита A={a₀,a₁,…,a_N}. Любой алфавит содержит символ «пробел», который обозначается как a₀ или Λ. При вводе команд пробел заменяется знаком подчеркивания « _ ».

Машина Тьюринга — это автомат, управляемый таблицей. Строки в таблице соответствуют символам выбранного алфавита A , а столбцы — состояниям автомата Q={q₀,q₁,…,q_M } . В начале работы машина Тьюринга находится в состоянии q₁. Состояние q₀ — это конечное состояние: попав в него, автомат заканчивает работу.[11]

В каждой клетке таблицы, соответствующей некоторому символу a_i и некоторому состоянию q _j , находится команда, состоящая из трех частей:

1. символ из алфавита A ;

2. направление перемещения: > (вправо), < (влево) или . (на месте);

3. новое состояние автомата.

Примеры решения задач с помощью машины Тьюринга рассмотрим далее.

1. Составить алгоритм, прибавляющий единицу к последней цифре заданного числа, расположенного на ленте. Входные данные – слово – цифры целого десятичного числа, записанные в последовательные ячейки на ленту. В первоначальный момент устройство располагается напротив самого правого символа – цифры числа.

Решение. В случае если последняя цифра равняется 9, то ее нужно заменить на 0 и затем прибавить единицу к предшествующему символу. Программа в этом случае для данного устройства Тьюринга может быть написана так:

	a₀					…
q₁	1 H q₀	1 H q₀	2 H q₀	3 H q₀	4 H q₀		8 H q₀	9 H q₀	0 λ q₀

Здесь q₁ — состояние изменения цифры, q₀ — остановка. Если в q₁ автомат фиксирует элемент из ряда 0..8, то он замещает ее на один из 1..9 соответственно и затем переключается в состояние q₀, то есть устройство останавливается. В случае если же каретка фиксирует число 9, то замещает ее на 0, затем перемещается влево, останавливаясь в состоянии q₁. Такое движение продолжается до того момента, пока устройство не зафиксирует цифру, меньшую 9. Если все символы оказались равными 9, они замещаются нулями, на месте старшего элемента запишется 0, каретка переместится влево и запишет 1 в пустую клетку. Следующим шагом будет переход в состояние q₀– остановка.

2. Дан ряд из символов, обозначающих открывающие и закрывающие скобки. Требуется создать программу для машины Тьюринга, которая выполняла бы удаление пары взаимных скобок, то есть элементов, расположенных подряд – “()”. Например, исходные данные: “) (() (()”, ответ должен быть таким: “)... ((”.

Решение. Механизм, находясь в q₁, анализирует крайний слева элемент в строке.

Состояние q₁: если встречен символ “(”, то совершить сдвиг вправо и переход в положение q₂; если определен “a₀”, то остановка.

Состояние q₂: проводится анализ скобки “(” на наличие парности, в случае совпадения должно получиться “)”. Если элемент парный, то сделать возврат каретки влево и перейти в q₃.

Состояние q₃: осуществить удаление сначала символа “(”, а затем “)” и перейти в q₁.

	a₀	(	)
q₁	a₀ H q₀	(П q₂	) П q₁
q₂	a₀ H q₀	(П q₂	) λ q₃
q₃	a₀ H q₀	a₀ П q₃	a₀ П q₁

Для проверки и отладки программ для машины Поста и машины Тьюринга можно использовать тренажёр «Машина Поста» и «Машина Тьюринга». В Интернет можно найти свободно распространяемые имитаторы как машины Поста, так и машины Тьюринга. [9]

Дата добавления: 2016-01-03; просмотров: 24; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!