Кривизны в сечениях гравитационного сопровождающего трёхгранника

Кривизны главных сечений

Кривизны главных сечений с учетом высоты после разложения в ряд Тейлора  (фактически используем примерные равенства 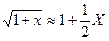 и ) будут иметь вид

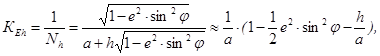
                                                                                                                                        (3.8)

Такое упрощение при вычислении кривизны на широте 45° и высоте 10000 м даёт ошибку в пересчёте на радиус, равную 40 м для 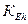 и  80 м для .

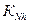Кривизны произвольных сечений

 

 

Кривизна нормального сечения в направлении, составляющем угол А с плоскостью меридиана (рис. 3.1), отыщется как:

                                                               

где dS – приращение длины дуги сечения;

       dα – угол поворота нормали к поверхности при перемещении вдоль участка дуги длиной dS .

Зададимся величиной dS и получим выражение для dα. Очевидно, что приращение длины дуги меридиана составит при этом величину dN = dS·cosA , а первого вертикала – величину d Е = dS·sinA . Углы dα_N и dα_Е поворота нормали к эллипсоиду при движении вдоль участков dN и d Е составят соответственно dα_N = dN / R_N , dα_Е = d Е / R _Е. Выразив величину dα в виде

dα = dα_N·cosA + dα_Е·sinA = dN / R_N ·cosA + d Е / R _Е ·sinA = dS·cos ² A / R_N + dS·sin ² A / R _Е ,

легко получить формулу для расчета кривизны K_A и радиуса кривизны R_A нормального сечения плоскостью, составляющей угол А с плоскостью меридиана, известную как формулу Эйлера:

                                                  (3.9

                         

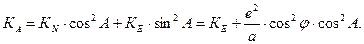
Представляет определенный интерес также среднее значение радиуса кривизны нормального сечения эллипсоида в точке, которое рассчитывается как [8]:

.                 

 

Сопровождающие трехгранники

Опираясь на понятие географической, геоцентрической и гравитационной вертикалей, введем трехгранники OENH, OE ¢ N ¢ H ¢, OE ² N ² H ². Вершины всех трехгранников совместим с текущей точкой. В трехграннике OENH ось OH направим вдоль географической вертикали вверх, ось ON - по касательной к меридиану на север, ось OE - по касательной к параллели на восток. Будем называть OENH – географическим сопровождающим трехгранником. Аналогично OE ¢ N ¢ H ¢ назовем геоцентрическим сопровождающим трехгранником, а OE ² N ² H ² - гравитационным сопровождающим трехгранником. Оси ON ¢, ON ²  поместим в плоскость меридиана проходящего через  ось ON, оси OH ¢, OH ² направим, соответственно, по геоцентрической и гравитационной вертикалям.

Кривизны в сечениях географического сопровождающего трехгранника

Для географического сопровождающего трёхгранника радиусами кривизны главных сечений являются 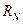 = M, 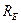 = N, см. (3.1) и 3.2). Радиусами кривизны точки, находящейся на высоте h, являются 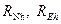, см. (3.5) и (3.7). Кривизнами точки на высоте  h  являются: 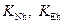, см. (3.8).

Кривизны в сечениях геоцентрического сопровождающего трёхгранника

Радиус-вектор r точки на поверхности эллипсоида определяется, исходя из следующих соображений.

Для меридионального сечения эллипсоида справедливо уравнение

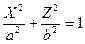следовательно       

Воспользуемся соотношением 1.0 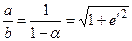, тогда основная формула приобретает вид

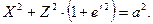
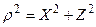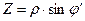Используем очевидные соотношения   и , получим

   отсюда

.                                                                   (3.10)

Как следует из Рисунка 1.6, радиус-вектор точки, находящейся на высоте h, увеличивается на величину 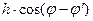. Из-за малости различий в широтах пренебрежём косинусом, тогда радиус-вектор точки, находящейся на высоте h, определяется формулой

.                                                                (3.11)

Очевидно, при представлении Земли в виде шара с радиусом r имеем равенство

.

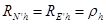После разложения в ряд имеем:

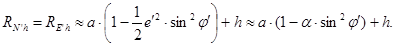
Кривизны имеют следующий вид:

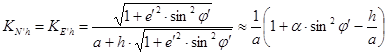.                   (3.12)

Кривизны в сечениях гравитационного сопровождающего трёхгранника

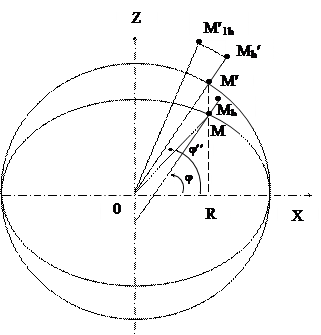
В соответствии с Разделом 2 не будем делать различий между гравитационной широтой и приведенной широтой, и все рассуждения будем делать для приведенной широты.

Из Рисунка 3.3 очевидно

X = OR + h× cosj = a × cosj² + h× cosj,

Z = RM + h × sin j.

Из (1.16) следует: 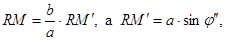 тогда

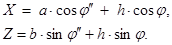                                                                          (3.13)

 

 

				dZ
		Рисунок 3. 3

M¢1h

 

 

Для пространственного трехгранника имеют место те же преобразования с тем отличием, что координаты Х и Y получаются из Х проектированием на плоскость нулевого меридиана и перпендикулярную ей.

Соответствующие формулы имеют вид

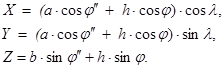                                                             (3.14)

Зададимся целью определить радиус кривизны в точке .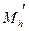

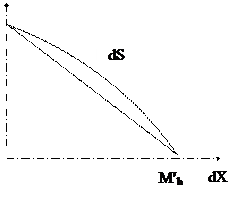
Пусть dS – бесконечно малая дуга 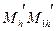, соответствующая приращению d j ².

Тогда

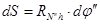.                                                                                           (3.15)

Проведя через точки 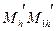 прямые, параллельные осям координат, получим треугольник. Из треугольника будем иметь

,

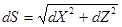приращения dX, dZ получим  на основе (3.13).

При этом учтем на основании (1.20)

                         (3.16)

Тогда

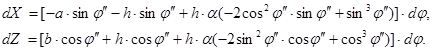
В результате подстановки в исходное уравнение и отбрасывания членов второго порядка малости получим:

.

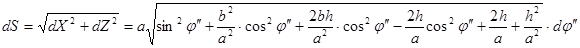Учитывая (3.15) и используя равенство , получим:

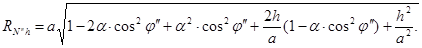
Не будет большой ошибки, если 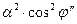 заменить на 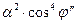, тогда

В результате

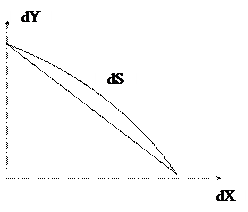
Аналогичные рассуждения применимы для определения кривизны в плоскости, перпендикулярной меридианной.

 

M¢2

 

 

Mh¢

 

Рисунок 4.4

 

 

Пусть dS – бесконечно малая дуга M_h ¢ M ¢₂, соответствующая приращению  d l.

Тогда 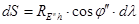.                                                              (3.17)

В свою очередь 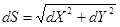. Из (4.14) имеем

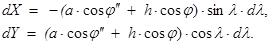
Следовательно        .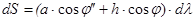

Учитывая (4.17) имеем .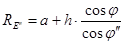

Учитывая незначительное различие в 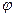 и 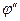, пренебрежём последним отношением.

Окончательно                                                              (3.18)

           .

Кривизны

 

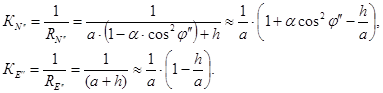              (3.19)

 

 

---

Дата добавления: 2022-12-03; просмотров: 24; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!