СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ В ТОЧКЕ
Определение 1. Функция  называется непрерывной в точке
называется непрерывной в точке 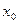 , если она задана в этой точке и в некоторой её окрестности и если
, если она задана в этой точке и в некоторой её окрестности и если  .
.
Пример:
Функция  непрерывна в любой точке
непрерывна в любой точке 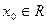 и поэтому
и поэтому  , например,
, например, 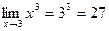 .
.
Согласно данному определению, непрерывность функции  в точке
в точке 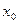 означает одновременную выполнимость следующих условий:
означает одновременную выполнимость следующих условий:
1) функция  должна быть задана в точке
должна быть задана в точке 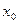 и в некоторой её окрестности;
и в некоторой её окрестности;
2) существуют  и
и 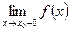 ;
;
3) 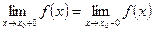 ;
;
4) 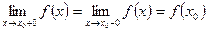 .
.
Если хотя бы одно из условий 1) - 4) не выполняется, то функция 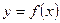 будет разрывной в точке
будет разрывной в точке 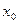 , а точка
, а точка 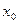 называется точкой разрыва функции
называется точкой разрыва функции 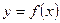 .
.
Классификация точек разрыва
1. точки устранимого разрыва;
2. точки разрыва первого рода (скачки);
3. точки разрыва второго рода.
Определение 2. Точка 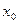 называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции  , если существует
, если существует  , но
, но  или значение функции
или значение функции  в точке
в точке 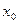 не задано.
не задано.
Определение 3. Точка 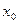 называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции  , если существуют конечные односторонние пределы
, если существуют конечные односторонние пределы  и
и 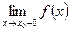 , но они различны, следовательно,
, но они различны, следовательно,  не существует.
не существует.
Определение 4. Точка 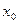 называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции  , если хотя бы один из односторонних пределов бесконечен или не существует.
, если хотя бы один из односторонних пределов бесконечен или не существует.
Свойства функций, непрерывных в точке.
Теорема 1. Сумма (разность) конечного числа функций, непрерывных в точке 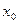 , есть функция, непрерывная в точке
, есть функция, непрерывная в точке 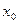 .
.
Теорема 2. Произведение конечного числа функций, непрерывных в точке 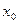 , есть функция, непрерывная в точке
, есть функция, непрерывная в точке 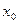 .
.
|
|
|
Теорема 3. Частное двух функций, непрерывных в точке 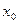 , есть функция, непрерывная в этой точке, если значение функции, стоящей в знаменателе, отлично от нуля в точке
, есть функция, непрерывная в этой точке, если значение функции, стоящей в знаменателе, отлично от нуля в точке 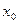 .
.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ НА МНОЖЕСТВЕ
Определение 1. Если функция непрерывна в каждой точке интервала  , то она непрерывна на этом интервале.
, то она непрерывна на этом интервале.
Определение 2. Функция  называется непрерывной на отрезке
называется непрерывной на отрезке  , если она непрерывна на интервале
, если она непрерывна на интервале  и
и 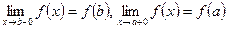 .
.
Теорема 1. Пусть функция 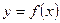 непрерывна на отрезке
непрерывна на отрезке  и на концах этого отрезка принимает значения разных знаков, тогда между точками a и b найдется, по крайней мере, одна точка
и на концах этого отрезка принимает значения разных знаков, тогда между точками a и b найдется, по крайней мере, одна точка  , в которой функция обращается в нуль:
, в которой функция обращается в нуль:
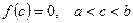 .
.
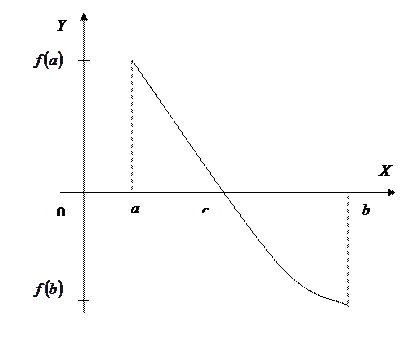
Геометрический смысл теоремы:
График непрерывной функции 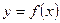 , соединяющий точки
, соединяющий точки 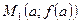 и
и 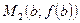 , где
, где 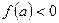 и
и  (или
(или 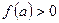 и
и  ), пересекает ось
), пересекает ось  по крайней мере в одной точке.
по крайней мере в одной точке.
Теорема 2. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то среди значений, принимаемых ею на этом отрезке, существуют наименьшее и наибольшее значения. При этом она принимает все значения между наибольшим и наименьшим значениями.
, то среди значений, принимаемых ею на этом отрезке, существуют наименьшее и наибольшее значения. При этом она принимает все значения между наибольшим и наименьшим значениями.
Дата добавления: 2022-07-02; просмотров: 21; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
