НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ.
Предел функции
Определение 1. Пусть функция 
определена в некоторой окрестности точки a, кроме, может быть, самой точки a. Число A называется пределом функции в точке a (или при x, стремящемся к a), если для любой последовательности допустимых значений аргумента 
, сходящейся к a (т.е. 
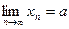), последовательность соответствующих значений функции 
сходится к числу A. В этом случае пишут 
или 
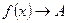при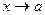 
.
Теорема. Функция не может иметь двух разных пределов в точке.
Бесконечно большие и бесконечно малые функции
Определение 2. Функция является бесконечно большой при 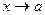, если 
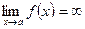. Функция называется бесконечно малой при 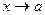или при 
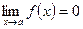, если 
или 
.
Теорема 1. Если функция бесконечно малая при 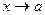(или при ) и 
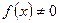для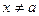 
из некоторой окрестности точки a, то функция 
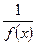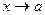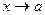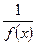бесконечно большая при (или при ). Верно обратное утверждение: если функция бесконечно большая при (или при ), то функция бесконечно малая при 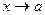(при ).
Теорема 2. Сумма двух бесконечно малых функций есть бесконечно малая функция.
Теорема 3. Произведение бесконечно малой функции на ограниченную функцию при 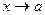(или при ) есть функция бесконечно малая.
Определение 3. Если 
, где , 
бесконечно малые при 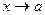, то и называются эквивалентными бесконечно малыми при (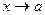 
~ 
).
Теорема. Пусть функции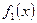 
, 
, 
, 
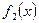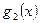бесконечно малые при 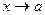. При этом 
~ 
, 
~ 
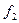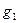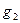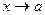при и 
. Тогда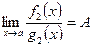 
.
Теоремы о пределах, связанные с арифметическими действиями
|
|
|
Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов, если последние существуют: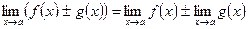 
.
Теорема 2. Предел произведения двух функций равен произведению их пределов, если последние существуют: 
.
Следствие. Постоянный множитель можно выносить за знак предела:
.
Теорема 3. Предел отношения двух функций равен отношению их пределов, если последние существуют, и предел знаменателя отличен от нуля: 
.
Пример 1. Найдите следующие пределы:
1) 
2) 
Замечательные пределы
Первый замечательный предел.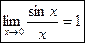 
~ 
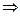
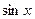при 
.
Следствия:
1) 
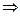
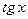~ при 2) 
~ 
при
3) 
~ при 4) 
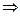
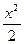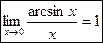
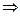
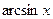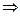
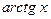~ при
Второй замечательный предел.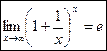 
или 
.
Следствия:
1) 
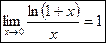
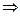
~ при . 2) 
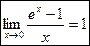
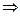
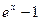~ при .
Пример 2. Найдите следующие пределы:
1) 
~ 
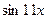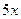при , 
~ 
при .
2) 
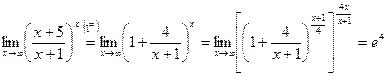
3) 
~ 
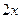при , 
~ 
при .
ОДНОСТОРОННИЕ ПРЕДЕЛЫ
Если при нахождении предела рассматривать значения x только слева от точки a, то такой предел называется левым или левосторонним и обозначается
.
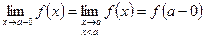а если рассматривать значения x только справа от точки a, то такой предел называется правым или правосторонним и обозначается
.
Из этих определений следует, что если существует предел
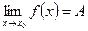, (1)
|
|
|
то существуют и односторонние пределы, причём
. (2)
Верно и обратное утверждение: если имеет место (2), то имеет место и (1).
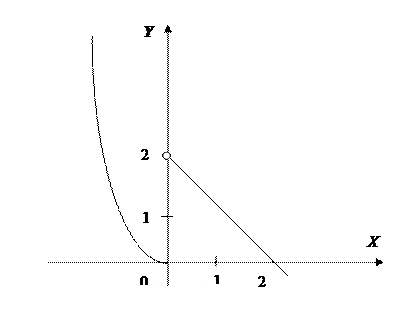
Пример:
Найти односторонние пределы функции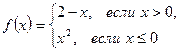 
в точке 
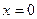. Существует ли у этой функции предел при ?
;
;
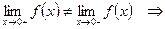
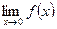- не существует.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ.
Дата добавления: 2022-07-02; просмотров: 15; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!