Властивості визначеного інтеграла

І. Якщо , то

ІІ. Сталий множник можна виносити з-під знака визначеного інтеграла, тобто

ІІІ. Якщо  та  інтегровні на [a; b], то

IV. Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл змінить лише свій знак на протилежний, тобто

V. Визначений інтеграл з однаковими межами інтегрування дорівнює нулю

VI. Якщо 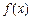 — інтегровна в будь-якому із проміжків: [a; b], [a; c], [с; b], то

VII. Якщо  і інтегровна для  то

VIII. Якщо 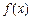, — інтегровні та  для  то

IX. Якщо f(x) — інтегровна та  для  то

Доведення випливає як наслідок із властивостей І та VIII.

Х. Теорема 7 (про середнє).

Якщо функція  — неперервна для  то знайдеться така точка  що:

                                       (2)

Геометричний зміст теореми про середнє полягає в тому, що існує прямокутник із сторонами  та b – a, який рівновеликий криволінійній трапеції аАВв за умови, що функція  та неперервна на проміжку [a; b] (рис. 3).

 

Рис. 3.

Поняття визначеного інтеграла зі змінною верхньою межею інтегрування, формула Ньютона—Лейбніца

Розглянемо інтеграл , який буде функцією від верхньої межі інтегрування. Змінній х надамо приросту , що зумовить приріст функції.

                    (рис. 4)

Рис. 4

Теорема 8. Якщо функція f(x) неперервна для будь-якого  то похідна від інтеграла зі змінною верхньою межею інтегрування по цій межі дорівнює підінтегральній функції від верхньої межі інтегрування, тобто

                                 (3)

Наслідки:

1. Визначений інтеграл зі змінною верхньою межею від функції 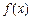 є одна із первісних для .

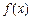2. Будь-яка неперервна функція на проміжку  має на цьому проміжку первісну, яку, наприклад, завжди можна побудувати у вигляді визначеного інтеграла зі змінною верхньою межею, тобто

Приклад. Знайти .

Функція — неперервна на проміжку  тому

Теорема 9. (Ньютона—Лейбніца). Якщо функція  — неперервна для  то визначений інтеграл від функції  на проміжку  дорівнює приросту первісної функції  на цьому проміжку, тобто

      де         (4)

Позначимо дію подвійної підстановки так:  тоді зв’язок між визначеним та невизначеним інтегралами можна подати такою рівністю:

  (5)

Наслідок.Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральних функцій і виконати над нею подвійну підстановку.

Приклад.

Метод підстановки у визначеному інтегралі

Теорема 10 . Якщо: 1)  — неперервна для ; 2)  3)  та  — неперервні для  4) при  то

                (6)

Зауваження. При заміні змінної інтегрування у визначеному інтегралі змінюються межі інтегрування, і тому нема потреби повертатись до початкової змінної.

Приклад.

=

Інтегрування частинами у визначеному інтегралі

Теорема 11 . Якщо функції  та  мають неперервні похідні для , то

                                          (7)

Приклад.

Формули наближеного обчисленнявизначених інтегралів

Визначений інтеграл від заданої неперервної функції далеко не завжди можна легко та точно обчислити. Однак, використовуючи геометричний зміст, можна побудувати ряд наближених формул, за допомогою яких інтеграл обчислюється з будь-якою точністю. Розглянемо такі формули.

Нехай від заданої та неперервної на  функції  треба обчислити визначений інтеграл

Поділимо  точками а = х₀, х₁, х₂, ..., х_n–1, x_n = b на n рівних частин завдовжки .

Значення функції 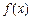 у точках позначимо так: ,  Побудуємо для функції  на проміжку  інтегральні суми, кожна з яких буде наближено подавати визначений інтеграл:

                            (8)

                            (9)

Формули (8) та (9) називаються формулами лівого та правого прямокутників відповідно. Ця назва пов’язана з тим, що криволінійна трапеція наближено замінюється відповідною ступінчастою фігурою (рис. 5).

    Рис. 5

ІІ. Формула трапецій.

Більш точне значення визначеного інтеграла буде, якщо криву  замінювати не ступінчастою лінією, а вписаною ламаною, тобто криволінійна трапеція замінюється сумою n прямолінійних трапецій (рис. 7.9). У цьому разі наближене значення інтеграла можна дістати як середнє арифметичне значень, обчислених за формулами (8) та (9).

                   (10)

Рис. 6

 

 

ІІІ. Формула Сімпсона.

Поділимо  на парне число рівних частин  точками  так, що а = х₀, b = x_2m. На кожному із цих проміжків криволінійну сторону трапеції, рівнянням якої є ,

                       Рис. 7

замінюємо певною параболою. Таке наближення для обчислення визначеного інтеграла буде точнішим, ніж за попередніми формулами (рис. 7).

        (11)

---

Дата добавления: 2022-01-22; просмотров: 20; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!