Варианты для заданий № 5, №6, №7.
Даны точки А, В, С, D.
| № варианта | А | В | С | D |
| 1 | (2;-1;3) | (-1;3;2) | (0;1;-1) | (-1;-3;1) |
| 2 | (-2;-1;3) | (1;3;-2) | (3;1;-1) | (2;-3;-2) |
| 3 | (0;-1;3) | (-2;3;-1) | (0;1;-1) | (-1;-3;1) |
| 4 | (3;-2;3) | (-1;0;2) | (-3;1;-1) | (-3;-3;1) |
| 5 | (1;-1-2) | (-1;2;-2) | (2;1;-2) | (-1;-2;3) |
| 6 | (1;-1;3) | (-1;-2;2) | (1;1;-1) | (0;-3;1) |
| 7 | (2;-2;3) | (-2;3;2) | (1;1;-1) | (-1;-3;0) |
| 8 | (-2;1;-3) | (2;3;2) | (3;-1;-1) | (-1;-3;1) |
| 9 | (-1;-1;3) | (-1;3;-2) | (-3;1;-1) | (-1;-3;2) |
| 10 | (2;-1;2) | (-1;-3;2) | (2;1;-1) | (-1;-3;0) |
Задание 5.
Найти:
1) направляющие косинусы вектора 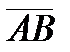 .
.
Найдем координаты вектора 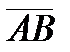 . Для этого из координат конца вектора (т.е. координат точки В(1;3;-2)) вычитаем координаты начала (т.е. координат точки А(-2;-1;3)).
. Для этого из координат конца вектора (т.е. координат точки В(1;3;-2)) вычитаем координаты начала (т.е. координат точки А(-2;-1;3)).
 = (1-(- 2); 3-(-1); 2-3) =(3; 4; -1)
= (1-(- 2); 3-(-1); 2-3) =(3; 4; -1)
Обозначим первую координату вектора  через
через  , вторую- через
, вторую- через  , третью – через
, третью – через  , т.е.
, т.е.
 =(
=(  ) =(3; 4; -1).
) =(3; 4; -1).
Тогда направляющие косинусы вычисляются по формулам (координата вектора делится на его длину):
cos a =  ; cos b =
; cos b = 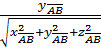 ; cos g =
; cos g =  .
.
То есть
cos a = 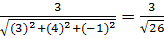 ; cos b =
; cos b =  ;
;
cos g =  .
.
2) проекцию вектора 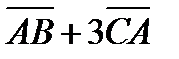 на вектор
на вектор  , т.е. пр
, т.е. пр 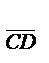
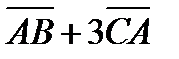 .
.
Чтобы найти проекцию вектора 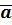 на вектор
на вектор  , надо скалярное произведение этих векторов разделить на длину вектора
, надо скалярное произведение этих векторов разделить на длину вектора  .
.
пр 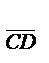
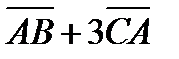 =
=  .
.
Найдем координаты векторов, используемых в задании.
 = (3; 4; -1)
= (3; 4; -1) 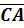 = (-5; -2;4), 3
= (-5; -2;4), 3  = (-15; -6; 12)
= (-15; -6; 12)
 =(3-15; 4- 6; -1+12) = (-7; -2; 11),
=(3-15; 4- 6; -1+12) = (-7; -2; 11), 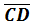 = (5; -4; 1).
= (5; -4; 1).
Тогда
пр 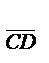
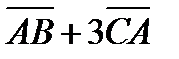 =
= 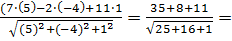

3) высоту h пирамиды АВСD, опущенную из вершины D на плоскость основания АВС.
Высота h треугольной пирамиды АВСD равна  -объем пирамиды разделить на площадь основания
-объем пирамиды разделить на площадь основания  –площадь основания.
–площадь основания.
|
|
|
SDABC =  |
| 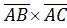 |.
|.
Найдем векторное произведение векторов  и
и 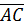 .
.
 =
=  =
=  -
- 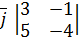 +
+ 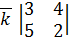 = -14
= -14  -7
-7 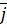 - 14
- 14 
Модуль векторного произведения равен площади параллелограмма, построенного на этих векторах, тогда площадь треугольника, лежащего в основании пирамиды, вычисляется следующим образом:
SDABC = 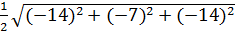 =
=  =
=  ед2.
ед2.
Найдем объем пирамиды.
Объем пирамиды равен  объему параллелепипеда, численно совпадающим со смешанным произведением трех векторов, являющихся сторонами параллелепипеда.
объему параллелепипеда, численно совпадающим со смешанным произведением трех векторов, являющихся сторонами параллелепипеда.
 = (3;4;-1)
= (3;4;-1)  = (5; 2; -4)
= (5; 2; -4)  = (4; -2; -5)
= (4; -2; -5)
 =
= 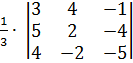 =
=  |-30 +10 – 64 + 8 – 24 +100 | =
|-30 +10 – 64 + 8 – 24 +100 | = 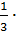 10 ед3
10 ед3
SDABC =  ед2
ед2
 =
= 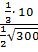 =
= 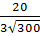 .
.
Задание 6.
Доказать, что вектора  образуют базис. Найти разложение вектора
образуют базис. Найти разложение вектора  в этом базисе.
в этом базисе.
Найдем координаты векторов.
 = (3;4;-1)
= (3;4;-1) 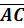 = (5; 2; -4)
= (5; 2; -4)  = (4; -2; -5)
= (4; -2; -5)  = (5; -4; 1).
= (5; -4; 1).
Убедимся, что вектора  образуют базис. Вектора образуют базис, если они линейно независимы, то есть определитель, элементами которого являются координаты векторов, не равен нулю.
образуют базис. Вектора образуют базис, если они линейно независимы, то есть определитель, элементами которого являются координаты векторов, не равен нулю.
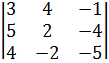 = -30 +10 – 64 + 8 – 24 +100 =10 ¹ 0.
= -30 +10 – 64 + 8 – 24 +100 =10 ¹ 0.
Т.е. вектора линейно независимы, следовательно, вектора  образуют базис и следовательно, вектор
образуют базис и следовательно, вектор  будет иметь следующее разложение:
будет иметь следующее разложение:
 =
= 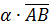 +b ·
+b · 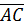 +g ·
+g ·  .
.
Подставим вместо векторов их координаты:

Используя операции умножения вектора на число и сложение векторов, получим систему
|
|
|

Решаем систему методом Гаусса.
 ~
~ 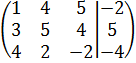 ~
~  ~
~ 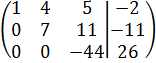
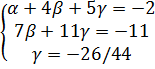 =>
=> 
 =443/154
=443/154  -13/33
-13/33  -9/14
-9/14  .
.
Задание 7.
1) Составить уравнение прямой L , проходящих через две точки A и B
A = (-2;-1;3); B= (1;3;2); C = (3;1;-1); D = (2;-3;-2)
1) Дано:
A(-2;-1;3); B(1;3;2),
АÎL, BÎL
Найти
L .
Решение.
1.Нарисуем чертеж к задаче.
А
М(х,у,z)
В
2. На объекте исследования, т.е прямой А B, выберем произвольную точку М с текущими координатами, т.е М(  ).
).
3. Построим вектора: один вектор с началом в заданной точке и концом в точке М , т.е  и вектор, соединяющий две заданных точки т.е
и вектор, соединяющий две заданных точки т.е  .
.
4. Найдем координаты этих векторов.
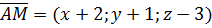 ,
,  = (3;4;-1).
= (3;4;-1).
5. Выясним, как расположены вектора относительно друг друга. Они параллельны  ||
||  , следовательно, их координаты пропорциональны.
, следовательно, их координаты пропорциональны.
 .
.
Таким образом, получили каноническое уравнение прямой.
2) написать параметрическое уравнение прямой L 1 , проходящей через точку С, параллельно прямой AB ;
Дано:
A = (-2;-1;3); B= (1;3;2); C = (3;1;-1)
L:  (см. предыдущую задачу)
(см. предыдущую задачу)
СÎ L1
Найти
L1.
Решение
1.Нарисуем чертеж к задаче.
| А |
| В |
| C |
| L1 |
| M(x,y,z) |
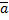
|
2. На объекте исследования, т.е прямой L1, выберем произвольную точку М с текущими координатами М(  ).
).
3. Построим вектора: один вектор с началом в заданной точке С и концом в точке М , т.е  , лежащий на прямой L1 и направляющий вектор (вектор параллельный прямой)
, лежащий на прямой L1 и направляющий вектор (вектор параллельный прямой)  = (3, 4, -1), найденный из канонического уравнения прямой AB:
= (3, 4, -1), найденный из канонического уравнения прямой AB:  .
.
|
|
|
4. Найдем координаты этих векторов.
 ;
;  = (3, 4, -1).
= (3, 4, -1).
5. Выясним, как расположены вектора относительно друг друга. Они параллельны  ||
|| 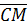 , следовательно, их координаты пропорциональны.
, следовательно, их координаты пропорциональны.
Таким образом, получили 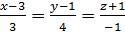 -это каноническое уравнение прямой L1.
-это каноническое уравнение прямой L1.
3) написать уравнение высоты DH треугольной пирамиды ABCD ;
Дано: A(2;-2;3); B(-2;3;2); C(1;1;-1); D(-1;-3;0)
DH ^ AB C
Найти DH
Решение
Будем решать задачу в два этапа.
1) Найдем уравнение плоскости, проходящей чрез точки A,B и C .
1.Нарисуем чертеж.
| A |
| B |
| M(x,y,z) |
| Р |
| C |
2. На объекте исследования, т.е плоскости Р, выберем произвольную точку М с текущими координатами М(  ).
).
3. Построим вектора: один вектор с началом в заданной точке А и концом в точке М , т.е  , второй вектор, соединяющий две заданных точки
, второй вектор, соединяющий две заданных точки  и третий вектор, соединяющий две заданных точки
и третий вектор, соединяющий две заданных точки 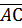 .
.
4. Найдем координаты этих векторов.
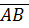 = (-4;5;-1)
= (-4;5;-1)  = (-1; 3;-4)
= (-1; 3;-4) 
5. Выясним, как расположены вектора относительно друг друга. Эти вектора лежат в одной плоскости, следовательно, их смешанное произведение равно нулю т.е.
|
|
|
 ×
× 
Раскроем скобки.
-17x - 15y - 7z + 25= 0 –это уравнение плоскости АВС.
2) Найдем уравнение высоты DH.
1.Нарисуем чертеж.
| A |
| B |
| M(x,y,z) |

|
| C |
| D |
| Н |
2. На объекте исследования, т.е прямой DH, выберем произвольную точку М с текущими координатами М(  ).
).
3. Построим вектора: один вектор с началом в заданной точке D и концом в точке М , т.е  и другой вектор- вектор нормали (вектор перпендикулярный плоскости)
и другой вектор- вектор нормали (вектор перпендикулярный плоскости)  .
.
4. Найдем координаты этих векторов.
Из уравнения плоскости -17x - 15y - 7z + 25= 0 найдем координаты вектора нормали к плоскости (это коэффициенты при неизвестных)  =(-17; -15; -7);
=(-17; -15; -7); 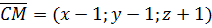
5. Выясним, как расположены вектора относительно друг друга. Вектора  и
и 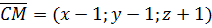 параллельны, следовательно, их координаты пропорциональны:
параллельны, следовательно, их координаты пропорциональны:
 -это и есть искомое уравнение высоты DH.
-это и есть искомое уравнение высоты DH.
4) написать уравнение медианы AD треугольника ABC ;
Дано:
A(2;-2;3); B(-2;3;2); C(1;1;-1); D(-1;-3;0)
D1ÎBC; | BD1| = |D1C|
Найти AD1.
Решение
Координаты точки D1 находим как половина суммы координат точек С и В.
D1 = 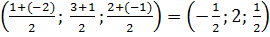
Строим каноническое уравнение прямой аналогично задания 1)
AD1:  =>
=> 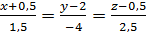
5) определить угол между плоскостями ABC и ACD ;
6) Дано:
A(2;-2;3); B(-2;3;2); C(1;1;-1); D(-1;-3;0)
-17x - 15y - 7z + 25= 0 –уравнение плоскости АВС.
Найти j .
Решение
Найдем плоскость ACD (аналогично нахождению плоскости АВС)
Три вектора  = (-3;-1;-3)
= (-3;-1;-3)  = (-1; 3; -4)
= (-1; 3; -4) 
Лежат в одной плоскости, следовательно их смешанное произведение равно нулю т.е.
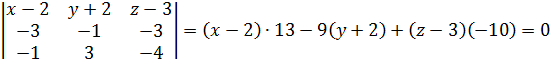 =>
=>
13х -9y -10z-14 = 0 –это уравнение плоскости ACD.
Угол между двумя плоскостями то же самое, что угол между их векторами нормали.
Вектор нормали плоскости ABC  = (-17; -15; -7), а вектор нормали плоскости ACD
= (-17; -15; -7), а вектор нормали плоскости ACD  = (13; -9; -10)
= (13; -9; -10)
cos  =
=  =
= 
j =arcos (  )
)
Задание 8.
Определить тип кривой второго порядка; найти координаты центра; полуоси.
х2 - 4у2 – 6х - 16у - 29 = 0/
Сгруппируем слагаемые, содержащие х и слагаемые, содержащие у.
(х2 – 6х) -4(у2 + 4у) -29 = 0
Выделим полный квадрат относительно х и у.
(х2 – 6х +9 – 9) -4(у2 + 4у +4- 4) -29 = 0.
Свернем квадрат разности относительно х и квадрат суммы относительно у.
(x - 3)2 -4(y +2)2 +16 -9 -29 =0
(x - 3)2 -4(y +2)2 = 22.
Разделим правую и левую части уравнения на 22.

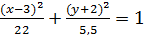 .
.
Это уравнение эллипса, центр которого имеет координаты (3;-2), большая полуось равна 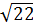 , малая
, малая  .
.
Варианты к заданию № 8.
1. 5х2 + 9у2 – 30х + 18у + 9 = 0
2. 16х2 - 9у2 – 64х - 54у - 161 = 0
3. 4х2 + 9у2 – 16х - 18у - 11 = 0
4. х2 - 4у2 – 6х + 16у - 11 = 0
5. 16х2 + 25у2 + 32х - 100у - 284 = 0
6. 9х2 - 16у2 + 90х + 32у - 367 = 0
7. х2 - 4у2 – 6х - 16у - 29 = 0
8. 4х2 + 3у2 – 8х + 12у - 32 = 0
9. 16х2 - 9у2 – 64х - 18у + 199 = 0
Задание 9. Возвести комплексное число  в степень:
в степень:
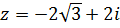 , z4 - ?
, z4 - ?
Найдем модуль и аргумент комплексного числа z = x + iy
Модуль:  =
=  = 4
= 4
Аргумент, т.е. угол: 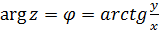 =
= 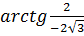 =
=  = p -
= p -  =
= 
Для z1= z4 модуль будет r1 = r4 = 44 = 256, а аргумент j1 = 4j = 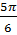 ·4
·4  .
.
Таким образом z4 =256·( cos  + i · sin
+ i · sin  )
)
Варианты к заданию № 9.
1)  , ,  ; ;
| 3)  , ,  ; ;
|
2)  , , 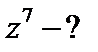 ; ;
| 4)  , ,  ; ;
|
5) 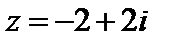 , ,  ; ;
| 8)  , , 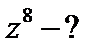 ; ;
|
6)  , ,  ; ;
| 9) 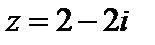 , ,  ; ;
|
7)  , , 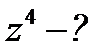 ; ;
| 10)  , , 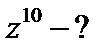 . .
|
Приложение 1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Дата добавления: 2022-01-22; просмотров: 26; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
