Технические средства обучения и контроля, использование ЭВМ
a. Система тестирования «ЦДО -тест», разработка ДГТУ.
b. Сайт Центра дистанционного обучения http:// de.dstu.ru
c. Сайт www.politech-tag.ru
Литература
Карта методического обеспечения дисциплины
| № | Автор | Название | Издательство | Год издания |
| 1 | 2 | 3 | 4 | 5 |
| 6.1.1 | Шевченко Н.П. | Алгебра и аналитическая геометрия | ДГТУ. - Ростов н/Д | 2006 |
| 6.1.2 | Зубков А.Н., Павлова М.Н | Матрицы и их применение. Линейные преобразования. | ДГТУ - Ростов н/Д | 2012 |
| 6.1.3 | Данко П.Е. | Высшая математика в упражнениях и задачах. Ч.1 | М. : ОНИКС 21 век: Мир и Образование | 2004 |
| 6.1.4 | Ворович Е.И. | Учебно-методическое пособие по подготовке к интернет экзамену | ДГТУ. - Ростов н/Д | 2007 |
| 6.1.5 | Шипачев В.С. | Задачник по высшей математике | М. : Высш. шк. | 2005 |
| 6.6.1 | Абуев Ф.Л. | Программа и варианты контрольных работ для студентов первого курса заочного факультета | ДГТУ. - Ростов н/Д | 2006 |
| 6.6.2 | Шевченко Н.П. | Программа, варианты и методические указания к контрольным работам для студентов второго курса заочного факультета | ДГТУ. - Ростов н/Д | 2007 |
Вариант контрольной работы соответствует последней цифре номера зачетной книжки (нуль соответствует варианту №10)
Образец титульного листа см. приложение 1
Задание, выполненное в печатном виде, требуется помещать в рамку (см. образец в приложении 2). Задание, выполненное в тетради, не требуется помещать в рамку.
|
|
|
Контрольная работа №1
Задание №1
Вычислить А2 - 3АВ, где
А =  В =
В = 
Решение. Находим матрицу
А2 =А∙А =  ∙
∙  .
.
Для получения элемента , стоящего в первой строке и в первом столбце, перемножим соответствующие элементы первой строки матрицы А и элементы первого столбца матрицы В (т.е первый элемент первой строки матрицы А умножим на первый элемент первого столбца матрицы В; второй элемент первой строки матрицы А на второй элемент первого столбца матрицы В; третий элемент первой строки матрицы А умножим на третий элемент первого столбца матрицы В)и их произведения сложим. Для получения элемента , стоящего в первой строке и во втором столбце, перемножим соответствующие элементы первой строки матрицы А и элементы второго столбца матрицы В и их произведения сложим и т. д. То есть для получения элемента , стоящего в i-ой строке и в j-ом столбце, перемножим соответствующие элементы j-го строки матрицы А и элементы j-го столбца матрицы В (т.е первый элемент i-ой строки матрицы А умножим на первый элемент j-го столбца матрицы В; второй элемент i-ой строки матрицы А на второй элемент j-го столбца матрицы В; третий элемент i-ой строки матрицы А умножим на третий элемент j-го столбца матрицы В)и их произведения сложим. и т.д. В итоге получим матрицу размером 3×3:
|
|
|
А2 = 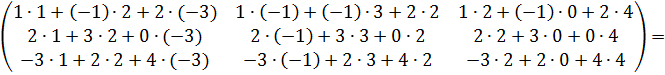
= 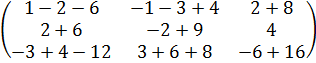 =
= 
Аналогично находим матрицу  :
:
А∙В =  ∙
∙  =
=
= 
= 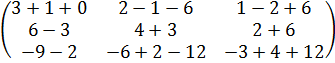 =
= 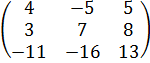
Вычисляем затем матрицу
3∙А∙В = 3∙ 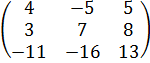 =
=
(Чтобы умножить матрицу на число, надо каждый элемент этой матрицы умножить на это число.)
=  .
.
Таким образом, получим, что матрица
А2 - 3АВ =  -
-  =
=
(Чтобы сложить две матрицы, надо сложить их соответствующие элементы.)
=  .
.
Варианты задания № 1
1.Даны матрицы А =  и В =
и В =  .
.
Вычислить ВА+2В.
2.Даны матрицы А = 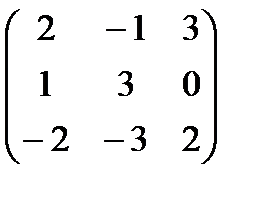 и В =
и В =  .
.
Вычислить АВ-3В.
3.Даны матрицы А =  и В =
и В =  .
.
Вычислить АВ-3А.
4.Даны матрицы А =  и В =
и В =  .
.
Вычислить 3В + ВА.
5.Даны матрицы А =  и В =
и В =  .
.
Вычислить 2А + ВА.
6.Даны матрицы А = 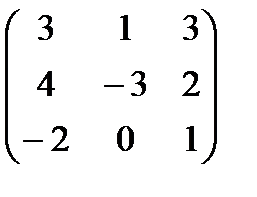 и В =
и В = 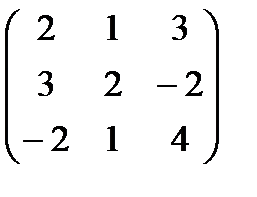 .
.
Вычислить 3В + ВА.
7.Даны матрицы А =  и В =
и В =  .
.
Вычислить 2В + 3ВА.
8.Даны матрицы А =  и В =
и В =  .
.
Вычислить 3В +2 АВ.
9.Даны матрицы А =  и В =
и В =  .
.
Вычислить 3В + ВА.
10.Даны матрицы А =  и В =
и В =  .
.
Вычислить 4А + ВА.
Задание №2
Решить системы линейных алгебраических уравнений матричным способом.
Запишем систему (1)
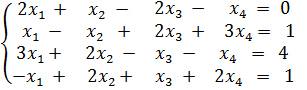 .
.
через произведение матриц по формуле (2.3). Для этого составим матрицу, соответствующую данной системе:
А =  ,
,
столбец свободных членов В =  и столбец неизвестных Х =
и столбец неизвестных Х =  .
.
|
|
|
Тогда система уравнений запишется в матричном виде
 ∙
∙  =
=  ,
,
т.е. А∙Х =В .Откуда находим,что Х = А-1∙В.
Найдем обратную матрицу А-1. Для этого
1) вычислим главный определитель матрицы
 =
=  =(С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
=(С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
=  = 1∙(-1)2+1
= 1∙(-1)2+1 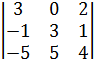 +0+0+0 =
+0+0+0 =
= -  = - (3∙(3∙4 -1∙5)+0 +
= - (3∙(3∙4 -1∙5)+0 +
2∙ (-1∙5- 3∙(-5)) = - ( 3∙7+2∙10)= - 41.
2) построим матрицу (  ij ) из алгебраических дополнений
ij ) из алгебраических дополнений  ij элементов матрицы А.
ij элементов матрицы А.
Найдем эти алгебраические дополнения (определители вычисляем по правилу треугольника):
 11 = (-1)1+1 ∙
11 = (-1)1+1 ∙  = 2 - 4 +6+6-1-8 = 1,
= 2 - 4 +6+6-1-8 = 1,
 12 = (-1)1+2 ∙
12 = (-1)1+2 ∙  = -(-2 + 2 +9 - 3+1- 12) = 5,
= -(-2 + 2 +9 - 3+1- 12) = 5,
 13 = (-1)4 ∙
13 = (-1)4 ∙  = 4 - 1 + 18+6 +2+6 = 35,
= 4 - 1 + 18+6 +2+6 = 35,
 14 = (-1)5 ∙
14 = (-1)5 ∙  = -(2 - 1 + 12+ 4+2 + 3 ) = -22,
= -(2 - 1 + 12+ 4+2 + 3 ) = -22,
 21 = (-1)3 ∙
21 = (-1)3 ∙  = -(-2 + 4 - 2- 2+1+ 8) = -7,
= -(-2 + 4 - 2- 2+1+ 8) = -7,
 22 = (-1)4 ∙
22 = (-1)4 ∙  = -4 - 2 - 3+ 1+2+ 12 = 6,
= -4 - 2 - 3+ 1+2+ 12 = 6,
 23 = (-1)5 ∙
23 = (-1)5 ∙  =-(8 - 6 + 1- 2 + 4- 6 ) = 1,
=-(8 - 6 + 1- 2 + 4- 6 ) = 1,
 24 = (-1)6 ∙
24 = (-1)6 ∙  = 4 + 1 – 12 – 4 + 4- 3 = -10,
= 4 + 1 – 12 – 4 + 4- 3 = -10,
 31 = (-1)4 ∙
31 = (-1)4 ∙ 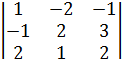 = 4 - 12 +1+4-4-3 = -10,
= 4 - 12 +1+4-4-3 = -10,
 32 = (-1)5 ∙
32 = (-1)5 ∙  = -(8 - 1 +6 - 2- 6+ 4) = -9,
= -(8 - 1 +6 - 2- 6+ 4) = -9,
 33 = (-1)3+3 ∙
33 = (-1)3+3 ∙  = -4 - 3 - 2+ 1- 12- 2 = -22,
= -4 - 3 - 2+ 1- 12- 2 = -22,
 34 = (-1)7 ∙
34 = (-1)7 ∙ 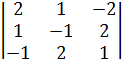 = -(-2 - 2 - 4+ 2-8- 1) = 15,
= -(-2 - 2 - 4+ 2-8- 1) = 15,
 41 = (-1)5 ∙
41 = (-1)5 ∙ 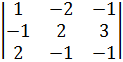 = -(-2 - 1 – 12 +4 + 3 + 2) = 6,
= -(-2 - 1 – 12 +4 + 3 + 2) = 6,
 42 = (-1)6 ∙
42 = (-1)6 ∙  = -4 – 18 + 1+6 + 6- 2 = -11,
= -4 – 18 + 1+6 + 6- 2 = -11,
 43 = (-1)7 ∙
43 = (-1)7 ∙  = -(2 - 2 + 9 - 3-12 +1 ) = 5 ,
= -(2 - 2 + 9 - 3-12 +1 ) = 5 ,
 44 = (-1)8 ∙
44 = (-1)8 ∙ 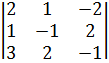 = 2- 4 +6 - 6- 8+ 1 = -9.
= 2- 4 +6 - 6- 8+ 1 = -9.
Полчили матрицу
(  ij ) =
ij ) =  .
.
3) Находим присоединённую матрицу (  ji )= (
ji )= (  ij )T :
ij )T :
(  ji ) =
ji ) =  .
.
4) Получаем по формуле (2.2) обратную матрицу
|
|
|
А-1 =  =
=  ∙
∙  =
=
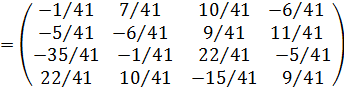
Тогда
Х =  ∙
∙ 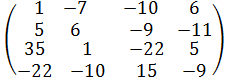 ∙
∙  =
=
= 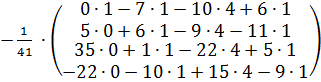 =
=  = =
= =  =
=  .
.
Ответ:  .
.
Рассмотрим второй способ получения обратной матрицы А-1 .
Используется формула вида (9.9):
 ,
,
где Е – единичная матрица; А – заданная матрица;  - обратная матрица.
- обратная матрица.

С1 С2

С2 := -2∙С1 + С2,

С3 := -3∙С1 + С3, С4 := С1 + С4,

С4 С2

С1 := С2 + С1, С3 := -5∙С2 + С3, С4 := -3С2 + С4,

С1 := 5С3 + 22С1, С2 := 3∙С3 + 22С2, С4 :=- 15∙С3 +22∙ С4,

С1 :=- С4 +41С1, С2 := -5∙С4 + 41С2, С3 :=35∙С4 +41∙ С3

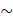
Разделив первую и вторую строки матрицы на 902, третью на -902.а четвертую на 41, получим
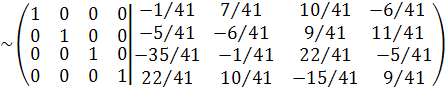
 ,
,
А-1 =  .
.
Варианты задания №2
Решить системы линейных алгебраических уравнений методом Гаусса и матричным способом.
1.  6.
6. 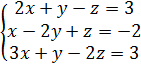
2. 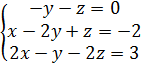 7.
7. 
3.  8.
8. 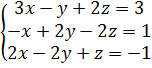
4. 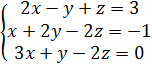 9.
9. 
5. 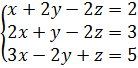 10.
10. 
Задание №3
Решить систему линейных алгебраических уравнений
методом Гаусса;
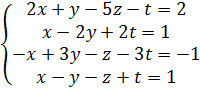 .
.
Решение. Составим расширенную матрицу и приведем ее с помощью элементарных преобразований к треугольному виду.
 С2 С1
С2 С1 
С2 := -2∙С1 + С2, С3 := С1 + С3, С4 := -С1 + С4


С3 := -5С2 + С3, С4 := -С1 + С4

Разделим третью строку на 14, а четвертую на 4
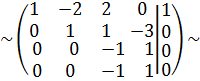 С4 := -С3 + С4
С4 := -С3 + С4 
Составим по полученной матрице систему уравнений
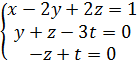 или
или  либо
либо 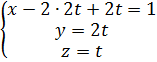 .
.
Таким образом, имеем  .
.
Обозначим t = С. Тогда система имеет множество решений :
 . При С = 1 получим ФСР, т.е.
. При С = 1 получим ФСР, т.е.

или 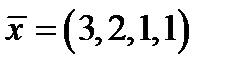 .
.
Варианты задания №3
1.  2.
2. 
3.  4.
4. 
5. 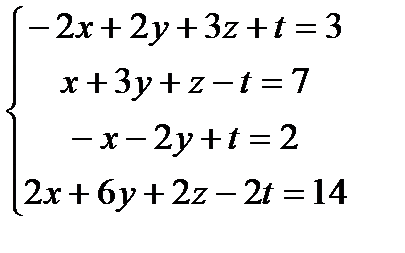 6.
6. 
7.  8.
8. 
9. 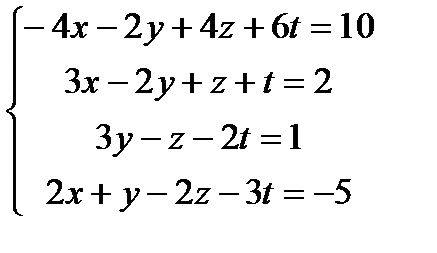 10.
10. 
Задание №4
Найти собственные числа и собственные векторы матрицы А.

Решение. Запишем характеристическое уравнение:
Определение2.11. Вектор Х ≠ 0 п-голинейного пространства ( т.е. имеет п координат) удовлетворяющий равенству  , называется собственным вектором, а соответствующее ему число
, называется собственным вектором, а соответствующее ему число  -собственным значением (характеристическим числом) матрицыА.
-собственным значением (характеристическим числом) матрицыА.
где А – матрица размером п×п , а 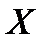 -вектор-столбец, имеющий п координат. Используя единичную матрицу Е, соотношение
-вектор-столбец, имеющий п координат. Используя единичную матрицу Е, соотношение  можно записать в виде
можно записать в виде
(А- l Е ) × Х = 0 если перенести l Х в левую сторону.
(А- l Е ) × Х = 0 - это однородная линейная система уравнений (ОСЛУ). Она будет иметь не нулевое решение если определитель | (А- l Е ) | =0. Построим такой определитель для нашего примера
 .
.
Вычисляя определитель по правилу: произведение элементов ,стоящих на главной диагонали минус произведение элементов, стоящих на побочной диагонали получим:
 . Раскрыв скобки и приведя подобные слагаемые, получим квадратное уравнение
. Раскрыв скобки и приведя подобные слагаемые, получим квадратное уравнение
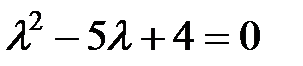 .
.
Находим его корни  ,
,  . Найдем собственные векторы
. Найдем собственные векторы 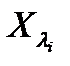 и
и  , отвечающие соответственным этим собственным числам. Для этого рассмотрим ОСЛАУ:
, отвечающие соответственным этим собственным числам. Для этого рассмотрим ОСЛАУ:
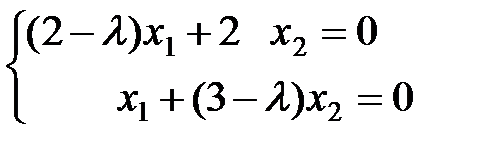 .
.
Вычислим ОСЛАУ при  . Тогда получаем систему
. Тогда получаем систему
 .
.
Выразим одну из переменных через другую:  . Полагая
. Полагая 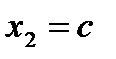 , получим
, получим 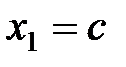 , и потому
, и потому
 .
.
Придавая различные значения параметру с, получим собственные векторы, соответствующие собственному числу 
Найти собственные числа и собственные векторы матрицы

Решение. Запишем характеристическое уравнение:

или, вычисляя определитель, получим:
 , т.е.
, т.е.
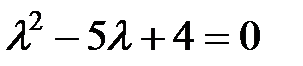 .
.
Находим его корни  ,
,  . Найдем собственные векторы
. Найдем собственные векторы 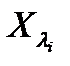 и
и  , отвечающие соответственным этим собственным числам. Для этого рассмотрим ОСЛАУ:
, отвечающие соответственным этим собственным числам. Для этого рассмотрим ОСЛАУ:
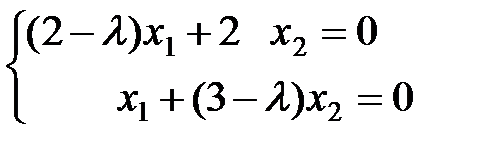 .
.
Вычислим ОСЛАУ при  . Тогда получаем систему
. Тогда получаем систему
 .
.
Выразим одну из переменных через другую:  .Полагая
.Полагая 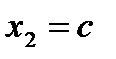 , получим
, получим 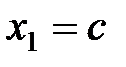 , и потому
, и потому
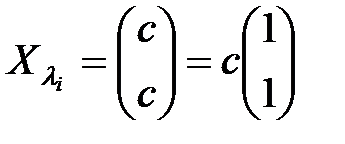 .
.
Придавая различные значения параметру с получим собственные векторы, соответствующие собственному числу 
Варианты задания №4
1.  2.
2. 
3.  4.
4. 
5. 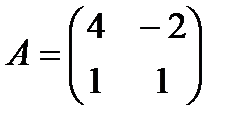 6.
6. 
7. 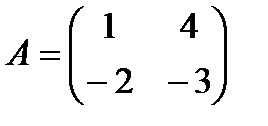 8.
8. 
9.  10.
10.  .
.
Дата добавления: 2022-01-22; просмотров: 20; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
