Применение производной к исследованию функций.

Признак возрастания (убывания) функции

 

 I) Повтори материал: 

 

1) Определение: Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции.

Пусть произвольная кривая линия- это график функции у =f(x), тогда символическая запись определения возрастающей функции имеет вид: 

x₂>x₁

f(x₂)>f(x₁)

 

2) Определение: Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции. 

Символическая запись определения убывающей функции имеет вид:

х₂>x₁

f(x₂)<f(x₁)

 

3) Определение приращения функции и приращения аргумента:

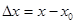 - приращение аргумента.

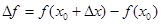- приращение функции.

 

4) Определение производной:

 

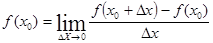
Пусть на дана какая-то функция у = f(x). Возьмем систему координат и проведем произвольную кривую линию.

Представим график. Возьмем на оси ОХ произвольное значение х₀ и найдем графически соответствующее ему значение функции f( x₀).

Возьмем новое значение аргумента  и найдем для него соответствующее значение функции .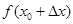

Сравним между собой значения аргумента и соответствующее значение функций.

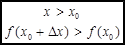
- получим символическую запись определения возрастающей функции.

 

Перенесем её в левую часть.

 

Получим, что в определении производной

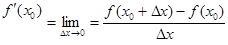 числитель и знаменатель оба положительные (>0), а значит, и сама производная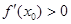  

Вывод: Если производная , то функция будет возрастающей.

 

Аналогично рассматривается случай для убывающей функции. y= f(x)

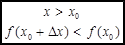 - получим символическую запись определения убывающей функции.

Переносим все в левую часть:

.

Получим, что в определении производной 

знаменатель положительный, а числитель отрицательный. Значит сама производная .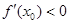

Вывод: Если производная отрицательная, т.е.  , то функция будет убывающей.

Как возрастающие, так и убывающие функции называются монотонными.

 

Правило нахождения интервалов монотонности

1. Найти нули и точки разрыва f ’(x);

2. Определить методом проб знак f ’(x) в интервалах, на которые полученные в п.1 точки делят область определения функции f (x);

3. Интервалы в которых f ’(x) > 0, являются интервалами возрастания функции, а интервалы в которых f ’(x) < 0, - интервалами убывания функции. При этом если на двух соседних интервалах, граничная точка которых является нулем производной f ’(x), знак f ’(x) одинаков, то они составляют единичный интервал монотонности.

Пример 3.

Найти промежутки возрастания и убывания функции:

 

 

Приравняем производную к нулю:

 

 

Отметим полученные числа 1 и -3 на числовой прямой. Эти точки разобьют числовую прямую на интервалы.

 

Определим знак производной на каждом интервале. Для этого из каждого интервала возьмем число и подставим его производную

 

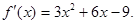
Возьмем из крайнего левого интервала число -4.

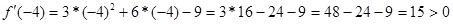
получим число положительное, поэтому в интервале

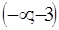поставим знак +. Аналогично определяем знак производной на двух других интервалах.

 

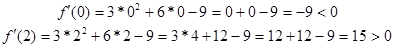
Ответ: функция возрастает на  убывает на (-3;1).

 

Экстремум функции:  Максимумы и минимумы

 

Пусть нам дана какая-то функция у=f(x).

Проведем произвольную кривую линию и будем считать, что это график нашей функции.

Мы видим, что слева от точки х₁ функция возрастает, поэтому производная имеет знак + (отметим его на чертеже). От точки х₁ до точки х₂ функция убывает, поэтому производная имеет знак минус -. Аналогично расставим знаки производной на других промежутках. Рассмотрим, например, точку х₁.

 

Слева от этой точки производная имеет знак плюс +, а справа знак минус -.

- А какой знак имеет производная в самой точке х₁?

- В самой точке х₁ производная не имеет никакого знака, в данном случае производная в точке х₁ равна нулю, т.е. это граница между положительными и отрицательными числами.

Но производная может не иметь никакого знака в точке и в случае если она в этой точке не существует.

Определение. Точки, в которых производная равна нулю или не существует, называются критическими.

 

Из графика видно, что при переходе через критические точки производная может менять знак с + на -, а может наоборот с – на +.

 

Определение. Точка х = х₀ называется точкой максимума ( минимума) функции y = f(x), если существует такая окрестность точки х₀, что для всех х (х  х₀) этой окрестности выполняется неравенство:

f(x) < f(x₀), [f(x) > f(x₀)].

 

Определение. Точками максимума и минимума функции называются точками ее экстремума, а значение функции в точке максимума ( минимума) - максимумом ( минимумом) или экстремумом функции.

 

Определение. Если при переходе через критическую точку производная меняет знак с + на -, то это будет точка

максимума (обозначается х_max). А если с – на +, то точка минимума ( x_min). 

 Вместе точки максимума и минимума называются экстремумы  .

 

---

Дата добавления: 2021-12-10; просмотров: 37; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!