Приближенное решение алгебраических и трансцендентных уравнений
Для решения уравнений, значения корней которых определить аналитическим путем невозможно, применяются численные методы, позволяющие получить не точное, а приближенное решение уравнения, но с любой степенью точности, обеспечиваемой компьютером. Большинство численных методов решения уравнения являются итерационными. Это означает, что отдельный шаг (или итерация) алгоритма позволяет получить лишь очередное приближение к значению корня, однако каждая последующая итерация позволяет получить все более и более точные значения корня, пока требуемая точность не будет достигнута.
Постановка задачи
Дано уравнение f(x)=0, х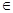 
[a,b] . Функция f(x) непрерывна на интервале [a,b] и на концах отрезка принимает значения разных знаков, т.е. f(a) f(b)<0 . Тогда на интервале содержится по крайней мере один корень уравнения f(x)=0. Если функция f(x) имеет непрерывные производные, первая производная сохраняет свой знак на интервале [a,b], то корень уравнения f(x)=0 единственный. Найти приближенное значение корня уравнения f(x)=0, вычисленное с точностью ε, ε-малое положительное число.
Решение поставленной задачи состоит из двух этапов:
1. отделение корней (определение интервалов, где находятся корни);
2. уточнение изолированного корня до заданной точности ε.
На первом этапе применяют графический метод и метод деления отрезка пополам. На втором этапе используют метод деления отрезка пополам, метод касательных, метод хорд, комбинированный метод итераций.
|
|
|
Метод касательных (Ньютона) и его модификации.
Пусть ξ – корень уравнения f(x)=0 отделен на отрезке [a,b], причем 
непрерывные и сохраняют определенные знаки при а< x< b. Найти приближенное значение корня.
Выберем в качестве начального приближения х0=а и проведем в точке А0(а, f(a)) касательную к графику функции f(x). Абсцисса пересечения касательной с осью Ох является первым приближением к корню.
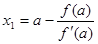или х0=а 
Через точку А1(х1, f(х1)) снова проведем касательную, абсцисса точки пересечения которой даст второе приближение х2 корня ξ и т.д. Очевидно, что уравнение касательной в точке Аn(хn, f(хn))
и алгоритм метода Ньютона запишется как:
.
В качестве исходной точки выбирается тот конец интервала [a,b], которому отвечает ордината того же знака, что и знак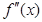 
: 
.
Метод Рыбакова
Эта модификация метода Ньютона может быть использована при поиске всех корней уравнения f(x)=0 на отрезке [a,b]. Пусть задано некоторое число М такое, что 
, z 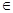[a,b], следовательно , 
.
Тогда алгоритм Ньютона запишется как:
, х0=а,
если xn+1>b, то все корни найдены;
если 
, то xn+1 – один из корней уравнения. Начальное приближение следующего корня х0=xn+1 +2ε и т.д.
|
|
|
Функция на заданном отрезке может иметь производную с разрывами первого рода. Число приближений определяется : 
.
Дата добавления: 2021-12-10; просмотров: 210; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!