Метод парабол (метод Симпсона)

Решение обыкновенных дифференциальных уравнений и систем

Дифференциальные уравнения являются основным математическим инструментом моделирования и анализа разнообразных явлений и процессов в науке и технике.

Методы их решения подразделяются на два класса:

ü аналитические методы, в которых решение получается в виде аналитических функций;

ü численные (приближенные) методы, где искомые интегральные кривые получают в виде таблиц их численных значений.

Применение аналитических методов позволяет исследовать полученные решения методами математического анализа и сделать соответствующие выводы о свойствах моделируемого явления или процесса. К сожалению, с помощью таких методов можно решать достаточно ограниченный круг реальных задач. Численные методы позволяют получить с определенной точностью приближенное решение практически любой задачи.

Решить дифференциальное уравнение

(1)

численным методом означает, что для заданной последовательности аргументов 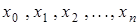и числа 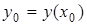, не определяя аналитического вида функции , найти значения , удовлетворяющие условиям:

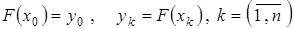Метод Эйлера

Этот метод является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других численных методов.

Пусть дано дифференциальное уравнение с начальными условиями (задача Коши)

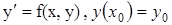(2)

и удовлетворяются условия существования и единственности решения.

Требуется найти решение задачи Коши (2) на отрезке . Находим решение в виде таблицы . Для этого разобьем отрезок на равных частей и построим последовательность где - шаг интегрирования. Проинтегрируем исходное уравнение на отрезке :

Полученное соотношение можно переписать так

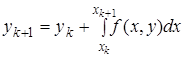(3)

Если считать подинтегральную функцию постоянной на участке и равной значению в начальной точке этого интервала 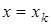, то получим

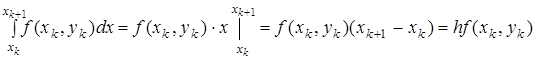
Подставляя полученный результат в формулу (3) получаем основную расчетную формулу метода Эйлера:

(4)

Вычисление значений 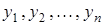осуществляется с использованием формулы (19) следующим образом. По заданным начальным условиям 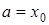и полагая в выражении (4) вычисляется значение

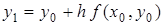(5)

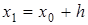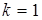Далее определяя значение аргумента по формуле , используя найденное значение и полагая в формуле (4) вычисляем следующее приближенное значение интегральной кривой 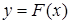, как

(6)

Поступая аналогичным образом при 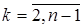определяем все остальные значения , в том числе последнее значение , которое соответствует значению аргумента .

Таким образом, соединяя на координатной плоскости точки отрезками прямых в качестве приближенного представления искомой интегральной кривой 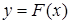, получаем ломанную линию с вершинами в точках .

Метод Эйлера может быть применен к решению систем дифференциальных уравнений.

Пусть задана система двух уравнений первого порядка

(7)

с начальными условиями

Необходимо найти решение этой задачи Коши. Проводя аналогичные рассуждения, получаем расчетные формулы вида:

(8)

где - шаг интегрирования.

При расчетах полагается, что 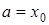и 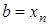. В результате применения расчетной схемы (8) получается приближенное представление интегральных кривых 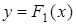и в форме двух ломанных Эйлера, построенных по полученным таблицам . Точность метода Эйлера .

Программа решения рассмотренного уравнения методом Эйлера может иметь следующий вид:

program ОDU; {Решение ОДУ методом Эйлера}

var

i,n: integer ;

x,у,h: real;

function f(a,b:real):real;

begin

f:=(вводим функцию);

end;

begin

writeln ('Введете начальные значения x и у') ;

readln(x,y) ;

writeln {'Введите шаг');

readln(h);

writeln ('Введите число шагов');

readln(n) ;

writeln (' РЕШЕНИЕ’);

writeln (' х у1);

writeln (х:8:3,у:8:3);

for i:=l to ndo

begin

у: =y+h*f (x, y) ;

x:=x+h;

writeln (x:8:3,у:8:3);

end;

end.

Решение задачи №1

Формулировка: найти численное решение задачи Коши на отрезке [x₀, x₀+1] методом Эйлера с шагом h=0,1. Найти точное решение и оценить погрешность двумя способами: 1)сравнить с точным решением; 2) с помощью двойного просчета.

Уравнение второго порядка сводится к системе уравнений первого

порядка путём введения новых переменных: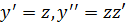

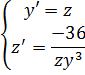
z(0)=2

1 шаг: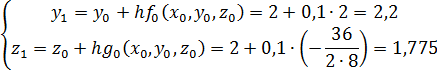

2 шаг:

Результаты оформим в таблицу.

Так как у нас от х не зависят ни f, ни g, то от отрезка результат не зависит.

i	x	y	z
0	0	2	2
1	0,1	2,2	1,775
2	0,2	2,3775	1,584526
3	0,3	2,535953	1,415466
4	0,4	2,677499	1,259518
5	0,5	2,803451	1,110612
6	0,6	2,914512	0,963496
7	0,7	3,010862	0,812573
8	0,8	3,092119	0,650254
9	0,9	3,157144	0,462992
10	1	3,203444	0,215908

Найдем точное решение.

Понижаем порядок уравнения.

Решаем это уравнение.

Уравнение с разделяющимися переменными.

Возвращаемся к исходным обозначениям.

Y(0)=3

Y’(0)=2

С=0

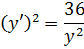
Сделаем замену

И т.д.

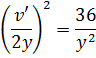
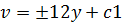
Так как задача Коши, то c1=-27

Методы численного интегрирования.

Вычислить определенный интеграл , где – непрерывная функция x в интервале , можно с помощью аналитической формулы, если использовать прием формального интегрирования по формуле Ньютона-Лейбница (I.)

, (I.)

где – первообразная функция для заданной функции .

Однако во многих случаях не удается найти никакой аналитической формулы в виду невозможности определения .

В таких случаях приходится применять методы численного интегрирования.

Основной принцип построения всех приближенных формул численного интегрирования состоит в том, что интервал интегрирования разбивается на множество меньших отрезков, внутри которых подынтегральная кривая заменяется с некоторой степенью точности более простыми функциями, интегралы от которых можно вычислить, используя ординаты на концах отрезков.

Метод прямоугольников

Вычисление интеграла равносильно вычислению площади некоторой фигуры – криволинейной трапеции с параллельными «основаниями» x = a, x = b и «боковыми сторонами» y =0, y = f ( x ), рис. I.

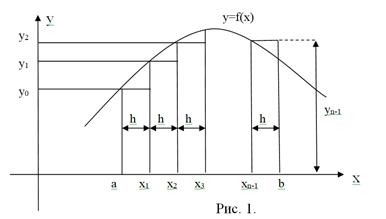
Разобьем интервал интегрирования на n равных частей, каждая длиной h =( b - a )/ n.

Приближенное значение интеграла получается в виде сумм площадей n прямоугольников, высота которых равна значению f ( x ) на левом краю каждого подинтервала, т.е. формула численного интегрирования имеет вид (2.):

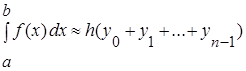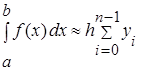или (2.)

и называется формулой «левых» прямоугольников.

Если в качестве приближенного значения площади для каждого подинтервала принять площадь прямоугольника, высота которого равна значению f ( x ) на правом краю подинтервала, то формула численного интегрирования будет иметь вид 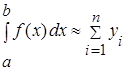(3.):

(3.)

и называется формулой «правых» прямоугольников.

Метод трапеций

В соответствии с полученными ранее формулами «левых» и «правых» прямоугольников истинное значение интеграла лежит между приближенными значениями, определяемыми по этим формулам (рис. 2), т.е. лучшую формулу численного интегрирования можно получить, взяв среднее арифметическое этих значений:

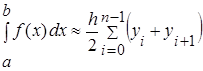. (4)

Эта формула (4) описывает метод трапеций для численного интегрирования, т.е. приближенное значение интеграла получается в виде суммы площадей «n» трапеций.

Следовательно, формула трапеций для численного интегрирования имеет вид:

Остаточный член имеет вид

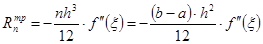, a<ξ<b.

На практике для оценки абсолютной погрешности формулы трапеций применяют следующие соотношения:

При этом, как правило, получаем для завышенную оценку.

2. Правило Рунге (n-четное) дает более точную оценку :

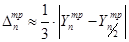Но при этом может получиться для заниженная оценка, чего следует опасаться.

Метод парабол (метод Симпсона)

Это наиболее широко известный и применяемый метод численного интегрирования.

Метод аналогичен рассмотренным ранее методам прямоугольников и трапеций: интервал интегрирования разбивается на множество более мелких отрезков; однако для вычисления площади под каждым из отрезков через три последовательных ординаты разбиения проводится квадратичная парабола (рис. 3).

Формулу Симпсона выведем проводя параболу через три ординаты на концах двух соседних интервалов и складывая получившиеся при этом площади.

Действительно, определяя y ₀ , y ₁ , y ₂:

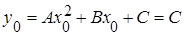
имеем ,

т.е. (5)

окончательно

или

(6)

Последняя формула (6) называется формулой Симпсона.

Поскольку в методе Симпсона парабола проводится через три ординаты на концах двух соседних интервалов, то при реализации этого метода необходимо требовать, чтобы «n» было четным числом.

Дата добавления: 2021-12-10; просмотров: 131; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 Следующая ⇒

Мы поможем в написании ваших работ!