Расстояние от точки до плоскости.
Расстояние от точки 
до плоскости 
вычисляется по формуле:
.
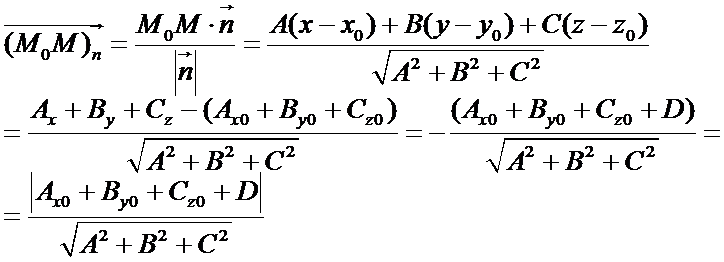
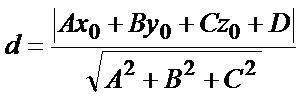Общее уравнение прямой в пространстве. Векторное, каноническое и параметрическое уравнения прямой в пространстве.
Прямая в пространстве рассматривается как линия пересечения двух плоскостей и поэтому может быть задана системой уравнений:
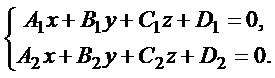
Эта система уравнений называется общим уравнением прямой в пространстве.
Пусть прямая проходит через точку М0 :
Векторное уравнение прямой.
Параметрические уравнения прямой в пространстве (когда координаты точек прямой задаются как функции одной и той же переменной t, называемой параметром точки) имеют вид:
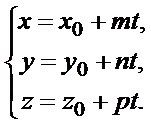
Здесь 
, 
, 
− координаты фиксированной точки 
, через которую проходит прямая, 
, 
, 
− координаты направляющего вектора 
(любого вектора, параллельного прямой).
Каноническое уравнение прямойв пространстве
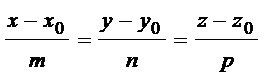
это символическое уравнение, получаемое из параметрического исключением параметра t.
Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
Вопросы взаимного расположения плоскости 
и прямой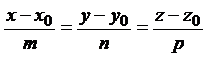 
сводятся, в основном, к установлению взаимного расположения нормального вектора плоскости 
и направляющего вектора прямой 
.
Углом между прямой и плоскостью называется наименьший угол между прямой и ее проекцией на плоскость:
.
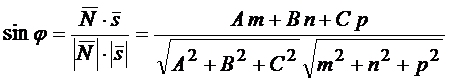Условие параллельности прямой и плоскости определяется условием перпендикулярности векторов 
и 
:
|
|
|
.
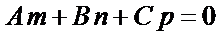Условие перпендикулярности прямой и плоскости определяется условием параллельности векторов 
и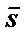 
:
.
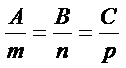Определение точки пересечения прямой и плоскости
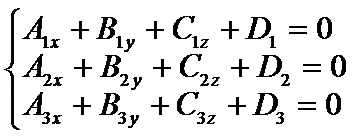
Для нахождения точки пересечения решаем систему из трех уравнений. Если решение единственное, то оно является корд. Точки пересечения. Если решений бесконечное мно-во, то прямая принадлежит плоскости. Если решений нет, то прямая не пересекается с плоскостью.
Скрещевающиесь прямые
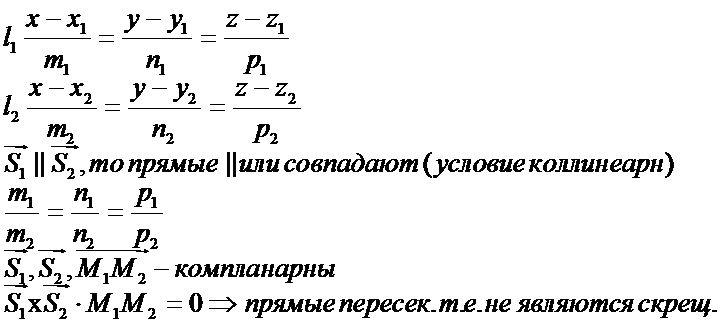
Уравнение прямой проходящей через две данные точки. Уравнение прямой в отрезках.
В системе Oxy общее уравнение прямой − это уравнение вида 
. Частные случаи:
1) 
, т. е. 
, 
, 
− прямая проходит через начало координат;
2) 
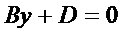, т.е. 
, 
, 
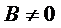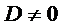− это уравнение преобразуется к виду 
, оно определяет прямую параллельную оси Оx; аналогично, уравнение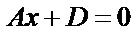 
или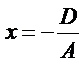 
определяет прямую параллельную оси Оy;
3) 
− прямая совпадает с осью Оx; аналогично, 
− это уравнение прямой, совпадающей с осью Оy.
Если в общем уравнении прямой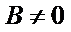 
, то разделив его на 
, получим уравнение вида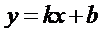 
, которое называется уравнением прямой с угловым коэффициентом. В нем 
.
Коэффициент k называется угловым коэффициентом, так как он равен тангенсу угла наклона прямой к оси Оx ( 
). Свободный член уравнения b равен ординате точки пересечения прямой с осью Оy и называется величиной смещения прямой вдоль оси Оy.
|
|
|
Прямая на плоскости может быть задана каноническим 
или параметрическими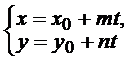 
уравнениями.
Здесь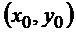 
− координаты точки, через которую проходит прямая, 
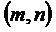− координаты направляющего вектора прямой.
Уравнение прямой, имеющей угловой коэффициент k и проходящей через точку 
, имеет вид 
.
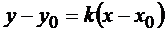Уравнение прямой, проходящей через две заданные точки 
и 
, имеет вид 
.
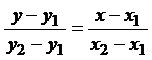Уравнение прямой в отрезках 
, где a и b − это величины отрезков, отсекаемых прямой от координатных осей, т. е. прямая проходит через точки 
и 
.
Дата добавления: 2018-02-18; просмотров: 700; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!