Метод направленного перебора.
Данный метод аналогичен методу равномерного поиска для функции одной переменной.
Делим области допустимых значений 
и 
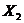на равные отрезки таким образом, чтобы количество отрезков по обеим осям было равно 
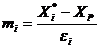, где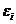 
- величина допустимой погрешности. 
. Проведя перпендикуляры к осям во всех выделенных точках, получаем сетку на плоскости X1, X2 с количеством узлов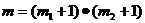 
(рис. 3.4). Вычисляем значения 
во всех узлах (рис. 3.4.). Сравниваем полученные значения и за решение принимаем координаты узла с наибольшим значением целевой функции .
Рис. 3.4.
Чем меньше шаг сетки, тем точнее результат, но и выше трудоемкость. На практике данный метод применяется только для вычисления глобального максимума невыпуклых функций.
Все остальные применяемые на практике методы, представляют собой итерационные многошаговые процедуры, в которых на каждом шаге расчета должно получаться большее значение целевой функции, чем на предыдущем.
Каждый метод включает в себя:
1) правило перехода от одного шага к другому,
2) правило остановки расчета.
В зависимости от правила перехода численные методы делятся на:
1. методы нулевого порядка, в которых правило перехода требует вычисления только самой целевой функции,
2. методы первого порядка (градиентные методы) в которых требуется вычисление первых частных производных целевой функции,
3. методы второго порядка – требуют вычисления вторых частных производных целевой функции.
|
|
|
Ниже будут рассмотрены только методы нулевого и первого порядков, т.к. в задачах оптимизации с возможными неточностями в исходных данных и с функциями, заданными алгоритмически, характерными для оптимизации технологических процессов, вычисление матрицы вторых производных приводит к значительным ошибкам и методы второго порядка не находят применения.
Методы нулевого порядка.
Метод Гауса-Зайделя (покоординатного поиска).
1). Для некоторого начального значения X(0) = (X1(0), X2(0)… Xn(0)) фиксируют все координаты вектора X кроме одной (для определённости X1) и производится поиск максимума функции одной переменной с помощью одного из методов, рассмотренных в разделе 2.
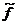0 (X1) = ¦0 (X1, X2(0),…, Xn(0)) →max.
Очевидно, что в процессе такой оптимизации будет меняться только одна переменная X1 , в результате получаем точку
X01 = ( X10(1), X2(0), Xn(0) ), где X10(1) = arg max 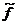0 (X1)
 |
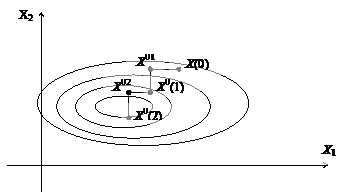Рис. 3.5
2). Фиксируя в точке X01 все координаты X кроме второй, повторяют поиск максимума функции по X2. И, так до последней составляющей Xn. Цикл алгоритма завершается после n кратной операции одномерной оптимизации вдоль каждой из координат, после чего его повторяют, получая точки Xi0(2), в каждой из которых значение ¦0 не меньше предыдущего.
|
|
|
На рис. 3.5. представлена геометрическая интерпретация метода Гауса-Зайделя для случая функции двух переменных f (X) = f (X1, X2).
Расчёт заканчивается, когда |DXi(N)| <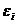 
, или D¦0 (N)< e, где 
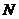– номер цикла поиска.
DXi(N)= Xi(N)- Xi(N-1);
Df0(N)= f0(N)- f0(N-1);
Пример: Выполнить первый цикл поиска максимума функции:
¦0(X1, X2) = - X12 - X1X2 – X22 - 3X2 ® max, X1(0) = X2(0) = -1,
т.е. X(0)=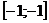 
.
Фиксируем X2= -1 и, подставляя это значение в целевую функцию, получаем
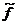0(X1) = - X12 + X1 – 1 + 3 = -X12 + X1 + 2 ®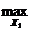 
Используем необходимые условия max функции одной переменной
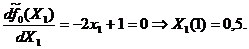
Получаем точку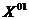 
=[0,5; -1].
Фиксируем 
=0,5 и, подставляя это значение в целевую функцию, получаем:
.
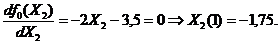
После первого цикла поиска получаем точку:
(1)=[0,5; -1,75],
Проверим, увеличилось ли в результате значение целевой функции
f0[ 
(1)]=-0,25+0,5*1,75-(-1,75)2+3*1,75≈2,8 > f0 [X(0)] = 0,
значит первый цикл вычислений сделан правильно.
В случае так называемых овражных функций (рис. 3.6), возможна остановка алгоритма в точках, далеких от действительного максимума, т.к. направления поиска в данном методе жёстко фиксированы вдоль осей координат и совершенно не учитывают характер функции ¦0( 
).
|
|
|
 |
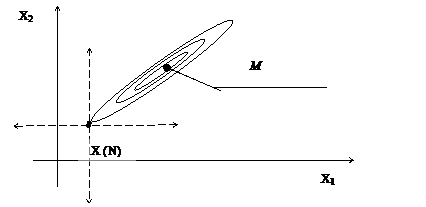Рис. 3. 6
Допустим, что после N-го цикла поиска мы попали в точку X(N) (см. рис. 3.6.). Любое из дальнейших возможных направлений поиска, указанных на рис. стрелками, очевидно приведет к уменьшению значения целевой функции. Таким образом, точка X(N) будет признана max исследуемой целевой функции, хотя на самом деле max находится в точке М.
Симплекс-метод
При использовании этого метода направление очередного шага поиска определяется в зависимости от значения целевой функции в вершинах выпуклого многогранника, называемого симплекс. При n-переменных симплекс имеет (n+1) вершину. В двумерном пространстве (n=2) симплексом является треугольник. Симплекс называется регулярным, если размеры всех его граней одинаковы.
Из любого симплекса, отобразив одну из его вершин симметрично, относительно противоположной грани, можно получить новый симплекс.
Алгоритм поиска максимума состоит в следующем:
|
|
|
1. Строится исходный симплекс S0, который включает в себя в качестве одной из вершин исходную точку 
. По заданной длине грани определяют координаты остальных вершин и значения функции ¦0 во всех вершинах.
2. Следующий симплекс S1 строится зеркальным отображением вершины с минимальным значением целевой функции относительно противоположной грани.
3. Определяют значения ¦0 в вершинах симплекса S1, строят симплекс S2 и т.д.
Доказано, что при этом центр симплекса движется в сторону точки максимума целевой функции, вблизи от которой происходит зацикливание. Наличие зацикливания – признак приближения к максимуму и может быть использовано как условие для завершения вычислительной процедуры. Скорость поиска и точность зависят от размера грани, чем она больше, тем скорость выше, а точность меньше. Поэтому на практике используют модификации симплексного метода, в которых размер грани уменьшается, по мере приближения к точке максимума. Условием окончания поиска может служить уменьшение грани симплекса до заданной величины e.
Вычисление координат отражённой вершины каждого следующего симплекса осуществляется по формуле:
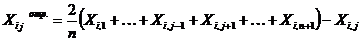(3.7),
где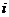 
- i-тая координата 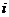=1,2… 
, отражённой j-той вершины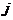 
= 1, 2, …, ( +1).
Пример:
Определить max функции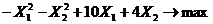 
Принять начальную точку с координатами 
= 2, 
= 0 и 
– длина грани. Задача двумерна, следовательно, симплексом является треугольник.
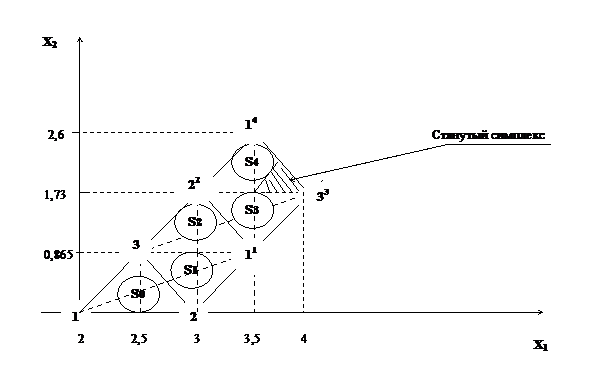
Рис. 3.7
Последовательность решения задачи геометрически представлена на
рис. 3.7. Результаты расчетов сведены в таблицу.
Таблица
| № верш. | X1 | X2 | ¦0 |
| 1 | 2 | 0 | 16 |
| 2 | 3 | 0 | 21 |
| 3 | 2.5 | 0.865 | 21.5 |
| 11 | 3.5 | 0.865 | 25.5 |
| 22 | 3 | 1.73 | 27 |
| 33 | 4 | 1.73 | 28 |
| 14 | 3.5 | 2.6 | 26.4 |
Строим симплекс S0, определяем координаты его вершин 1, 2, 3, рассчитываем значения целевой функции f0 в вершинах и заносим результаты в таблицу. Наименьшее значение f0=16 получается для вершины 1, поэтому отображаем эту вершину симметрично, относительно противоположной грани, рассчитываем координаты отображенной вершины 11 в соответствии с выражением (3.7) и строим симплекс S1. При расчетах координат отображенных вершин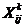 
будем пользоваться следующими обозначениями:
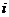- номер координаты;
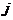- номер вершины;
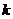- номер отображения;
то есть 
- это вторая координата первой вершины после первого отображения и т.д., причем отображения нумеруются подряд, независимо от того, какая вершина отображается.
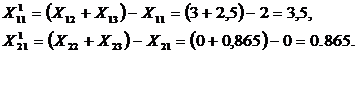
Вершинами S1 являются точки 2, 3,11. Так как значения f 0 в вершинах 2 и 3 уже известны, рассчитываем только значение целевой функции в вершине 11. Результаты расчетов заносим в таблицу. Сравнивая значения f 0 в вершинах симплекса S1, получаем наименьшее значение f 0 = 21 для вершины 2, поэтому отображаем эту вершину, аналогично предыдущей, рассчитываем координаты отображенной вершины 22 и строим симплекс S2, вершинами которого являются точки 3, 11, 22.
 |
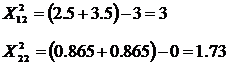Проведя аналогичные операции с симплексом S2, получаем симплекс S3 с вершинами 11, 22, 33, а затем и симплекс S4 с вершинами 22, 33, 14.
Для симплекса S4 минимальным является значение целевой функции в вершине 14 (см. таблицу). Поэтому для построения следующего симплекса S5 необходимо отобразить вершину 14 и таким образом S5 будет совпадать с S3, т.е имеет место зацикливание. Для повышения точности расчёта целесообразно уменьшить грань симплекса, стянув его к вершине с большим значением целевой функции f0 (вершина 33 ), например путем деления первоначальной длины грани пополам (см. рис. 3.7).
После чего процедура поиска продолжается. Расчёт заканчивается, когда зацикливается симплекс с размером грани меньше заданного e, и за решение задачи принимаются координаты вершины последнего симплекса, с максимальным значением целевой функции.
Дата добавления: 2018-02-15; просмотров: 1769; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!