Интерполирование на неравномерной сетке
Выше мы утверждали, что погрешность интерполяционного многочлена Лагранжа определяется величиной
Rn(f)= 
.
Если максимум n+1-й производной нам неподвластен, то произведение значений (x-xi) в ряде случаев (мы знаем функцию и желаем заменить ее более простой) существенно зависит от выбора узлов интерполирования.
П.Л.Чебышев доказал, что для tÎ[-1,1] минимум Q(t)= 
достигается при выборе узлов –1£ x0<x1<...<xn£ 1 так, чтобы Q(t)=Tn+1(t)/2n. Соответственно, максимум | Q(t) |=2-n.
Соответственно, интерполяционный многочлен n-й степени с узлами интерполяции
(4
обеспечивает по точности лучшую интерполяцию, чем интерполяция на равномерной сетке.
Есть еще и другие соображения, связанные с использованием узлов Чебышева.
Казалось бы, с ростом числа узлов максимум Rn(f)®0 и значения многочленов Лагранжа все ближе к “истинным” значениям функции, однако производные для многих функций не являются ограниченными и последовательность Rn(f) расходится - феномен Рунге [17]. Например, построив многочлен Лагранжа для функции f(x)=1 /(1+10x2) при равномерном выборе n=11 узлов в интервале [-1,1] , обнаруживаем близ концов интервала семикратное отклонение его значений от истинных (рис.6). При выборе того же количества узлов по Чебышеву осцилляция значений полинома сохраняется, но в пределах разумного.
Интерполирование функций двух переменных.
Пусть задана таблица значений функции двух переменных z=f(x,y) и требуется найти z=f(x*,y*) .
|
|
|
Эта задача решается в два этапа: сначала для всех табличныx значений yk проводится интерполяция по x для указанного x* и затем по найденной табличке значений f(x*,yk) проводится интерполяция по y для заданного y*.
Численное дифференцирование.
Задача численного дифференцирования возникает в случае, когда функция задана таблично или сложным аналитическим выражением.
Большинство формул численного дифференцирования получается дифференцированием интерполяционных формул.
Так, получив интерполяционный многочлен Лагранжа, обычным дифференцированием можно получить его производные любого порядка (не следует только забывать о возможном возрастании погрешности).
Дифференцированием формулы Ньютона интерполирования вперед с последующим заданием t=0 можно получить оценки
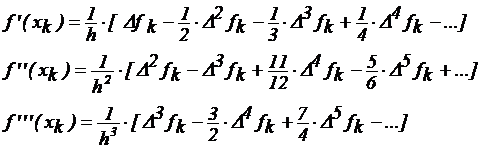( 1 )
На практике редко учитывают разности высоких порядков и используют небольшое число слагаемых. Если найти первые члены разложения функции в ряд Тейлора, то можно получить простые и эффективные в приложениях оценки:
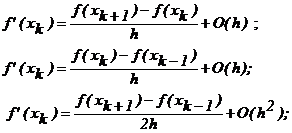( 2 )
( 3 )
Множество подобных и более точных формул численной оценки производных для табличных функций (случай равноотстоящих узлов) приведено в [3] . Этими оценками можно пользоваться при дифференцировании как в середине, так и на концах таблицы.
|
|
|
Для построения формул численного дифференцирования можно использовать и метод неопределенных коэффициентов.
Обозначим для краткости f(xk)=fk . Пусть
f’(xk)=A0 f0+A1 f1+...+Am fm ( 4 )
Полагая, что эта формула точна для полинома m-й степени и, в частности, для полиномов
1 , x- xk , (x- xk)2, . . . , (x- xk)m, ( 5 )
подстановкой этих полиномов в указанную формулу получаем систему m+1 уравнений для определения неопределенных коэффициентов.
Интерполирование сплайнами.
при Поэтому для уменьшения погрешности иногда предпочитают область интерполяции разбить на несколько подынтервалов и на каждом из них использовать для аппроксимации полином невысокой степени, т.е. прибегают к кусочно-полиномиальной аппроксимации.
Один из способов такой аппроксимации базируется на т.н. интерполяции сплайнами [2,9] .
Пусть интервал [a,b] разбит на N подынтервалов с граничными узлами a=x0 < x1 < ... < xN-1 < xN=b .
|
|
|
Сплайном m-го порядка для f(x) на [ a,b ] называют кусочную функцию P(x) = { P1(x),P2(x),...,PN(x) }, удовлетворяющую условиям:
1) все функции Pk(x) (k=1,2,...,N) - полиномы m-го порядка;
2) на концах подынтервалов соблюдаются условия интерполяции и непрерывности
P1(x0)=f(x0),
P(xk)=Pk+1(xk)=f(xk) , k=1,2,...,N-1 , (48)
PN(xN)=f(xN);
3) на концах подынтервалов соблюдаются условия непрерывности производных до m-1-го порядка
Pk(s)(xk) = Pk+1(s)(xk) , k=1,2,...,N-1 , s=1,...,m-1. (49)
Если взять простейшую задачу - аппроксимацию линейными сплайнами (m=1)
Pk(x)=Ak×x+Bk , k=1,2,...,N , (50)
то из (48) возникает система 2N уравнений c 2N неизвестными
A1× x0 + B1= f(x0),
Ak× xk + Bk = f(xk), k=1,2,...,N, (51)
Ak+1×xk+B k+1=f(xk), k=1,2,...,N-1,
решение которой тривиально
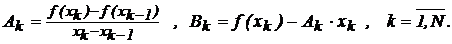(52)
При аппроксимации квадратичными сплайнами
Pk(x)=Ak×(x-xk-1)2+Bk(x- xk-1) +Ck , k=1,2,...,N , (53)
возникает система 3N-1 уравнений с 3N неизвестными
×Ck= f(xk-1), k=1,2,...,N,
Ak×(xk-x k-1)2+Bk(xk-x k-1) +Ck= f(xk), k=1,2,...,N,
|
|
|
2Ak×(xk-x k-1)+Bk= Bk+1 , k=1,2,...,N-1.
Недостающее уравнение получают, ставя какое-нибудь условие на одном из концов интервала, например, требуя обращения в нуль первой производной при x= x0 , откуда B1= f¢(x0) =0 . Можно и прибегнуть к более точной оценке производной : например, если x1=x0+h и x2=x0+2h, то можно принять (см. методы численного дифференцирования) f¢(x0)=[-3f(x0)+4f(x1)-f(x2)]/2h или аналогичные аппроксимации.
Таким образом,
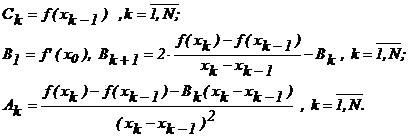(48)
Аналогично можно получить параметры кубической сплайн-интерполяции [15]. Сплайны более высокого порядка практически никто не использует. Достоинством сплайнов степени выше первой является возможность простой и достаточно хорошей оценки не только функции, но и ее производных. Интерполяция сплайнами может облегчить и процесс численного интегрирования.
7. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ.
Если для функции f(x), определенной на [a,b], удается найти первообразную F(x) (“взять интеграл”), то значение интеграла от этой функции с легкостью определяется по формуле Ньютона
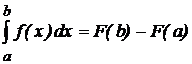. ( 6 )
Для большинства функций поиск первообразной нереален, не говоря уж о табличных функциях, и потому возникает задача численной оценки интеграла с какой-то точностью.
Дата добавления: 2018-02-18; просмотров: 1488; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!