Метод простой итерации и сходимость итераций.

⇐ ПредыдущаяСтр 5 из 13Следующая ⇒

При больших значениях n прямые методы лишь формально являются точными, в реальности давая весьма высокую вычислительную погрешность.

Идея методов итераций (последовательных приближений) состоит в преобразовании системы уравнений AX=B к системе

Тот же принцем, в простой итерации. Мы берем какую-то начальную точку приближения и от нее двигаемся в цикле все ближе к значению с нужной нам точностью.

Сначала нам понятное дело надо заменить уравнения в системе и привести их к виду X = a X + b ну короче выразить из каждого уравнения по иксу. Чтобы ваш цикл не расколбасило, нужно соблюсти условие ||a||<1, т.е. норма матрицы должна быть меньше 1. Чтобы так было, когда будите выражать иксы из уравнений, нужно в каждом уравнении найти наибольший коэффициент и выражать тот икс, который при этом максимальном коэффициенте.

Метод Зейделя.

Перепишем процесс простой итерации (17) в развернутом виде

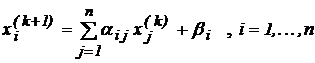. ( 17a)

Метод Зейделя отличается тем, что на очередной итерации берут не оценки предыдущей итерации, а самые последние из полученных:

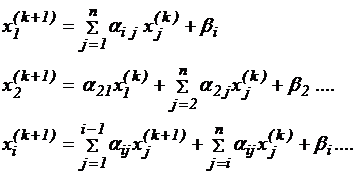( 19)

Как правило, использование метода Зейделя дает ускорение сходимости приближений к истинному решению. Условия сходимости те же, что и для метода простой итерации.

Очевидно, что при решении систем небольшой размерности использование итерационных методов едва ли разумно; при большой размерности они дают достаточно точное решение при любом начальном приближении, т.е. устойчивы к возникновению вычислительных ошибок, чем не могут похвастаться прямые методы.

Метод прогонки для систем с трехдиагональной матрицей.

Этот метод для трехдиагональных матриц, это когда заполнена главная диагональ и две по бокам, остальные элементы нули. Предполагают, что xk=Pk*Xk+1 + Qk, k+1 это коэффициент икса, k=0...n-1

Эту хреновину подставляют в уравнению вместо икса, делают преобразования с раскрытием скобок и прочее и в итоге получается ( a_k P_k-1 +b_k) x_k + c_kx_k+1 = d_k- a_k Q_k-1 , k=2, ... , n-1 , Потом через какую-то магическую щель вытаскивают формулы для нахождения этих коэффициентов P и Q, и для иксов. Метод состоит из двух ходов, сначала в прямом ходе нам нужно найти коэффициенты, а потом в обратном ходе сами иксы и все по формулам:

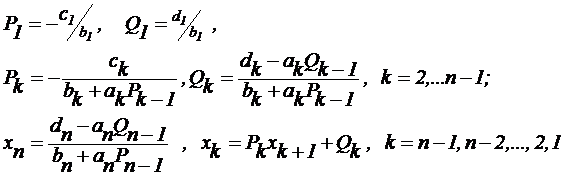
Краткая характеристика других методов.

За пределами нашего рассмотрения осталось достаточно много других методов решения линейных алгебраических систем.

Среди прямых методов рядом достоинств обладает метод отражений, который сводит исходную систему к системе с верхней треугольной матрицей при помощи т.н. ортогональных матриц отражения [6,23].

Можно среди прямых методов упомянуть метод окаймления [2] и метод ортогонализации [6], среди итерационных - метод сопряженных градиентов [6, 2] и метод подавления компонент [6].

Для решения систем высокого порядка используют клеточные методы, сводящие исходную задачу к последовательному перебору клеток матрицы коэффициентов и обращению матриц для этих клеток [6].

Особого рассмотрения заслуживают “плохо обусловленные” системы, где определитель матрицы близок к нулю. Здесь малейшее изменение исходных данных ведет к значительному изменению решения (решение неустойчиво по исходным данным). В принципе может обнаружиться и отсутствие решения - несовместность системы.

Разрешение такой ситуации, связанной обычно с некорректной постановкой задачи, предлагает метод регуляризации А.Н.Тихонова, сводящий исходную систему A× X = B к всегда совместной системе

( A^TA + a× E ) X = A^TB , a > 0 , ( 26 )

где A^T- транспонированная матрица, E - единичная матрица, параметр a выбирается с учетом требуемой точности решения и погрешности исходных данных [23].

Решение (26) дает для исходной системы т.н. нормальное решение (решение X системы A× X = B является нормальным, если его скалярные произведения со всеми линейно независимыми решениями обращаются в нуль). При поиске любого из решений вместо (26) берут систему

A^TA × X = A^TB , ( 27 )

решаемую методом квадратных корней или каким-то другим методом.

К решению (27) сводится и случай переопределенных систем, где число уравнений m превышает число переменных n. Решение таких систем иногда выполняют с учетом предпочтений. Здесь выбирают r уравнений и r неизвестных (r < n), полученную систему решают точно, а для системы оставшиеся m-r уравнений с n-r неизвестными решают методом наименьших квадратов (этот метод мы рассмотрим при изучении приемов аппроксимации; по существу он сводится к решению (27)).

5. ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ И МЕТОДЫ ЕЕ РЕШЕНИЯ.

Дата добавления: 2018-02-18; просмотров: 465; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!