Вариационное исчисление и методы оптимизации
1. Решить графическим способом
Решение:
Строим Х1ОХ2 и множество планов х, вектор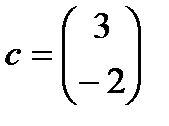 
и линию u=0 нулевого уровня (u^c)
zmax=z(4,8;1,4)=11,6
zmin : все точки отрезка BC (B(0;5), C(12/7;13/7))
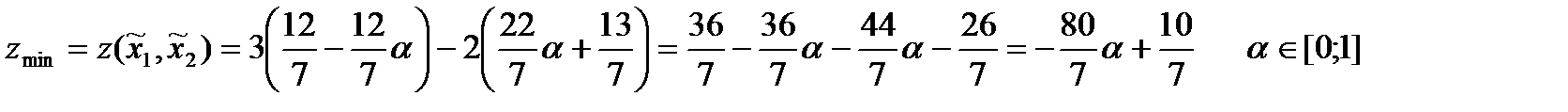
Ответ:zmax=11,6;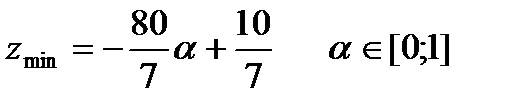 
Билет 13
Кольцо классов вычетов (опр-ние сравнимости двух целых чисел по натур-му модулю; св-ва сравнений; классы вычетов; операции на классах вычетов; кольцо классов вычетов).
Срав-ния в кольце целых чисел. Пусть mÎN, a и bÎZ, если m | (a-b) то пишут aºb (modm) и говорят, что а сравнимо с b по модулю m. Если m не делит (a-b), то a¹b (modm).
Т 9:Число aºb (modm) Û когда a и b имееют одинаковые остатки при делении на m.
Док-во:1)Пусть aºb (modm), b = qm + r, 0 £r<m. Т.к. aºb (modm), то тогда m | (a - b) Þ$ к ÎZ, a – b = кmÞa - (mq + r) = km, a = km + qm + r, a = (k + q)m + r, 0 £r<mÞa имеет остаток r
2)Пусть a и b имееют одинаковые остатки при делении на m, a = mq1 + r, b = mq2 + r, 0 £r<m
a – b = mq1 - mq2 = m(q1 - q2) Þ m | (a-b) Þ a º b (mod m).
Cв-ва сравнений не зависящие от модуля:
Лемма 9: Пусть mÎN, a и bÎZ, тогда справедливы следующие утверждения:
1) a º a (mod m), a Î Z.2) Если a º b (mod m), то b º a (mod m),3)Если a º b (mod m), b º c (mod m), то a º с (mod m).
Лемма 10:Ср-ния по одному модулю можно складывать, вычитать и умножать почленно.
Из леммы 9 и леммы 10 получаем следующие свойства:
1) к обеим частям можно прибавлять одно и тоже число.
2) обе части можно умножать на одно и тоже число.
3)слагаемые из одной части можно переносить в другую с противо-ным знаком.
|
|
|
4)к любой части сравнения можно прибавлять число кратное модулю.
5)Можно возводить в натуральную степень.
Cв-ва срав-ний зависящие от модуля:
Лемма 11:Обе части срав-ния и модуль можно умножить на одно и тоже натуральное число.
Док-во: aºb (modm) Þ (a - b) = mt, tÎNÞak - bk = mktÞmk | (ak - bk) Þakºbk (modmk)
Лемма 12: Если akºbk (modmk), c = НОД(m,k) Þaºb (modm/c)
Кольцо классов вычетов. Пусть mÎN, aÎZ, тогда a = mq + r, 0 £r<m, rÎ {0, 1, 2, …, m -1}. Обозначим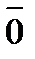 
-все целые числа, которые при делении на m дают остаток 0
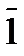-все целые числа, которые при делении на m дают остаток 1
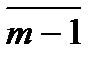-все целые числа, которые при делении на m дают остаток m-1, тогда
Множество всех классов вычетов по модулю m обозначается Zm
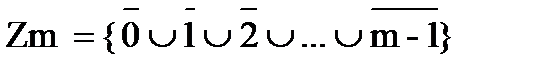где r – остаток при делении а на m
Т. 10: 
Множество Zmклассов вычетов по модулю m с введенными выше операциями ‘ + ’ и ‘ * ’ является полуаддитивным кольцом с единицей.
Лемма 13:Элемент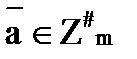 
обладает в Zm обратным элементом тогда и только тогда, когда числа а и m взаимно просты.
Т 11: Кольцо классов вычетов Zm является полем Û когда m – простое число
Лемма 14: Пусть mÎN, aÎZ. Если a и m взаимно просты и bºa (m), то b и m – взаимно просты.
Т 12(Эйлера): Если а и m взаимно просты, то аj(m)º 1 (m), где a1, a2,…, ak, k = j(m), НОД(ai,m) = 1.
|
|
|
Следствие (малая теорема Ферма): Если pÎP, a не делится на p, то аp -1º 1 (p)
Док – во: m = p, тогда аj(p)º 1 (p) Þ аp -1º 1 (p)
C помощью теоремы Эйлера в Zmможно находить обратный элемент. 
.
Следовательно,
13Методика введения понятия функции.
Общее понятие ф-ции вводится в 7 кл., хотя многие функциональные понятия вводятся в 9 кл. в теме «Числовые ф-ции». И лишь в 10 кл. учащиеся знакомятся с понятием «периодичности», а в 11 кл. с понятием «функция обратная к данной».
1) Понятие ф-ции вводится конкретно-индуктивным способом.
2) На основании конкретной формулы устанавливаются характеристические свойства общего понятия ф-ции: каждому аргументу функции сопоставляется единственное значение функции.
3) Формулируется определение ф-ции, сообщается учителем определение терминов «ОДЗ» и «ООФ».
4) Проиллюстрировать сказанное.
5) Привести контрпример понятия функции.
6) Рассмотреть упражнения .
7) Закрепить формулировку определения функции
По этой же схеме можно изучать и остальные общие функциональные свойства: чётность, монотонность, периодичность и т.д.
13 Найти матрицу, обратную матрице А
.
|
|
|
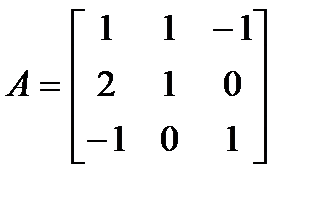Решение: Обратную матрицу можно искать только для квадратной матрицы, у которой определитель ≠ 0
т. к.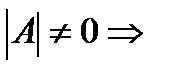 
обратная матрица существует
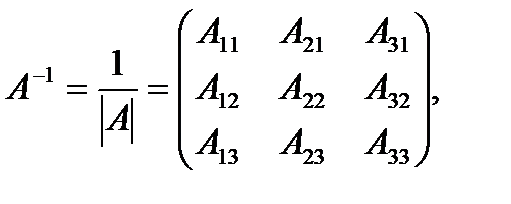Aij - алгебраические дополнения
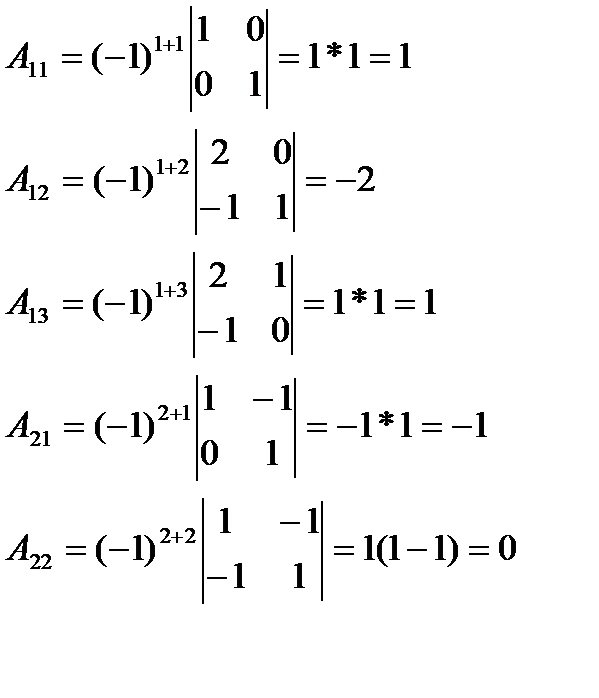
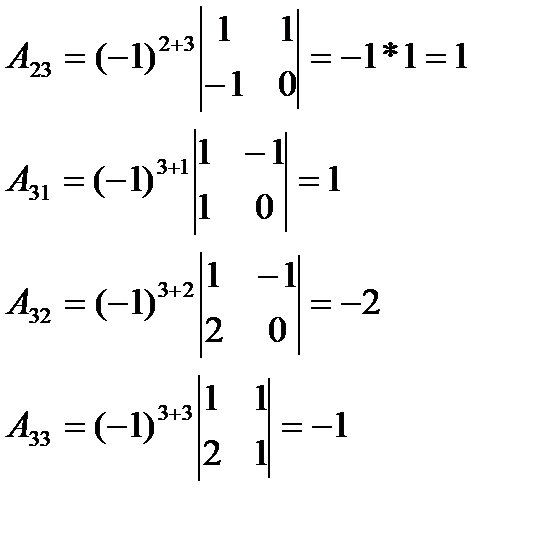
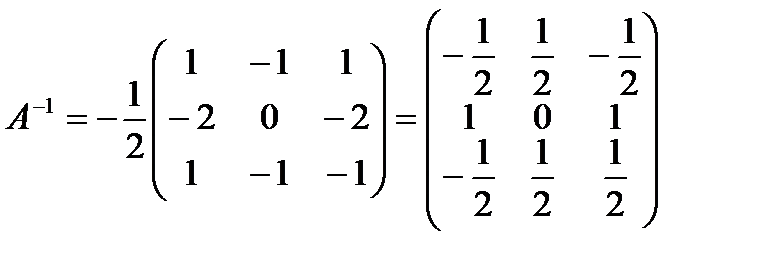Ответ: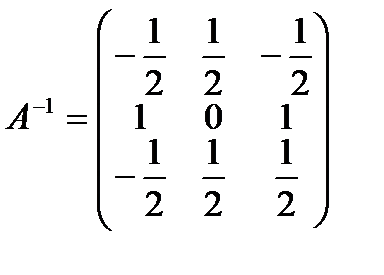 
Билет 14
Дата добавления: 2018-02-15; просмотров: 582; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!