ДУ-n, допускающие понижение порядка
10 y(n)=f(x)
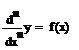
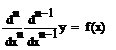 - ДУ-1 относительно y(n-1), с разделяющимися переменными
- ДУ-1 относительно y(n-1), с разделяющимися переменными
d(y(n-1))=f(x)dx
∫d(y(n-1))=∫f(x)dx+C
y(n-1)=∫f(x)dx+C
снова понижаем порядок
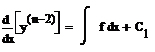 - ДУ-1 с разделяющимися переменными
- ДУ-1 с разделяющимися переменными
∫d(y(n-2))=∫(∫f(x)dx+C1)dx+C2
y(n-2)=∫(∫f(x)dx)dx+xC1+C2
 и т.д.
и т.д.
20 F(x, y(k), y(k+1),…, y(n))=0 (1)
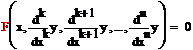
Нет явно 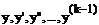 k=1,2,…,n
k=1,2,…,n
k=n случай 10 y(n)=f(x)
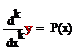 (2)
(2)
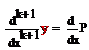 ,…,
,…, 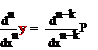 (3)
(3)
(2) и (3) в (1):
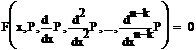 ДУ-(n-k) (4)
ДУ-(n-k) (4)
Замечание: вопрос о решении (4) остался открытым; хорошо, если оно сводится к известным ДУ.
30 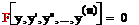 (5)
(5)
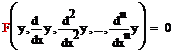
Нет явно «х»
Можно понизить порядок на единицу
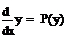 (6)
(6)
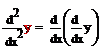 =
= 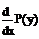 =
= 
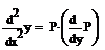 (7)
(7)
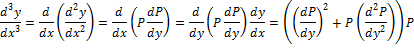
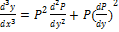 (8)
(8)
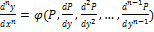 (9)
(9)
(6)-(9) в (5):
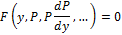
 (10)
(10)
Решение (10)
P=f(y,C1,C2,…,Cn-1) – общее решение (10)
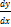 =f(y,C1,C2,…,Cn-1) – ДУ-1с разделяющимися переменными
=f(y,C1,C2,…,Cn-1) – ДУ-1с разделяющимися переменными
 - общий интеграл ДУ (5)
- общий интеграл ДУ (5)
Линейные ДУ высшего порядка(ДУ-n): однородные, неоднородные. Однородные ДУ-n: доказать теоремы о свойствах решений, понятие фундаментальной системы ЛОДУ-n. Доказать теорему о структуре общего решения ЛОДУ-n.
 (1)
(1)
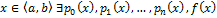

Если при всех рассматриваемых значениях x ф-я 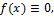 то уравнение (1) наз-ся линейным однородным, в противном сл-е он наз-ся лин-но неоднородным.
то уравнение (1) наз-ся линейным однородным, в противном сл-е он наз-ся лин-но неоднородным.
Введем оператор: 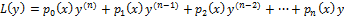 (2)
(2)
С помощью оператора (2) ур-е (1) примет вид: 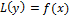
ЛОДУ-(n) Свойства решений 
Т1 Если 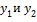 - решения, то
- решения, то 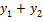 - тоже решения
- тоже решения
Д-во: 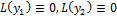
Тогда: 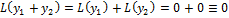
Т2 Если  - решение, то
- решение, то 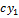 -тоже решение, где
-тоже решение, где 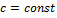
Д-во: 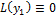 , тогда
, тогда
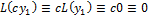
Понятие ФС ЛОДУ-(n)
Т 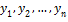 опред. на
опред. на 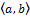 были лин-но незав-мы, необходимо и достаточно чтобы Вронскиан
были лин-но незав-мы, необходимо и достаточно чтобы Вронскиан 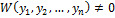 хотя бы в одной точке на
хотя бы в одной точке на 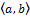
ТЕсли Вронскиан 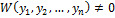 в точке
в точке 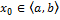 , то он не равен о ни в одной точке
, то он не равен о ни в одной точке 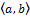
|
|
|
Оn - лин-но незав-х решений ЛОДУ-(n) наз-ся фундаментальной системой решений (ФСР)
Т о структуре общего решения ОЛДУ-(n)
Если 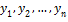 – ФСР ОЛДУ-(n)
– ФСР ОЛДУ-(n)
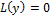 , то общ. Решение ОЛДУ-(n) имеет вид:
, то общ. Решение ОЛДУ-(n) имеет вид:
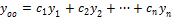 , (2)
, (2) 
Д-во: имеем 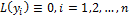
А) Тогда 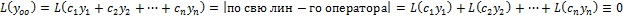
Б) Покажем, что задача Коши имеет единственное решение:
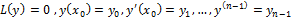 (3)
(3)
(2) в (3): 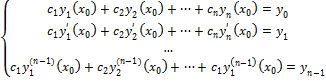 (4)
(4)
(4) – система лин-х неодн-х алгебр-х ур-й. Она имеет единственное решение, если опред-ль системы не равен 0.
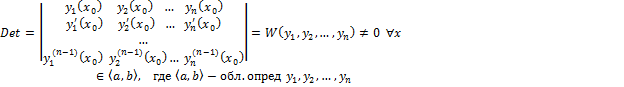
Значит (4) – единственное решение 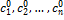
Подставляя найденное значение 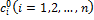 в (2) получаем решение задачи коши. Теор. Доказана
в (2) получаем решение задачи коши. Теор. Доказана
Вопрос.
П-ОЛДУ с постоянными коэффициентами
L(y)=yn+a1yn-1+…+an-1y’+any=0 (11)
a1,a2,…,an-const
Метод Эйлера: ищем решение в виде y=eλx λ-const (12)
y’=λeλx,y”=λ2eλx…yn=λneλx (13)
(12) и (13) в (11)
L(eλx)= λneλx+a1 λn-1eλx+…+an eλx
L(eλx)= (λn+a1 λn-1+a2 λn-2+…+an) eλx
L(eλx)=P(λ) eλx≡0 (14)
eλx≠0  xϵ(-∞;∞)
xϵ(-∞;∞)
Из (14) следует P( λ)≡λn+a1 λn-1+…an=0 (15)
Характеристическое уравнение(ху)
Задача. Интегрирование диф. уравнения свелось в
Случаи:
1. ХУ(15) имеет n различных вещественных корней
n решений λ1, λ2,.., λn y1= eλ1x,y2= eλ2x,…,yn= eλx(16)

 W(eλ1X,…, eλnX)= eλ1X eλ2X … eλnX
W(eλ1X,…, eλnX)= eλ1X eλ2X … eλnX
λ1 eλ1X x2 eλ2X… λn eλnX
………………………
|
|
|
λ1n-1 eλ1X … λnn-1 eλnX

 = eλ1X* eλ2X*… eλnX * I I …. I
= eλ1X* eλ2X*… eλnX * I I …. I
λ1 λ2 …. λn ≠0  xϵ(-∞;∞)
xϵ(-∞;∞)
λ1n-1 λ2n-1… λnn-1
определитель Вандер Монда т.е (16)-ФСР
Тогда yоо=с1y1+ с2y2+…+ сnyn= c1eλ1X + c2 eλ2X+…+ cn eλnX (17)
2. Среди корней XУ имеется комплексный корень λ1=α+iβ
Тогда имеется обязательно сопряжённый корень λ2=α+iβ
y1= eα+iβ)x=eαx(cosβx+isinβx)= eαxcosβx+ ieαxsinβx=u(x)+iv(x)=y1(c волнистой чертой) y2(c волн.ч)= eα-iβ=eαxcosβx-ieαxsinβx= u(x)+iv(x)
Теорема о комплексном решении ДУ
Пусть y=u+iv – комплексное решение ДУ. Тогда L(y)≡0 следовательно L(u)+iL(v)=0 следовательно 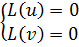
т.е u(x) и v(x)-действительное решение ДУ.
Вывод: двум комплексным сопряжённым корням λ1,2=α+iβ характеристического уравнения P(λ)=0 соответствует вещественное решение y1= eαxcosβx,y2= eαxsinβx
3. Среди корней ХУ корень λ1 кратности “к”
XУ P(λ)=(λ-λ1)kQn-k(λ)=0 (18)
 P’(λ)=k(λ- λ1)k-1 Q(λ)+ (λ- λ1)kQ’(λ)
P’(λ)=k(λ- λ1)k-1 Q(λ)+ (λ- λ1)kQ’(λ)
P’’(λ)= k(k-1)(λ-λ1)k-2Q(λ)+2k(λ-λ1)k-1Q’(λ)+ (λ-λ1)kQ’’(λ)
…………………………………………………………….. (19)
P(k) (λ)=k(k-1)…2*1Q(λ)+…+ (λ-λ1)kQk(λ)
Если λ1-корень ХУ(18), то (Q(λ1)≠0)
|
|
|
P(λ1)≡0 P’(λ1)=0,P’’(λ1)=0…,Pk-1(λ1),но Pk(λ1)=k’Q(λ1)≠0
Ранее имеем L(eλx)=P(λ) eλx=0 (20)
Продифференцируем соотношение (20) по λ:
(L(eλx))’λ=(P(λ) eλx)’λ ;(eλx)’=P’(λ) eλx+P(λ)x eλx
 L(x eλx)=P’(λ) eλx+P(λ)x eλx
L(x eλx)=P’(λ) eλx+P(λ)x eλx
Ещё раз дифференцируем по λ k-2 раз
L(x2 eλx)=P’’(λ) eλx+2P’(λ)x eλx+P(λ) eλxx2 (21)
Если в соотношении (21) подставим λ1-корень ХУ,то будем иметь
L(x eλx)=P’(λ1) eλ1x+P(λ1)x eλ1x=см 19=0 L(x eλ1x)≡0 следовательно x eλ1x тоже решение ОЛДУ-n. L(x2 eλ1x)=см 19=0+0+0=0 следовательно x2 eλ1x-тоже решение ОЛДУ-n. L(xk-1 eλ1x)=0+0+…+0=0 следовательно xk-1 eλ1x тоже решение ОЛДУ-n. Вывод: Если λ1-как кратный корень ХУ, то ему соответствует ,,к,, решений:
y1= eλ1x,y2=x eλ1x,y3=x2 eλ1x,…,yk=xk-1 eλ1x –входят в ФСР как лин. независимые
4. Среди корней ХУ имеются почленно сопряжённые как кратные корни λ1,2=α+iβк р “ к” Всего 2к корней. Следует 2 кратным корнем имеет два вещественные решения y1= eαxcosβx,y2= eαxsinβx
В силу кратности y3=x eαxcosβx,…,y2k-1=xk-1 eαxcosβx
y4=x eαxsinβx,…, y2k=xk-1 eαxsinβx
Дата добавления: 2018-02-15; просмотров: 398; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
