ДУ первого порядка: основные понятия и определения. Теорема о существовании и единственности задачи Коши для ДУ-1(без док-ва)
Решение уравнения с разделяющимися переменными
Понятие однородной функции n-ого измерения однородные ДУ-1, их решение
Линейные ДУ-1: определение, отыскание общего решения методом Бернулли.
ДУ-1 Бернулли: определение, отыскание общего решения
Основные понятия и определения
1. Дифференциальным уравнением (ДУ) порядка “n” называется уравнение , связывающее аргумент х, функцию y и ее производные функции.
F(x,y,y',y'',..y(n))=0
2. Старшая производная задана неявно.
3.Порядок старшей производной – порядок ДУ.
4.Если у=у(х), то ДУ- обыкновенное. Если у=у(x,t,ω), то F(x,t,ω, 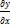 ,
, 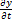 ,
, 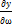 )=0-уравнение в частных производных.
)=0-уравнение в частных производных.
5. у=у(х)-решение ДУ, если при подстановке в ДУ получаем тождество.
6. у=у(х,С1, С2….Сn) , где С1, С2….Сn- произвольные постоянные- общее решение.
7. у=у(х), х=х(у) удовлетворяющее этому ДУ, но не входящие в общее решение- особое решение
8. Если в общем решении у=у(х,С1, С2….Сn) произвольным постоянным придать конкретное значение, то имеем частное решение.
9. Отыскание решения - интегрирование ДУ.
10. Если решение ДУ записано через интегралы, то говорят, что решение – квадратуры(даже если интегралы неберущиеся)
Теорема о существовании и единственности задачи Коши для ДУ-1(без док-ва)

 у а)Пусть дано уʹ=f(x,y): 1. Д-область существования f(x,y)
у а)Пусть дано уʹ=f(x,y): 1. Д-область существования f(x,y)
2. f(x,y), 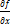 непрерывны в Д, тогда для всякого (х0,у0)
непрерывны в Д, тогда для всякого (х0,у0)
|
|
|
 х существует решение у=у(х), такое что у(х0)=у0
х существует решение у=у(х), такое что у(х0)=у0
б) Если решениям ДУ-1 у=у1(х) и у=у2(х) совпадают в одной точке, то они тождественны.
Решение уравнения с разделяющимися переменными
уʹ=f(x)*g(y)
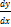 = f(x)*g(y) |*
= f(x)*g(y) |* 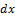
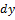 = f(x)*g(y)*
= f(x)*g(y)* 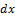 |/g(y)≠0
|/g(y)≠0
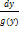 = f(x)*
= f(x)* 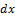
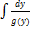 =
= 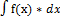 - общее решение
- общее решение
Понятие однородной функции n-ого измерения однородные ДУ-1, их решение
f(x,y)- однородная измерения m, если f(tx, ty)=tm*f(x, y)
Метод решения однородного ДУ-1:
f(x, y)=f(tx, ty)
уʹ= f(x, y)=f(tx, ty) => уʹ= f(tx, ty)
Пусть t= 
уʹ= f(  *x,
*x,  *y)=f(1,
*y)=f(1,  )
)
уʹ= f(1,  ) =>однородное ДУ-1 можно сделать зависимым только от отношения
) =>однородное ДУ-1 можно сделать зависимым только от отношения  (
(  ) (5)
) (5)
 =u(x)
=u(x)
y=u(x)*x
уʹ= 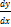 =
= 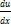 *x+u (6)
*x+u (6)
(6) в (5): 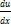 *x+u= f(1, u) – ДУ-1 с разделяющимися переменными.
*x+u= f(1, u) – ДУ-1 с разделяющимися переменными.
Вывод: однородные ДУ-1 подстановкой  =u(x) сводятся к уравнению с разделяющимися переменными.
=u(x) сводятся к уравнению с разделяющимися переменными.
Линейные ДУ-1: определение, отыскание общего решения методом Бернулли.
Если q(x) 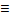 0 для всякого х
0 для всякого х 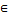 Д, то уʹ+p(x)*y=0- однородное линейное ДУ-1.
Д, то уʹ+p(x)*y=0- однородное линейное ДУ-1.
Если q(x) 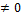 , то уʹ+p(x)*y= q(x)- неоднородное линейное ДУ-1.
, то уʹ+p(x)*y= q(x)- неоднородное линейное ДУ-1.
общего решения методом Бернулли
у=u(x)*v(x) (10)
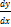 =
= 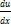 *v+u*
*v+u* 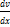
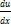 *v+u*
*v+u* 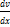 +p(x)*u*v= q(x)
+p(x)*u*v= q(x)
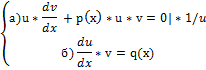
a) 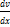 =- p(x)*v |*
=- p(x)*v |* 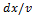
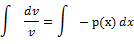
v= 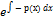 (11)
(11)
Подставим v в б:
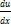 *
* 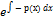 =q(x) |*
=q(x) |* 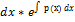
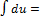
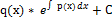
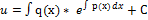 (12)
(12)
Ответ: (11), (12) в (10)
ДУ-1 Бернулли: определение, отыскание общего решения
|
|
|
уʹ+p(x)*y= q(x)*уm|/ уm≠0
m≠0
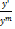 + p(x)*
+ p(x)* 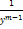 = q(x)
= q(x)
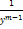 = z
= z
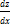 =
= 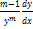 =>
=> 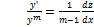 =>
=> 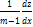 + p(x)*z = q(x) –НЛДУ-1
+ p(x)*z = q(x) –НЛДУ-1
Замечание: у=u*v – подстановка.
Дифференциальные уравнения высшего порядка: основные понятия и определения. Три типа ДУ высшего порядка, допускающие понижение порядка.
Основные понятия и определения.
10 ДУ- уравнение связывающее независимую переменную х с искомой функцией y(x)и её производными
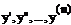 .
.
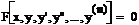 (1)
(1)
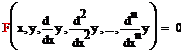 (1)
(1)
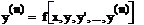 (2)
(2)
(1) – ДУ – неразрешённое относительно старшей производной
(2) – ДУ – разрешённое относительно старшей производной y(n)(в нормальном виде)
20 Порядок старшей производной называется порядком ДУ
30 y=y(x), то ДУ называется обыкновенным
40 y=y(x, t, ω)
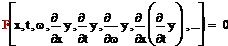 - уравнение в частных производных
- уравнение в частных производных
50 y=y(x)– решение, если при подстановке ДУ получится тождество
60 y=y(x, C1, C2,…, Cn), где C1, C2,…, Cn– общее решение ДУ-n
70 y=y(x), x=x(y)удовлетворяющие данному ДУ, но не входящие в общее решение, называются особым решением
80 Если в общем решении y=y(x, C1, C2,…, Cn)произвольные постоянные – конкретные значения C1=C01, C2=C02,…, Cn=C0n, то имеем частное решение ДУ
90 Отыскание решений ДУ называется интегрированием ДУ
«решить ДУ», «проинтегрировать ДУ» - синонимы
100 Если решение ДУ записано через интеграл, то говорят, что решение найдено в квадратурах, даже, если эти интегралы не выражены в элементарных функциях
|
|
|
Ф(x, y, C1, C2,…, Cn)=0– общий интеграл
y=y(x, C1, C2,…, Cn)– общее решение
Дата добавления: 2018-02-15; просмотров: 570; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
