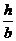Геометрические характеристики плоских фигур – основные понятия, определения положения центра фигуры.
Кручение стержня прямоугольного поперечного сечения (закон распределения напряжений по сечению, зависимости для определения напряжений и перемещений).
При кручении прямоугольных стержней гипотеза плоских сечений не выполняется, так как сечения искривляются - депланируют. Задача о кручении прямоугольных стержней решается в теории упругости.
Готовые формулы
h>b
Рис. 8.5 Эпюра касательных напряжений для некруглых стержней
В углах и центре тяжести 0
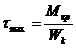
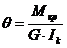
где Wk = a×b2×h - момент сопротивления при кручении
Ik = b×b3×h -
a, b, g -коэффициенты, зависят от соотношения 
Некоторые значения коэффициентов a, b, g.
|
| |||||||
| 1 | 1,5 | 1,75 | 2 | 2,5 | 3 | 10 | |
| a | 0,208 | 0,231 | 0,239 | 0,246 | 0,256 | 0,267 | 0,313 |
| b | 0,141 | 0,196 | 0,214 | 0,229 | 0,249 | 0,263 | 0,313 |
| g | 1 | 0,869 | 0,82 | 0,795 | 0,766 | 0,753 | 0,742 |
Абсолютный угол закручивания вала, состоящего из n участков - j.
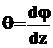
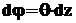
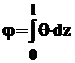
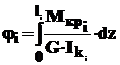
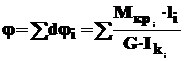
Понятия о стесненном и свободном кручении.
Стесненное кручение
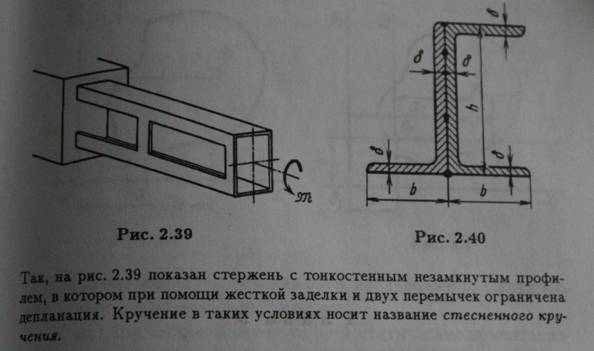
Свободное кручение
В стержнях некруглого сечения при кручении сечения не остаются плоскими, а искривляются (депланируют).
Если для такойдепланации нет никаких препятствий, то в поперечных сечениях нормальных напряжений не возникает. Такое кручение называется чистым или свободным.
Свободное кручение возможно лишь при условии, что сечение стержня и крутящий момент постоянны, а концы стержня не заделаны.
Потенциальная энергия деформации и работа внешних нагрузок при кручении.
|
|
|
При кручении внешние моменты, приложенные к валу, совершают работу вследствие поворота сечений, к которым они приложены. Эта работа расходуется на создание запаса потенциальной энергии деформации, численно равной работе внутренних сил.
В пределах упругих деформаций согласно закону Гука угол закручивания растет пропорционально крутящему моменту. Поэтому зависимость крутящ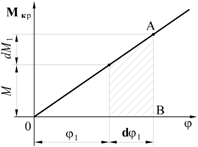 
его момента от угла закручивания 
представляет собой прямую ОА, изображенную на рисунке 11.3. Пусть угол 
соответствует промежуточному значению М. Увеличим момент
Рисунок 11.3 на бесконечно малую величину dM. Тогда угол получит приращение dj.
Произведенная работа равна площади заштрихованной трапеции и определится соотношением
(11.10)
Полная работа деформации при возрастании крутящего момента от 0 до Мкр, равная накопленной потенциальной энергии, представится площадью треугольника 
и будет равна
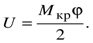(11.11)
Подставим в формулу (11.11) значение угла закручивания
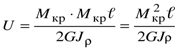; (11.12)
Получено выражение потенциальной энергии при кручении
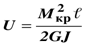
где G – модуль сдвига;
– полярный момент инерции сечения;
l – длина вала.
Потенциальная энергия может быть выражена и через деформацию, если в формулу (11.12) подставить зависимость крутящего момента от угла закручивания.
Поскольку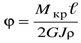 
, то 
.
Таким образом, потенциальная энергия равна
|
|
|
; 
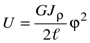. (11.13)
Геометрические характеристики плоских фигур – основные понятия, определения положения центра фигуры.
Рассмотрим некоторое поперечное сечение в системе координат x, y
И два следующих интеграла.
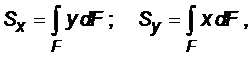
Каждый из этих интегралов представляет собой сумму произведений элементарных площадей dF на расстояние до соответствующей оси (x или y). Первый интеграл называется статическим моментом сечения относительно оси x, а второй – статическим моментом сечения относительно оси y.
При параллельном переносе осей статический моменты изменяются. Рассмотрим 2 пары параллельных осей x1, у1 и х2, у2. Пусть а и b – расстояния между осями х1 и х2, у1 и у2 соответственно (см рис). Положим, что площадь сечения F и статические моменты относительно осей х1 и у1, т.е. Sx1 и Sy1 , заданы. Требуется определить Sx2 и Sy2.
Очевидно х2=х1-a, y2=y1-b. Искомые статические моменты будут равны.
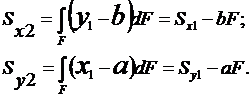
Т.о., при параллельном переносе осей статический момент изменяется на величину, равную произведению площади F на расстояние между осями.
Рассмотрим детально, например, первое из полученных выражений:
|
|
|
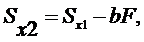
Величина b может быть любой: как положительной, так и отрицательной. Поэтому её всегда можно подобрать (причём единственным образом) так, чтобы произведение bF было равно Sx1 . Тогда статический момент Sx2 , относительно оси x2 обращается в ноль.
Ось, относительно которой статический момент равен нулю, называется центральной.
Моменты инерции сечения
В дополнении к статическим моментам рассмотрим ещё три следующих интеграла:
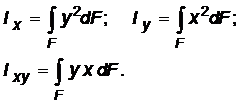
Где по прежнему через х и у обозначены текущие координаты элементарной площадки dF в произвольно взятой системе координат xOy. Первые 2 интеграла называются осевыми моментами инерции сечения относительно осей х и у соответственно. Третий интеграл называется центробежным моментом инерции сечения относительно х, у. Осевые моменты всегда положительны, т.к. положительной считается площадь dF. Центробежный момент инерции может быть как положительным, так и отрицательным, в зависимости от расположения сечения относительно осей x, у.
Выведем формулы преобразования моментов инерции при параллельном переносе осей. (см рис). Будем считать, что нам заданы моменты инерции и статические моменты относительно осей х1 и у1. Требуется определить моменты относительно осей х2 и у2.
|
|
|
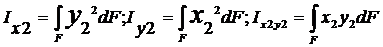
Подставляя сюда x2=x1-a и y2=y1-b Находим
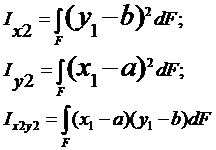
Раскрывая скобки, имеем.
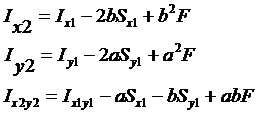
Если оси х1 и у1 – центральные, то Sx1= Sy1=0 и полученные выражения упрощаются:
При параллельном переносе осей (если одна из осей – центральная) осевые моменты инерции изменяются на величину, равную произведению площади сечения на квадрат расстояния между осями.
Дата добавления: 2018-02-15; просмотров: 1658; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!