Случайные величины задают законами распределения.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Закон распределения случайной величины- это соответствие, установленное между возможными значениями случайной величины и их вероятностями.Законы распределения могут быть заданы тремя способами: табличным, графическим, аналитическим. Способ задания зависит от типа случайной величины.

Различают два основных типа случайных величин: дискретные и непрерывно распределенные случайные величины.

Дискретная и непрерывная случайные величины

Если значения, которые может принимать данная случайная величина , образует дискретный (конечный или бесконечный) ряд чисел 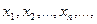то и сама случайная величина называется дискретной. Если же значения, которые может принимать данная случайная величина , заполняют конечный или бесконечный промежуток (а, в) числовой оси Ох, то случайная величина называется непрерывной.

Закон распределения случайной величины

Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.

Закон распределения дискретной случайной величины обычно задается рядом распределения:

				…
				…

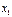
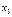
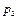
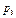
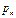
При этом 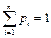, где суммирование распространяется на все (конечное или бесконечное) множество возможных значений данной случайной величины .

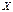Задача 1. Даны вероятности значений случайной величины : значение 10 имеет вероятность 0,3; значение 2 – вероятность 0,4; значение 8 – вероятность 0,1; значение 4 – вероятность 0,2. Построить ряд распределения случайной величины .

Решение. Расположив значения случайной величины в возрастающем порядке, получим ряд распределения:

	2	4	8	10
	0,4	0,2	0,1	0,3

Возьмем на плоскости хОр точки (2; 0,4), (4; 0,2), (8; 0,1) и (10; 0,3). Соединив последовательные точки прямолинейными отрезками, получим многоугольник (или полигон) распределения случайной величины

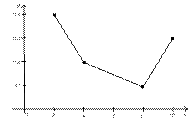
Задача 2. Разыгрываются две вещи стоимостью по 5000 руб и одна вещь стоимостью 30000 руб. Составить закон распределения выигрышей для человека, купившего один билет из 50.

Решение. Искомая случайная величина представляет собой выигрыш и может принимать три значения: 0, 5000 и 30000 руб. Первому результату благоприятствует 47 случаев, второму результату - два случая и третьему – один случай. Найдем их вероятности: ; ; .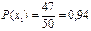

Закон распределения случайной величины имеет вид:

	0	5000	30000
	0,94	0,04	0,02

В качестве проверки найдем .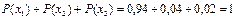

Биномиальное распределение

Пусть производится определенное число n независимых опытов, причем в каждом из них с одной и той же вероятностью может наступить некоторое событие Р. Рассмотрим случайную величину , представляющую собой число наступлений событий A в n опытах. Закон ее распределения имеет вид

Значения	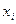0	1	2	…	n
Вероятности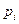

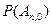
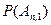
Где , вычисляется по формуле Бернулли.

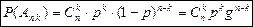
Закон распределения, который характеризуется такой таблицей, называется биноминальным.

Задача. Монету подбрасывают 5 раз. Составить закон распределения случайной величины - числа выпадения герба.

Решение. Возможны следующие значения случайной величины 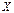: 0, 1, 2, 3, 4, 5. Зная, что вероятность выпадения герба в одном испытании равна , найдем вероятности значений случайной величины 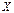по формуле Бернулли:

; ;

; .

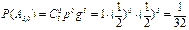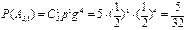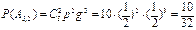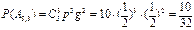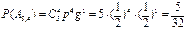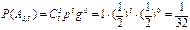Закон распределения имеет вид

Значения	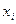0	1	2	3	4	5
Вероятности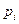

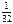
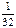
Сделаем проверку: .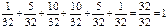

Математическое ожидание и дисперсия случайной величины.

Математическое ожидание дискретной случайной величины

Наиболее исчерпывающей характеристикой случайной величины является ее закон распределения вероятностей. Однако не всегда обязательно знать весь закон распределения. Иногда можно обойтись одним или несколькими числами, отражающими наиболее важные особенности закона распределения, например, числом, имеющим смысл «среднего значения» случайной величины, или же числом, показывающим средний размер отклонения случайной величины от своего среднего значения. Такого рода числа называются числовыми характеристиками случайной величины. Оперируя числовыми характеристиками, можно решать многие задачи, не пользуясь законом распределения.

Одна из самых важных числовых характеристик случайной величины есть математическое ожидание.

Если известна дискретная случайная величина , закон распределения которой имеет вид

Значения			…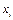
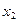
Вероятности			…

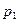
то математическим ожиданием (или средним значением) дискретной величины называется число

Таким образом, математическое ожидание дискретной случайной величины равно сумме произведений возможных значений этой величины на их вероятности.

Пример 1. Найти математическое ожидание случайной величины , зная закон ее распределения

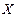
	-1	0	1	2	3
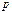
	0,2	0,1	0,25	0,15	0,3

Решение.

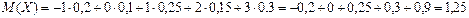Свойства математического ожидания.

1. Постоянный множитель можно выносить за знак математического ожидания:

2. Математическое ожидание постоянной величины С равно самой этой величине: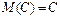

3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий: .

4. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих величин: .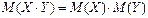

Среднее квадратичное отклонение и дисперсия случайной величины.

Пример 2. Найдем математическое ожидание случайных величин и , зная законы их распределения

	-8	-4	-1	1	3	7
	1/12	1/6	1/4	1/6	1/12	1/4

	-2	-1	0	1	2	3
	1/6	1/6	1/12	1/3		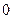1/4

Решение: , .

Получили любопытный результат: законы распределения величин

разные, а их математические ожидания одинаковы.

б)

Из рисунка б видно, что значение величины более сосредоточены около математического ожидания , чем значения величины , которые разбросаны (рассеяны) относительно ее математического ожидания (рисунок а).

Основной числовой характеристикой степени рассеяния значений случайной величины относительно ее математического ожидания является дисперсия, которая обозначается через .

Определение.Отклонением называется разность между случайной величиной и ее математическим ожиданием , т.е. .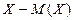

Отклонение 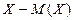и его квадрат 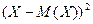также являются случайными величинами.

Определение. Дисперсией дискретной случайной величины называется математическое ожидание квадрата ее отклонения: .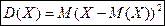

Свойства дисперсии.

1. Дисперсия постоянной величины С равна 0: .

2. Если - случайная величина, а С – постоянная, то , .

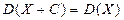3. Если и - независимые случайные величины, то .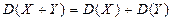

Для вычисления дисперсий более удобной является формула .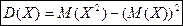

Пример 3. Дискретная случайная величина распределена по закону:

	-1	0	1	2
	0,2	0,1	0,3	0,4

Найти .

Решение. Сначала находим . ,

а затем . .

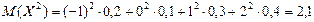По формуле 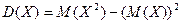имеем .

Средним квадратичным отклонением случайной величины называется корень квадратный из ее дисперсии: .

Содержание работы.

Задание 1. Используя классическое определение вероятности, решите задачи:

1.1. В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.

1.2. Брошена игральная кость. Найти вероятность того, что выпадет четное число очков.

1.3. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.

1.4. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиков можно будет прочесть слово «спорт».

1.5. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь одну окрашенную грань

Задание 2. Используя теорему сложения вероятностей, решите задачи:

2.1. В денежно-вещевой лотерее на каждые 10 000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного лотерейного билета?

2.2. Вероятность того, что стрелок при одном выстреле выбьет 10 очков, равна 0,1; вероятность выбить 9 очков равна 0,3; вероятность выбить 8 или меньше очков равна 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков.

2.3. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2 деталей есть хотя бы одна стандартная.

2.4. В ящике 10 деталей, среди которых 2 нестандартных. Найти вероятность того, что в наудачу отобранных 6 деталях окажется более одной нестандартной детали.

2.5. События А, В, С и D образуют полную группу. Вероятности событий таковы: Р(А)=0,1; Р(В) = 0,4; Р(С)=0,3. Чему равна вероятность события D?

Задание 3. Используя теорему умножения вероятностей, решите задачи:

3.1. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго – 0,8, для третьего – 0,9. Определите вероятность того, что в цель попадет хотя бы один стрелок.

3.2. Вероятность того, что стрелок при одном выстреле попадет в мишень, равна р=0,9. Стрелок произвел три выстрела. Найти вероятность того, все 3 выстрела дали попадание.

5.3. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго – 0,8, для третьего – 0,9. Определите вероятность того, что все три стрелка одновременно попадут в цель.

3.4. В первом ящике имеются 2 белых и 10 черных шаров; во втором ящике 8 белых и 4 черных шара. Из каждого ящика извлекли по шару. Какова вероятность, того, что оба шара белые?

3.5. Брошены монета и игральная кость. Найти вероятность совмещения событий: «появился «герб», «появилось 6 очков».

Задание 4. Найдите математическое ожидание дискретной случайной величины X, заданной законом распределения:

4.1

	4	6	10
	0,2	0,3	0,5

4.2

	0,21	0,54	0,61
	0,1	0,5	0,4

4.3

	0,2	0,5	0,6
	0,1	0,5	0,4

4.4

	21	54	61
	0,2	0,3	0,5

4.5

	2	5	6
	0,4	0,5	0,1

Задание 5. Найдите математическое ожидание случайной величины Z, если известны математические ожидания X и Y:

5.1

5.2

5.3.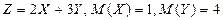

5.4.

5.5.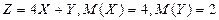

Задание 6. Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины X, заданной законом распределения:

6.1

	130	140	160	180
	0,05	0,10	0,25	0,6

6.2

	50	20	30	40
	0,4	0,3	0,1	0,2

6.3

	550	200	30	40
	0,3	0,4	0,1	0,2

6.4

	60	200	30	40
	0,1	0,6	0,1	0,2

6.5

	60	100	30	40
	0,15	0,55	0,1	0,2

Вопросы для самоконтроля.

Дата добавления: 2021-06-02; просмотров: 236; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!