Теорема сложения вероятностей.

Практическая работа

Тема практической работы: Решение задач на определение вероятности. Построение по заданному условию закона распределения ДСВ и нахождение её математического ожидания и дисперсии.

Цель занятия: научиться решать простейшие задачи на определение вероятности, научиться вычислять закон распределения ДВС, научиться определять числовые характеристики ДВС.

Студент должен:

знать:

- понятия события, частоты и вероятности появления событий, совместных и несовместных событий, полной вероятности;

- теорему сложения вероятностей;

- теорему умножения вероятностей;

- определение математического ожидания, дисперсии дискретной случайной величины;

- понятие среднего квадратичное отклонение случайной величины;

уметь:

- находить вероятность в простейших задачах, используя классическое определение вероятностей;

- решать задачи с применением теоремы сложения вероятностей для несовместных событий;

- находить математическое ожидание и дисперсию случайной величины по заданному закону ее распределения;

- находить среднее квадратичное отклонение случайной величины.

Оборудование:

1. Условие «Практической работы № 10».

2. Микрокалькулятор.

Справочный материал

Понятие о случайном событии. Виды событий. Вероятность события.

Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, будем называть испытанием. Результат этого действия или наблюдения называется событием. Если событие при заданных условиях может произойти или не произойти, то оно называется случайным. В том случае, когда событие должно непременно произойти, его называют достоверным, а в том случае, когда оно заведомо не может произойти,- невозможным.События называются несовместными, если каждый раз возможно появление только одного из них.События называются совместными, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании.События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны.События принято обозначать заглавными буквами латинского алфавита: А, В, С, Д, … . Полной системой событий А₁, А₂, А₃, … , А_n называется совокупность несовместных событий, наступление хотя бы одного из которых обязательно при данном испытании.

Если полная система состоит из двух несовместных событий, то такие события называются противоположными и обозначаются А и .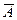

Пример. В коробке находится 30 пронумерованных шаров. Установить, какие из следующих событий являются невозможными, достоверными, противоположными: достали пронумерованный шар (А); достали шар с четным номером (В); достали шар с нечетным номером (С); достали шар без номера (Д). Какие из них образуют полную группу?

Решение. А - достоверное событие; Д - невозможное событие; В и С - противоположные события.

Полную группу событий составляют А и Д, В и С.

Вероятность события, рассматривается как мера объективной возможности появления случайного события.

Классическое определение вероятности

Число, являющееся выражением меры объективной возможности наступления события, называется вероятностью этого события и обозначается символом Р(А).

Определение.Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению данного события А, к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е. 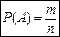. Следовательно, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, подсчитать все возможные несовместные исходы n , выбрать число интересующих нас исходов m и вычислить отношение m к n.

Из этого определения вытекают следующие свойства:

1. Вероятность любого испытания есть неотрицательное число, не превосходящее единицы.

Действительно, число m искомых событий заключено в пределах 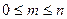. Разделив обе части на n, получим .

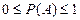2. Вероятность достоверного события равна единице, т.к. .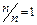

3. Вероятность невозможного события равна нулю, поскольку .

Задача 1. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?

Решение. Общее число различных исходов есть n=1000. Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле, получим .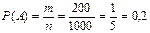

Задача 2. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найти вероятность того, что из этих 5 деталей две окажутся бракованными.

Решение. Число всех равновозможных независимых исходов n равно числу сочетаний из 18 по 5 т.е.

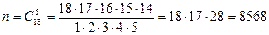
Подсчитаем число m, благоприятствующих событию А. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2: .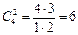

Число способов выборки трех качественных деталей из 14 имеющихся качественных равно .

Любая группа качественных деталей может комбинироваться с любой группой бракованных деталей, поэтому общее число комбинаций m составляет .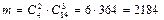

Искомая вероятность события А равна отношению числа исходов m, благоприятствующих этому событию, к числу n всех равновозможных независимых исходов: .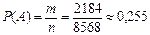

Теорема сложения вероятностей несовместных событий

Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них.

Сумму двух событий обозначают символом А+В, а сумму n событий символом А₁+А₂+ … +А_n.

Теорема сложения вероятностей.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

или

Следствие 1. Если событие А₁, А₂, … ,А_n образуют полную систему, то сумма вероятностей этих событий равна единице. .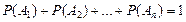

Следствие 2. Сумма вероятностей противоположных событи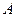й и 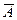равна единице. .

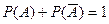Задача 1. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20000 руб., на 10 - по 15000 руб, на 15 - по 10000 руб., на 25 - по 2000 руб. и на остальные ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не менее 10000 руб.

Решение. Пусть А, В, и С- события, состоящие в том, что на купленный билет падает выигрыш, равный соответственно 20000, 15000 и 10000 руб. так как события А, В и С несовместны, то

Задача 2. На заочное отделение техникума поступают контрольные работы по математике из городов А, В и С. Вероятность поступления контрольной работы из города А равна 0,6, из города В - 0,1. Найти вероятность того, что очередная контрольная работа поступит из города С.

Решение. События «контрольная работа поступила из города А», «контрольная работа поступила из города В» и «контрольная работа поступила из города С» образуют полную систему, поэтому сумма их вероятностей равна единице: 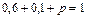, т.е. .

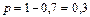Задача 3. Вероятность того, что день будет ясным, 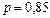. Найти вероятность того, что день будет облачным.

Решение. События «день ясный» и «день облачный» противоположные, поэтому

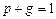, т.е .

Теорема умножения вероятностей независимых событий

При совместном рассмотрении двух случайных событий А и В возникает вопрос:

Как связаны события А и В друг с другом, как наступление одного из них влияет на возможность наступления другого? Простейшим примером связи между двумя событиями служит причинная связь, когда наступление одного из событий обязательно приводит к наступлению другого, или наоборот, когда наступление одного исключает возможность наступления другого. Для характеристики зависимости одних событий от других вводится понятие условной вероятности.

Определение. Пусть А и В - два случайных события одного и того же испытания. Тогда условной вероятностью события А или вероятностью события А при условии, что наступило событие В, называется число . Обозначив условную вероятность , получим формулу , .

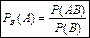Задача 1. Вычислить вероятность того, что в семье, где есть один ребенок- мальчик, родится второй мальчик.

Решение. Пусть событие А состоит в том, что в семье два мальчика, а событие В - что один мальчик.

Рассмотрим все возможные исходы: мальчик и мальчик; мальчик и девочка; девочка и мальчик; девочка и девочка. Тогда 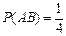, и по формуле находим .

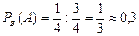Событие А называется независимым от события В, если наступление события В не оказывает никакого влияния на вероятность наступления события А.

Теорема умножения вероятностей. Вероятность одновременного появления двух независимых событий равна произведению вероятностей этих событий: 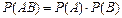. Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле .

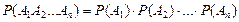Задача 1. В первой урне находится 6 черных и 4 белых шара, во второй- 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми.

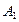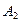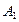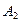Решение. Пусть - из первой урны извлечен белый шар; - из второй урны извлечен белый шар. Очевидно, что события и независимы. Так как , , 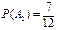то по формуле находим. .

Задача 2. Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Найти вероятность того, что: а) оба элемента выйдут из строя; б) оба элемента будут работать.

Решение. Пусть событие А- выход из строя первого элемента, событие В- выход их строя второго элемента. Эти события независимы (по условию).

а) Одновременное появление А и В есть событие АВ. Следовательно, .

б) Если работает первый элемент, то имеет место событие 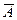(противоположное событию А- выходу этого элемента из строя); если работает второй элемент- событие В. Найдем вероятности событи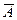й и :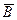

; .

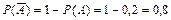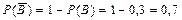Тогда событие, состоящее в том, что будут работать оба элемента, есть 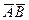и, значит,

Случайная величина, ее функция распределения.

Случайная величина, способы ее задания.

Случайной называется величина, которая в результате испытания может принять то или иное числовое значение, причем заранее неизвестно, какое именно. Если случайное событие - качественная характеристика испытаний, то случайная величина - его количественная характеристика. Случайные величины обозначают заглавными латинскими буквами 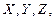а их значение – прописными- . 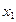Вероятность того, что случайная величина примет значение обозначают: 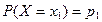и т.д.

Дата добавления: 2021-06-02; просмотров: 130; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!