Треугольник. Формулы. Площадь
| Треугольник называется равнобедренным, если две стороны его равны | ||
| В равнобедренном треугольнике углы при основании равны | ||
| Если два угла треугольника равны, то треугольник равнобедренный | ||
| В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой | ||
| Сумма углов треугольника равна 180˚ | ||
| Стороны треугольника пропорциональны синусам противолежащих углов (теорема синусов) | ||
| Отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности (или двум радиусам) | ||
| Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними (обобщенная теорема Пифагора, теорема косинусов) | ||
Основное тригонометрическое тождество 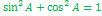
| ||
| Площадь треугольника равна половине произведения его основания на высоту | ||
S= 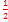 a·h; P= a+b+c a·h; P= a+b+c
| ||
| Если высоты двух треугольников равны, то их площади относятся как основания | ||
| Если угол одного треугольника равен углу другого треугольника, то их площади относятся как произведения сторон, заключающих равные углы | ||
Площадь S треугольника со сторонами a,b,c выражается формулой
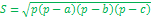 , где , где 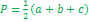 - полупериметр треугольника (формула Герона) - полупериметр треугольника (формула Герона)
| ||
| Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности | ||
| Площадь треугольника равна половине произведения двух сторон на синус угла между ними | ||
| В любой треугольник можно вписать окружность (только одну) Около любого треугольника можно описать окружность (только одну) |
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
| Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны - катетами | ||
| В прямоугольном треугольнике гипотенуза больше катета | ||
| Сумма двух острых углов прямоугольного треугольника равна 90˚ | ||
| Катет прямоугольного треугольника, лежащий против угла в 30˚, равен половине гипотенузы. /Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равен 30˚, | ||
| Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны. | ||
| Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному. | ||
| Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой. | ||
| Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. | ||
| Площадь прямоугольного треугольника равна половине произведения основания на высоту | ||
| В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора) /Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. | ||
| Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе | ||
| Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе | ||
| Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету | ||
| Тангенс угла равен отношению синуса к косинусу этого угла | ||
| Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны. |
Справочник по геометрии
Дата добавления: 2021-06-02; просмотров: 50; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
