ГЛАВА 2. ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ
ВВЕДЕНИЕ
Основной задачей в настоящее время является развитие ребенка. Перед учителем ставится задача раскрыть индивидуальные способности ребенка, творческие возможности. Благодаря постоянным занятиям, упражнениям ученик получает определенные знания, умения и навыки. Чтобы занятия проходили интересно, с привитием новых знаний учителю необходимо постоянно повышать свои знания, уметь профессионально владеть информационными технологиями, владеть различными формами и методами обучения.
При обучении геометрических фигур, кривых на уроках математики преподавателю необходимо создать у учеников правильные геометрические образы, развить пространственные представления, вооружить их навыками черчения и измерения, сравнения, анализа, которые имеют большое жизненно - практическое значение.
Знакомство с кривыми и изучение их свойств углубит знания, геометрические представления, повысит интерес к геометрии; создаст содержательную основу для дальнейшего изучения математики, физики и других наук, поэтому данная работа актуальна в настоящее время.
Объектом исследования являются кривые, окружность, круг.
Цель исследования: рассмотреть кривые, замечательные кривые, окружность и круг, примеры и их свойства.
В ходе работы можно выделить следующие задачи:
- рассмотреть виды кривых и их свойства;
- замечательные кривые и их применение;
- окружность и круг;
|
|
|
Работа состоит из введения, глав, заключения, списка использованных источников. В ходе написания работы использовалась современная литература.
ГЛАВА 1. ВИДЫ КРИВЫХ
В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки и иногда определяется как «длина без ширины» или как «граница фигуры». По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и также трансцендентные кривые), применяя в каждом случае специальные приёмы.
Рассмотрим следующие виды кривых.
Кривые первого порядка
Линия первого порядка на плоскости определяется алгебраическим уравнением первой степени относительно декартовых координат x и y:
Ax+By + C = 0 (1)
Уравнение (1) определяет прямую на плоскости.
Кривые второго порядка
Кривой второго порядка называется линия, уравнение которой в декартовой системе координат имеет вид: 
(2)
где хотя бы один из коэффициентов A, B, C не равен нулю.
|
|
|
Уравнение (2) определяет кривую линию, которая называется кривой второго порядка. Это может быть окружность, эллипс, гипербола, парабола и их вырождения.
Рассмотрим кривые второго порядка.
1. Окружность.
Окружностью называется геометрическое место точек M(x, y) плоскости, расстояние которых до данной точки A(a, b) этой плоскости (называемой центром этой окружности) есть величина постоянная R - радиус окружности (рисунок 1).
Рисунок 1 – Окружность
Уравнение окружности имеет вид 
.
При a=b=0 получим уравнение окружности с центром в начале координат: 
. При R = 0 данные окружности вырождаются в точки с координатами соответственно (a, b) и (0, 0).
2. Эллипс
Эллипсом называется геометрическое место точек M(x, y) плоскости, сумма расстояний которых до двух данных точек F1 и F2 этой плоскости (называемых фокусами этого эллипса) есть величина постоянная (рисунок 2).
Рисунок 2 – Эллипс
Уравнение 
называется каноническим уравнением эллипса, где a - большая полуось, b - малая полуось эллипса.
Вырождения эллипса:
1.уравнение 
определяет мнимый эллипс;
2.уравнение 
представляет точку с координатами (0, 0).
Свойства эллипса:
1. Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.
|
|
|
2. Эллипс имеет две взаимно перпендикулярные оси симметрии.
3. Эллипс может быть получен сжатием окружности.
3. Гипербола
Гиперболой называется геометрическое место точек M(x, y) плоскости, разность расстояний которых до двух данных точек F1 и F2 этой плоскости (называемых фокусами этой гиперболы) есть величина постоянная (рисунок 3).
Рисунок 3 - Гипербола
Уравнение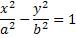 
называется каноническим уравнением гиперболы, где a- действительная ось, b - мнимая ось гиперболы.
Уравнение 
представляет сопряжённую с данной гиперболу.
Вырождения гиперболы:
или 
Имеем пару пересекающихся прямых: 
и 
Свойства гиперболы:
Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (–a; 0), которые называются вершинами гиперболы.
Гипербола имеет две взаимно перпендикулярные оси симметрии.
Гипербола имеет центр симметрии.
4. Парабола
Параболой называется геометрическое место точек M(x, y) плоскости, равноотстоящих от данной точки F этой плоскости (называемой фокусом) и данной прямой (называемой директрисой параболы), предполагая, что на ней не лежит эта точка F (рисунок 4).
Рисунок 4 – Парабола
|
|
|
Уравнение 
называется каноническим уравнением параболы, где
p (p > 0) — параметр параболы.
Уравнение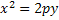 
определяет параболу, симметричную относительно оси Oy.
Вырождения параболы: при p = 0 получим:
1. уравнение 
, которое определяет дважды совмещённую ось Ox;
2. 
есть дважды совмещённая ось Oy.
Свойства параболы:
Парабола - кривая второго порядка.
Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.
Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
Отрезок, соединяющий середину произвольной хорды параболы и точку пересечения касательных к ней в концах этой хорды, перпендикулярен директрисе, а его середина лежит на параболе.
Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб[1].
Кривые третьего порядка
Примером кривой третьего порядка рассмотрим строфоиду.
Алгебраическая кривая в Евклидовой плоскости называется циркулярной,
если она проходит через абсолютные циклические точки. Циркулярная кривая 3-го порядка называется строфоидой, если она имеет двойную узловую точку с ортогональными касательными в этой точке. Неприводимая строфоида с осью симметрии называется прямой (Рисунок 5), без оси симметрии - наклонной или косой (Рисунок 6).
Рисунок 5 – Прямая строфоида
Рисунок 6 – Косая строфоида
Строфоиды могут быть рассмотрены как различные множества точек в евклидовой плоскости с заданными геометрическими свойствами[2].
ГЛАВА 2. ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ
Часто мы не замечаем, что в жизни нас окружает множество кривых. Мы встречаем их в быту, архитектуре, природе. Даже в древнейшие времена уже были использованы при построении различных архитектурных строений знания и свойства о кривых.
Дата добавления: 2021-06-02; просмотров: 122; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!