Теорема о работе силы тяжести
Г. гр.2СПХ-4
Дисциплина Техническакя механика
Преподаватель Самарский В.Т.
Занятие № 20
Тема Динамика. Силы инерции. Принцип даламбера
Цель дидактическая: обучить студентов, давая им систему теоретических знаний, а также практических умений и навыков;
развивать мыслительные способности, их устную и письменную речь, память, воображение, навыки самоорганизации;
содействовать воспитанию нравственных или эстетических убеждений, чувств, волевых и социально-значимых качеств
Рассматриваемые вопросы:
1. История динамики.
2. Метод кинетостатики. Приецип Даламбера.
З. Весом тела называется сила, с которой тело вследствие притяжения Земли действует на опору (или подвес)?
4. Силы инерции в криволинейном движении.
5. Центробежная и центростремительная силы.
6. Работа и мощность.
Учебный материал: лекция, учебники, видеоматериал.
Опорный конспект лекции
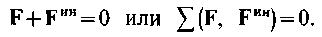Сила инерции есть вектор, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению. Тогда
Это равенство, что является математическим выражением принципа, который носит имя французского ученого Даламбера (1717-1783), можно рассматривать как уравнение равновесия материальной точки. Следует подчеркнуть, что полученное равенство, хотя и названо уравнением равновесия, на самом деле является видоизмененным уравнением движения материальной точки.
|
|
|
Следует отметить, что до Даламбера над общим методом, с помощью которого уравнениям динамики придается форма уравнений статики, работали члены петербургской Академии наук Я. Герман (1716) и Л. Эйлер (1737).
Принцип Даламбера формулируется так: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия.
Следует помнить, что сила инерции приложена к данной материальной точки условно, но для связи, что вызывает ускорение, она в определенном смысле является реальной. Обладая свойством инерции, всякое тело стремится сохранять свою скорость по модулю и направлению неизменной, вследствие чего оно будет действовать на связь, что вызывает ускорение, с силой, равной силе инерции. В качестве примера действия сил инерции можно привести случаи разрушения Маховиков при достижении ими критической угловой скорости. Во всяком вращающемся теле действуют силы инерции, поскольку каждая частица этого тела имеет ускорение, а соседние частицы являются для нее связями.
Поясним это на примере (рис. 14.1). Пусть к телу, лежащему на горизонтальной плоскости, привязана нить, способная выдерживать силу тяжести G этого тела. Если к нити приложить силу R статически (постепенно), то тело будет поднято вверх и нить не оборвется; если силу R приложить динамически (внезапно, рывком), то нить оборвется. Это явление объясняется следующим образом.
|
|
|
Чтобы поднять груз, нужно сообщить ему некое ускорение А. Для определения
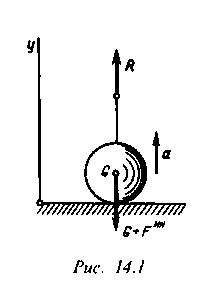
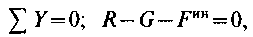величины натяжения нити применим принцип Даламбера и составим уравнение равновесия:
откуда
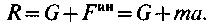
В первом случае груз сообщается небольшое ускорение и сила инерции, что увеличивает натяжение нити, небольшая; во втором случае ускорение, сообщается тело, значительное и сила инерции соответственно возрастает. В обоих случаях сила инерции не увеличивает давление на опору, поскольку приложена к телу условно.
Отметим, что весом тела называется сила, с которой тело вследствие притяжения Земли действует на опору (или подвес), удерживающую его от свободного падения. Если тело и опора неподвижны, то вес тела равен его силе тяжести.
§ 14.2. Силы инерции в криволинейном движении.
В криволинейном движении точки полное ускорение ровно векторной сумме касательного и нормального ускорений
(рис. 14.2).
Касательное ускорение at = dv/dt , нормальне ускорение aп = v2 /δ, полное ускорение
|
|
|
— 
;.
Каждому ускорению соответствует своя сила инерции:
Рин = т•аτ— касательное, или тангециальное;
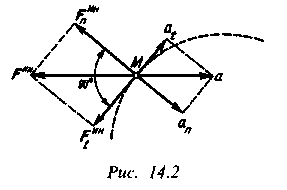
Fп = mv2/δ— нормальное, или центробежное;
Fпн = та — полное.
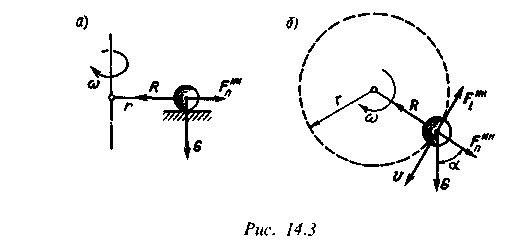
В качестве примера рассмотрим равномерное движение по окружности, лежащей в горизонтальной плоскости, камня силой тяжести G, привязанный к невесомой нити длиной г, расположенной в той же плоскости (рис. 14.3, а). Чтобы нить оставалась в плоскости движения камня, предполагается, что он скользит по идеальной гладкой горизонтальной плоскости. Скорость камня обозначим v. Тогда Fп = mv2/δ— центробежная сила инерции (эта сила натягивает нить); R = mv2/r центростремительная сила, приложенная к камню (эта сила удерживает камень на кругу).
Центробежная и центростремительная силы (действие и противодействие) по третьему закону Ньютона равны по модулю и направлены в противоположные стороны. Очевидно, что касательная сила инерции Fп в этом случае равна нулю, поскольку v = const.
Из опыта известно, что при достаточной скорости нить может разорваться и камень полетит по касательной к окружности, то есть по направлению есть в момент разрыва скорости. Это доказывает, что центробежная сила инерции есть реальная сила для связи, но к телу она приложена условно.
|
|
|
Внутри тел, движущихся с ускорением, также возникают внутренние силы инерции, поскольку для каждой частицы тела соседние частицы являются связями.
Найдем, чему равно натяжение нити, если камень движется по окружности, лежащей в вертикальной плоскости (рис. 14.3, б). Для определения натяжения R нити применим принцип Даламбера, т. е. приложен к камню нормальную силу инерции F"H и касательную силу инерции F,H.
Спроектируем все силы на направление нити, вследствие чего получим 
откуда
По теореме о проекции скорости на координатную ось
Итак, проекция скорости точки м на ось х все время остается величиной постоянной, равной
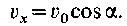
Из двух последних формул имеем
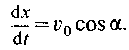
По условию, при t = 0 х = 0, следовательно, произвольная постоянная С2 = 0. Окончательно
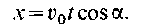
Интегрируя уравнение (13.5), находим
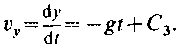
Подставив в это уравнение t = 0, найдём свободную постоянную
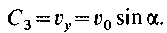
Следовательно
Интегрируя ещё раз, получим:
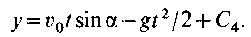
По условию при t = 0 y = 0, следовательно, произвольная постоянная С4 = 0. Окончательно
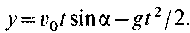
Таким образом, материальная точка М, брошенная со скоростью v0 под углом ос к горизонту, движется согласно
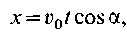
Изменением ускорения свободного падения и сопротивлением воздуха пренебрегать. Радиус Земли считать равным R = 6370 км.
Решение.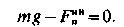 
После того, как ракета-носитель вывела спутник массой т на заданную орбиту и сообщила ему скорость v, касательную к орбите, спутник продолжает движение под действием одной лишь силы тяжести Земли. Для определения скорости г спутника применим принцип Далам-бера, то есть приложенный к спутнику центробежную силу инерции и составим уравнение равновесия, спроецировав силы на ось, что проходит через спутник и центр Земли:
|
|
Поскольку
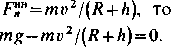
Сократив равенства на т, определим скорость спутника:
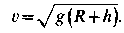
Подставив значения, получим:
Сократив равенство на тЦя скорость, при которой спутник Земли находится на круговой орбите на относительно небольшой высоте, называется первой космической скоростью.
Раздел 15 работа и мощность
§ 15.1. Работа постоянной силы на прямолинейном участке пути
Рассмотрим материальную точку М, к которой приложена в числе прочих сила F. Пусть точка перемещается прямолинейно из положения М0 в положение М1у пройдя путь s (рис. 15.1).
Чтобы установить количественную меру действия силы F на пути s, разложим эту силу на составляет N и R, направлены соответственно перпендикулярно направлению перемещения и вдоль него. Поскольку то, что составляет N не может двигать точку или сопротивляться ее движению в направлении s, то действие силы F на пути s можно определить произведением Rs. Эта новая величина называется работойи обозначается W.
Итак
то есть работа силы равна произведению ее модуля на путь и на косинус угла между направлением силы и направлением перемещения. Таким образом, работа является мерой действия силы, приложенной к материальной точке при некотором ее перемещении.
|
|
Робота — величина скалярная.
|
|
Рассмотрим три отдельные случаи вычисления работы: 1) а = 0, в этом случае W=Fs; 2) а = 90°, в этом случае W=0; 3)a=180°, в этом случае
Итак, работа положительна, если направление силы и направление перемещения совпадают (или а < 90°); работа отрицательна, если направление силы и направление перемещения противоположный (или а > 90°); работа равна нулю, когда направление силы и направление перемещения взаимно перпендикулярное. Так, например, при подъеме тела вверх работа силы тяжести отрицательна, при движении вниз—положительна, а при движении по горизонтальной плоскости работа силы тяжести равна нулю.
Силы, совершающие положительную работу, называются движущими силами, силы совершают отрицательную работу, —силами сопротивления.
Единица работы
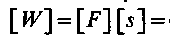
Ньютон·метр=Джоуль (Дж)
Джоуль — это работа силы в один ньютон на пути в один метр (при совпадении направлений силы и перемещения точки ее приложения).
§ 15.2. Работа переменной силы на криволинейном участке пути
На бесконечно малом участке ds криволинейный путь можно считать прямолинейным, а силу — постоянной. Тогда элементарная работа dW на пути ds равна
Работа на конечном перемещении равна сумме элементарных работ:
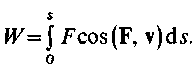
Построим график, выражающий зависимость между /rcos(F, v) и пройденным расстоянием s (рис. 15.2, а).
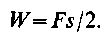
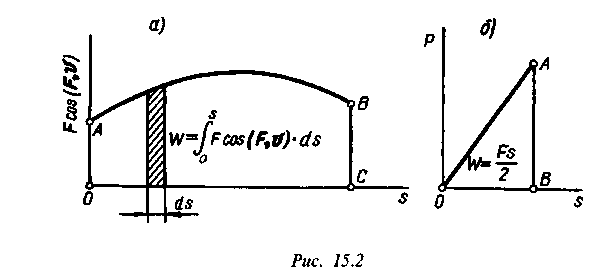Площадь заштрихованной полоски, которую можно принять за прямоугольник, равна элементарной работе на пути ds:
а работа силы F на конечном пути s графически выражается площадью фигуры ОАВС, ограниченной осью абсцисс, двумя ординатами и кривыми АВ, которые называются кривой сил. Если сила совпадает с направлением перемещения и возрастает от нуля пропорционально пути, то работа графически выражается площадью треугольника ОАВ (рис. 15.2, б) и равна половине произведения силы на путь:
§ 15.3. Теорема о работе равнодействующей
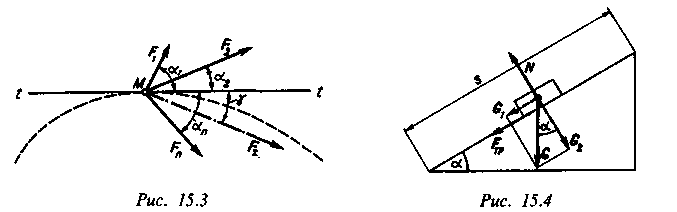Теорема. Работа равнодействующей силы на каком-то участке пути равна сумме алгебры работ сил составляющих на том же участке пути.
Пусть к материальной точке М приложена система сил (Fx, F2, F3 ..., F"), равнодействующая которых равна F1. (рис. 15.3).
Система сил, приложенных к материальной точке, есть система сходящихся сил, следовательно
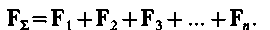
Спроектируем это векторное равенство на касательную к траектории, тогда 
Умножим обе части равенства на бесконечно малое перемещение ds и проинтегрируем это равенство в пределах некоего конечного перемещения s:
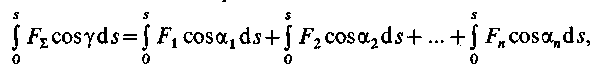
Что даст равенство
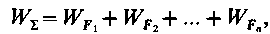
или кратко
Теорема доказана.
Пример 15.1. Вычислить работу, которая производится при равномерном подъеме груза G — 200 Н по наклонной плоскости на расстояние J = 6M, если угол, образуемый плоскостью с горизонтом α = 30°, а коэффициент трения скольжения равен /=0,01 (рис. 15.4).
Решение. Разложим силу тяжести G груза на две взаимно перпендикулярные составляет G1 и G2—соответственно параллельную и перпендикулярную наклонной плоскости. Согласно второму закону трения скольжения, сила трения FTp равна
Применив теорему о работе равнодействующей, вычислим искомую работу как сумму работ сил сопротивления (работа силы G2 и нормальной реакции N равна нулю, так как эти силы перпендикулярны направлению перемещения s):
Подставив значение, получим
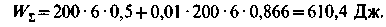
Теорема о работе силы тяжести
Теорема. Работа силы тяжести не зависит от вида траектории и равна произведению модуля силы на вертикальное перемещение точки ее приложения.
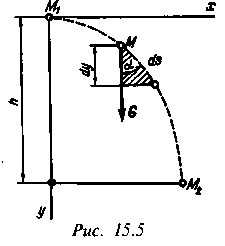
Пусть материальная точка м движется под действием одной лишь силы тяжести G и за какой-то промежуток времени перемещается из положения М1 в положение М2, пройдя путь s (рис. 15.5).
На траектории точки М выделим бесконечно малый участок ds, который считаем прямолинейным, и с его концов проведем прямые, параллельные осям координат, одна из которых вертикальная, а другая горизонтальная. Из заштрихованного треугольника получим, что
Элементарная работа силы G на пути ds равна
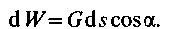
Полная работа на пути s равна
Следовательно
теорема доказана.
Силы, работа которых не зависит от вида траектории, называются потенциальными. К числу таких сил относятся, например, силы тяжести, силы всемирного тяготения, натяжения пружины.
Дата добавления: 2021-05-18; просмотров: 126; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!