Алгоритм для решения системы линейных уравнений методом Гаусса

Методические указания по проведению

Практической работы  

Решение систем линейных алгебраических уравнений различными способами

Цель работы:

 

Используя теоретический материал и образцы решения задач, решить примеры по теме «Решение систем линейных алгебраических уравнений различными способами»

Перечень справочной литературы :

1. Математика: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, С.В. Иволгина; под редакцией В.А. Гусева – 10-е изд., стер. – М.: Издательский центр «Академия». 2014. – 416 с.

2. Элементы высшей математики: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, Ю.А. Дубинский – 9-е изд., стер. – М.: Издательский центр «Академия». 2013. – 320 с.

3. Шипачев В.С. Основы высшей математика: учебник для вузов. -М. Высш.шк., 2010 г.

4. Шипачев В.С. Задачник по высшей математике: учебное пособие для вузов. -М. Высш.шк., 2010 г.

Краткие теоретические сведения

 

1.Пусть дана система линейных уравнений

     (1)

Коэффициенты a₁₁,₁₂,..., a_1n, ... , a_n1 , b₂ , ... , b_n считаются заданными.

Вектор -строка íx₁ , x₂ , ... , x_n ý - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.

  Определитель n-го порядка D=çAê=ça _ij ç, составленный из коэффициентов при неизвестных, называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи:

    a) Если D¹, то система (1) имеет единственное решение, которое может быть найдено по формулам Крамера : x₁= , где

определитель n-го порядка D_i ( i=1,2,...,n) получается из определителя системы путем замены i-го столбца свободными членами b₁ , b₂ ,..., b_n.

    б) Если D= , то система (1) либо имеет бесконечное множество решений , либо несовместна ,т.е. решений нет.

 

2. Рекомендации по выполнению заданий

 

1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.

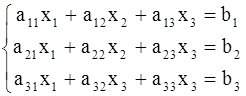    (2).

 

 1. В данной системе составим определитель   и вычислим.

 

 2. Составить и вычислить следующие определители:

 .

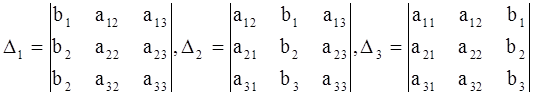3. Воспользоваться формулами Крамера.

 

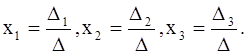
Практическое значение правила Крамера для решения системы n линейных уравнений с п неизвестными невелико, так как при его применении приходится вычислять п +1 определителей n-го порядка: D , D _{x 1} , D _{x 2} , …, D x_n. Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.

 

Примеры решения систем линейных уравнений методом Крамера

 

 

Пример 1

 

                      .

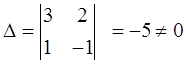
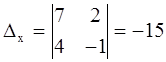
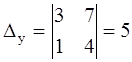
 Проверка:

                              Ответ: ( 3 ; -1 ).

 

Пример 2

                     

  

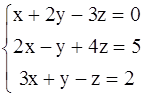
Проверка:

                   Ответ: x=0,5; y=2; z=1,5 .

 

 

           

 

Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.

       Итак, пусть дана система, содержащая m линейных уравнений с п неизвестными:

                               а₁₁х₁ + а₁₂х₂ + …+ а_{1 n} х_n = b₁;

                               а₂₁х₁ + а₂₂х₂ + …+ а_{2 n} х_n = b₂;                    

_.                                    ……………………………………

                              а_m1х₁ + а_m2х₂ + …+ а_{m n} х_n = b_m

       Метод Гаусса решения системы заключается в последовательном исключении переменных.

Схема единственного деления. Рассмотрим простейший вариант метода Гаусса, называемый схемой единственного деления.

Прямой ход состоит из n - 1 шагов исключения.

1-й шаг. Целью этого шага является исключение неизвестного x₁ из уравнений с номерами i = 2, 3, …, n. Предположим, что коэффициент a₁₁ ¹ 0. Будем называть его главным элементом 1-го шага.

Найдем величины

q_i1 = a_i1/a₁₁ (i = 2, 3, …, n),

называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, …, n -го уравнений системы первое уравнение, умноженное соответственно на q ₂₁, q₃₁, …, q_n1. Это позволит обратить в нуль коэффициенты при x₁ во всех уравнениях, кроме первого. В результате получим эквивалентную систему

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1n x_n = b₁ ,

a₂₂⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + … + a_2n⁽¹⁾x_n = b₂⁽¹⁾ ,

a₃₂⁽¹⁾x₂ + a₃₃⁽¹⁾x₃ + … + a_3n⁽¹⁾x_n = b₃⁽¹⁾ ,

. . . . . . . . . . . . . . .

a_n2⁽¹⁾x₂ + a_n3⁽¹⁾x₃ + … + a_nn⁽¹⁾x_n = b_n⁽¹⁾ .

в которой a_ij⁽¹⁾ и b_ij⁽¹⁾ вычисляются по формулам

a_ij⁽¹⁾ = a_ij − q_i1a_1j    , b_i⁽¹⁾ = b_i − q_i1b₁.

2-й шаг. Целью этого шага является исключение неизвестного x₂ из уравнений с номерами i = 3, 4, …, n. Пусть a₂₂⁽¹⁾ ≠ 0, где a₂₂⁽¹⁾ ­– коэффициент, называемый главным (или ведущим) элементом 2-го шага. Вычислим множители 2-го шага

q_i2 = a_i2⁽¹⁾ / a₂₂⁽¹⁾ (i = 3, 4, …, n)

и вычтем последовательно из третьего, четвертого, …, n -ого уравнения системы второе уравнение, умноженное соответственно на q₃₂, q₄₂, …, q_m2. В результате получим систему

       a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1n x_n = b₁ ,

                   a₂₂⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + … + a_2n⁽¹⁾ = b₂⁽¹⁾ ,

                                   a₃₃⁽²⁾x₃ + … + a_3n⁽²⁾x_n = b₃⁽²⁾ ,

. . . . . . . . . . . . . . . . . . .

                                   a_n3⁽²⁾x₃ + … + a_nn⁽²⁾x_n = b_n⁽²⁾ .

Здесь коэффициенты a_ij⁽²⁾ и b_ij⁽²⁾ вычисляются по формулам

a_ij⁽²⁾ = a_ij⁽¹⁾ – q_i2a_2j⁽¹⁾ , b_i⁽²⁾ = b_i⁽¹⁾ – q_i2b₂⁽¹⁾.

Аналогично проводятся остальные шаги. Опишем очередной k -й шаг.

k -й шаг. В предположении, что главный (ведущий) элемент k -ого шага a_kk^(k–1) отличен от нуля, вычислим множители k -го шага

q_ik = a_ik^(k–1) / a_kk^(k–1) (i = k + 1, …, n)

и вычтем последовательно из (k + 1)-го, …, n-го уравнений полученной на предыдущем шаге системы k-e уравнение, умноженное соответственно на q_k+1,k, q_k+2,k, …, q_nk.

После (n - 1)-го шага исключения получим систему уравнений

       a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n =   b₁   ,

                   a₂₂⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + … + a_2n⁽¹⁾x_n = b₂⁽¹⁾ ,

                                   a₃₃⁽²⁾x₃ + … + a_3n⁽²⁾x_n = b₃⁽²⁾ ,

       . . . . . . . . . . . . . . . . . . . .

                                                           a_nn^(n–1)x_n = b_n^(n–1) .

матрица A^(n-1) которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.

Алгоритм для решения системы линейных уравнений методом Гаусса

Выражаем первое неизвестное из первого уравнения и подставляем его в остальные уравнения.

1. Получаем новую систему, в которой число уравнений и неизвестных на 1 меньше.
2. С новой системой поступаем таким же образом и так продолжаем до тех пор, пока не останется одно линейное уравнение, которое легко решается.
3. Когда получено значение последнего неизвестного x_n, подставляем его в уравнение, которое позволяет найти x_{n – 1} по x_n.
4. По найденным x_{n – 1} и x_n находим x_{n – 2} и таким образом находим последовательно все неизвестные.

Для систем нелинейных уравнений этот метод не всегда применим уже в силу того, что из уравнений системы совсем не обязательно можно будет выразить одну неизвестную через остальные.

---

Дата добавления: 2021-05-18; просмотров: 93; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!