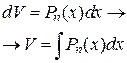Содержание практического занятия:
А. Ответить на вопросы:
1) В чем заключается правило Лопиталя. В каких случаях оно употребляется?
2) Как использовать правило Лопиталя для раскрытия неопределенностей различных типов?
3) Приведите примеры использования правила Лопиталя для раскрытия неопределенностей различных типов.
Б. Выполнить задания:
Задание 1 . Найти пределы, используя правило Лопиталя.
1)  2)
2)  3)
3) 
Задание 2 . Найти пределы, используя правило Лопиталя.
1)  2)
2) 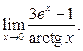 3)
3) 
Тема: Неопределенный интеграл. Таблица интегралов.
Цель: сформировать умение вычислять неопределенные интегралы, знать таблицу основных интегралов.
Теоретические сведения к практическому занятию
Функция  , определенная на интервале
, определенная на интервале  , называется первообразной для функции
, называется первообразной для функции 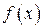 , определенной на том же интервале
, определенной на том же интервале  , если
, если 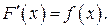
Если  — первообразная для функции
— первообразная для функции 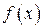 , то любая другая первообразная
, то любая другая первообразная 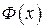 для функции
для функции 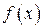 отличается от
отличается от  на некоторое постоянное слагаемое, т. е.
на некоторое постоянное слагаемое, т. е.  где
где 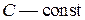 .
.
Неопределенным интегралом от функции 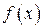 называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:
называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл: 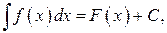 где
где 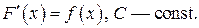
Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию:

Для проверки правильности выполненного интегрирования необходимо продифференцировать результат интегрирования и сравнить полученную функцию с подынтегральной.
Свойства неопределенного интеграла:
1. 
2. 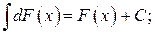
3. 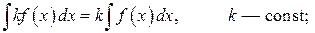
4. 
Таблица основных интегралов
1.  2.
2. 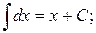
3. 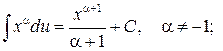

4.  5.
5. 
6. 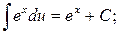 7.
7. 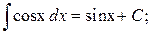
8.  9.
9. 
10.  11.
11. 
12.  12а.
12а. 
13.  14.
14. 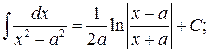
15.  16.
16. 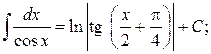
17.  18.
18. 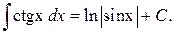
Каждая из приведенных в таблице формул справедлива на промежутке, не содержащем точек разрыва подынтегральной функции. Вычисление интегралов с использованием таблицы и основных свойств называют непосредственным интегрированием.
Пример 1. Пользуясь таблицей основных интегралов и свойствами неопределенного интеграла, найти интегралы (результат интегрирования проверить дифференцированием):


Решение.
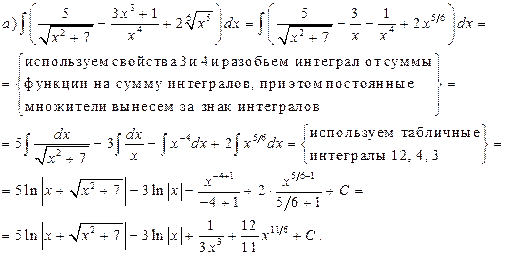 Проверка:
Проверка:
19


Проверка:
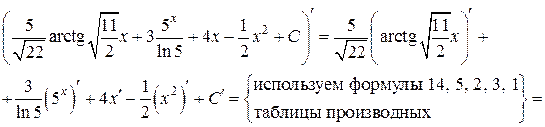

Самостоятельная работа:
Задание 1. Выполните доклад на тему «История возникновения и развития интегралов»
Задание 2. Вычислить интегралы.
1) 
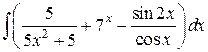
2) 

3) 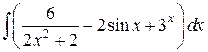
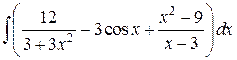
4) 
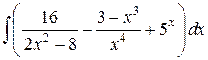
Содержание практического занятия:
А. Ответить на вопросы:
1) Дайте определение первообразной функции.
2) Дайте определение неопределенного интеграла функции.
3) Сформулируйте основные свойства неопределенного интеграла. Приведите примеры.
4) Как называется операция нахождения первообразной функции?
5) Приведите таблицу основных интегралов функций.
Б. Выполнить задания:
Задание 1. Вычислить интегралы.
1) 
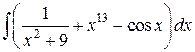
2) 

3) 

4) 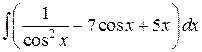

Задание 2. Вычислить интегралы.
1) 
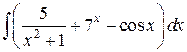
2) 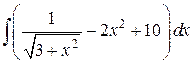

21
Тема: Методы интегрирования
Цель: сформировать умение вычислять неопределенные интегралы, используя различные методы интегрирования.
Теоретические сведения к практическому занятию:
Функция  , определенная на интервале
, определенная на интервале  , называется первообразной для функции
, называется первообразной для функции 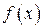 , определенной на том же интервале
, определенной на том же интервале  , если
, если 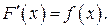
Неопределенным интегралом от функции 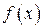 называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:
называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл: 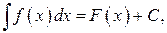 где
где 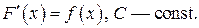
Вычисление интегралов с использованием таблицы интегралов и основных свойств называют непосредственным интегрированием.
Метод замены переменной
Теорема 1. Пусть 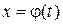 монотонная, непрерывно дифференцируемая функция, тогда
монотонная, непрерывно дифференцируемая функция, тогда
 (1)
(1)
При этом, если  то
то  где
где 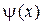 — функция, обратная
— функция, обратная 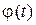 .
.
Формула (1) называется формулой замены переменной в неопределенном интеграле.
Алгоритм замены переменной:
1) Связать старую переменную интегрирования 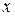 с новой переменной
с новой переменной 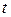 с помощью замены
с помощью замены 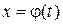 .
.
2) Найти связь между дифференциалами  .
.
3) Перейти под знаком интеграла к новой переменной.
4) Проинтегрировать и в полученной первообразной вернуться к старой переменной, подставив 
Пример 1. Проинтегрировать подходящей заменой переменной.

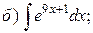
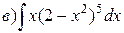
Решение:


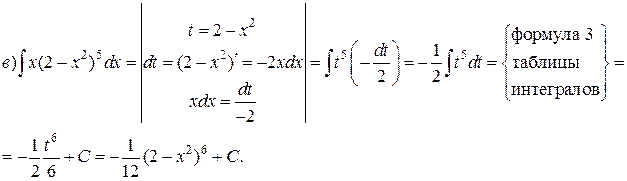
Интегрирование по частям.
Некоторые виды интегралов, вычисляемых по частям
Если производные функций 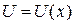 и
и 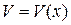 непрерывны, то справедлива формула:
непрерывны, то справедлива формула:

 (3)
(3)
называемая формулой интегрирования по частям.
В качестве  обычно выбирают функцию, которая упрощается при дифференцировании.
обычно выбирают функцию, которая упрощается при дифференцировании.
Некоторые стандартные случаи функций, интегрируемых по частям, указаны в таблице 1. Там же дается способ выбора множителей 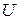 и
и  .
.
Таблица 1
| Вид интеграла | 
| 
|

| 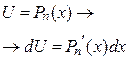
| 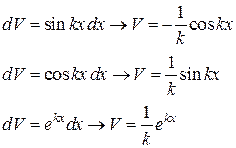
|
| Вид интеграла | 
| 
|
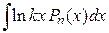
| 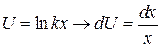
|
|
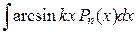
| 
| |

| 
| |

| 
| |

| 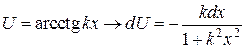
| |
|
| ||
 — многочлен от
— многочлен от 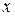 степени
степени  , т. е.
, т. е.  , где
, где  .
.
Пример 2.Проинтегрировать по частям.
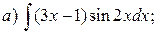

Решение.

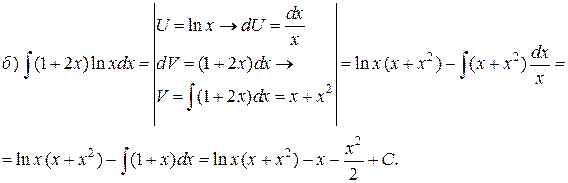
Самостоятельная работа:
Задание 1. Проинтегрировать подходящей заменой переменного.
1) 
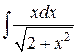

2) 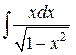
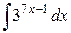
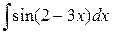
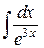
Задание 2. Проинтегрировать по частям.
1) 

2) 
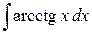
3) 

Дата добавления: 2021-04-15; просмотров: 95; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!