ДИСКРЕТНЫЕ СИСТЕМЫ.СИСТЕМЫ УПРАВЛЕНИЯ С ЭВМ

 

5.1 Понятие о дискретном управлении

Задачи дискретного управления возникают в двух случаях: процесс управления по своей сути является дискретным; для управления непрерывным процессом используется дискретное управляющее устройство, в частности ЭВМ.
Дискретные регуляторы появились еще в прошлом столетии для регулирования паровых машин "на отсечку пара". Их исследование привело к рождению теории прерывистого регулирования на основе линейных разностных уравнений.
Позднее, в связи с появлением турбин и усовершенствованием паровых машин, регуляторы на отсечку потеряли свое значение, и интерес к теории дискретного управления на некоторое время ослаб.
В 20-е годы нашего столетия он возрождается в связи с созданием вибрационных и импульсных регуляторов электрических машин. Однако в определенных условиях работы динамические свойства импульсных и непрерывных линейных САУ достаточно хорошо совпадают, поэтому существенного развития теория дискретного управления в те годы не получила.
В 30-е годы интерес к дискретным системам усилился в связи с появлением регуляторов с падающей дужкой для медленных теплоэнергетических процессов. Действие этих регуляторов в какой-то степени аналогично действию человека, импульсами управляющего смесителем горячей и холодной воды при регулировании ее температуры: наблюдение за поведением системы во время паузы облегчает принятие решения о направлении и величине последующего импульса.
В регуляторах с падающей дужкой сравнительно просто и эффективно была решена проблема управления мощными сервомоторами от маломощных сигналов термопар.
Эти и аналогичные им устройства широко применяются для управления разнообразными объектами и в настоящее время.
В 40-е и 50-е годы в связи с развитием импульсной радиосвязи, радиолокации и вычислительной техники появляются дискретные САУ, использующие ЭВМ, и начинается новый этап развития теории дискретного управления.
Функциональная схема дискретной САУ не имеет принципиальных отличий от типовой схемы, представленной на рис. 1.7.
По сути, основное отличие дискретной САУ от непрерывной состоит в элементе ППЭ (см. рис. 1.7).
В дискретной САУ этот элемент является элементом дискретного действия, замыкающим и размыкающим контур управления. Далее данный элемент именуется ДЭ - дискретный элемент.
При комбинированном управлении возможно применение ДЭ и в качестве ПЭВ (см. рис. 1.7).
Во многих случаях схему дискретной САУ посредством переноса связей и воздействий, а также других преобразований удается привести к структурной схеме, представленной на рис. 5.1, где все элементы с непрерывными характеристиками и инерционными свойствами объединены в непрерывную часть (НЧ) системы, а безынерционный элемент дискретного действия представлен звеном ДЭ.

Рис. 5.1 - Дискретная САУ

Управляемая (регулируемая) величина y(t) на выходе НЧ, задающее воздействие g(t) и их разность - ошибка регулирования x(t) = g(t)-у(t) на входе ДЭ являются непрерывными функциями времени. ДЭ, часто называемый также импульсным элементом или аналого-цифровым преобразователем (АЦП), преобразует x(t) в последовательность импульсов z(t). Процесс преобразования непрерывной функции x(t) в дискретную z(t), осуществляемый ДЭ, называется квантованием. Различают три основных вида квантования: по времени, по уровню и комбинированное, сочетающее квантование по времени и по уровню. В соответствии с тремя способами квантования дискретные системы делят на три основных типа: импульсные, релейные и релейно-импульсные, или цифровые САУ. Отметим, что чаще всего под дискретными системами понимают только системы, в которых осуществляется квантование по времени, т.е. импульсные и цифровые, а релейные системы выделяют в особый тип САУ.
Рассмотрим способы квантования, наиболее распространенные в дискретных системах (рис. 5.2).

Рис. 5.2 - Квантование

На рис. 5.2, а квантование осуществляется по времени: значения непрерывной функции x(t) выделяются в дискретные моменты времени t_n(n = 0, ±1, ±2,...), называемые также моментами квантования. Квантование - это линейная операция. Моменты квантования часто отделены друг от друга равными промежутками времени, т.е. t_n = n•T , где T_n- период квантования (период чередования или повторения импульсов). Совокупность ординат х[n]=х(nT_n), n=0,1,2,..., называется решетчатой функцией, соответствующей непрерывной функции x(t). Решетчатая функция имеет дискретный аргумент, но ее ординаты могут принимать любые значения непрерывной функции. На рис. 5.2, б, в, г показано квантование функции по уровню. Выходная величина z(t) может принимать конечное множество значений, зависящих от достижения функцией x(t) некоторых пороговых значений. На рис.5.2,б пороговое значение только одно и равно величине срабатывания х_ср, поэтому при x(t) ≥ х_ср
z(t)= a = const; при x(t) < x_ср z(t) = 0.
Эта система относится к числу двухпозиционных релейных систем, реализующих принцип "включено - выключено". НА рис. 5.2, в представлена характеристика трехпозиционной релейной системы, имеющей два пороговых значения (+х₁, х₁) и зону нечувствительности между ними. На рис. 5.2, г показано квантование в многопозиционной релейной системе. Выходная величина ДЭ изменяется всякий раз, когда функция x(t) переходит через один из уровней квантования. На рис. 5.2, д показа но одновременное квантование по уровню и по времени. Значения функции фиксируются в равноотстоящие дискретные моменты времени пТп, при этом значения выходных величин округляются, например, до большего ближайшего уровня или до ближайшего меньшего уровня. Из трех основных типов дискретных САУ релейные системы являются существенно нелинейными, элементы теории которых были рассмотрены в разделе 4. В настоящем разделе изучим подробнее САУ, в которых осуществляется квантование по времени, т.е. импульсные и цифровые САУ. Для них главным в механизме квантования является квантование по времени. На рис. 5.2, а, д приведены примеры периодического квантования. Существуют и более сложные способы квантования. Например, в разных контурах управления могут использоваться разные периоды квантования. Такое квантование называется многочастотным и может рассматриваться как суперпозиция нескольких схем периодического квантования. Периодическое квантование изучено достаточно хорошо. В последние годы роль многочастотного квантования усиливается в связи с развитием многопроцессорных систем, а также в связи с техническими преимуществами использования разных частот квантования для различных переменных.
Рассмотрим особенности квантования в импульсных САУ. Прежде всего отметим, что для данного типа САУ ДЭ принято называть импульсным элементом (ИЭ). Квантование, осуществляемое ИЭ в виде преобразования непрерывного сигнала x(t) в последовательность импульсов z(t), называется импульсной модуляцией. Она заключается в изменении какого-либо параметра импульсов в зависимости от входного сигнала: амплитуды, длительности или момента начала действия импульса (обычно форма импульсов сохраняется при модуляции неизменной). В соответствии с этим различают три вида модуляции импульсов:

1) амплитудно-импульсную модуляцию (АИМ), при которой амплитуда импульсов а зависит от значения входного сигнала в момент начала действия импульса t_n (рис. 5.3), т.е. a(t_n) = k_ux(t_n)

Рис. 5.3 - Аплитудо-импульсная модуляция

 

2) широтно-импульсную модуляцию (ШИМ), при которой длительность импульса Т_u зависит от значения входного сигнала в момент начала действия импульса (рис. 5.4), т.е. T_u(t_n) = χx(t_n)

Рис. 5.4 - Широтно-импульсная модуляция

 

3) временную импульсную модуляцию (ВИМ), при которой временной сдвиг Т_с (запаздывание) импульса зависит от, значения входного сигнала в определенный момент времени (рис. 5.5), т.е. T_с(t_n) = χx(t_n).

Рис. 5.5 - Временная импульсная модуляция

При АИМ и ШИМ модулирующий сигнал изменяет площадь (интенсивность) импульсов.
При ВИМ площадь импульса остается постоянной. Зависимость модулируемого параметра вырабатываемых импульсов от соответствующих дискретных значений входной переменной называется характеристикой ИЭ.
ИЭ с линейной характеристикой является линейным, а ИЭ с нелинейной характеристикой - нелинейным.
Обычно ИЭ работает периодически, вырабатывая по одному импульсу за каждый период.
Период следования импульсов T_n называется периодом повторения импульсов, или тактом дискретной системы. Величина ω = 2π/Т_п представляет собой частоту повторения импульсов.
Отношение длительности (средней в случае ШИМ) одного импульса к периоду повторения импульсов γ = Т_и/Т_п представляет собой относительную длительность импульсов. Величину 1 - γ принято называть скважностью ИЭ. Форма импульсов на выходе ИЭ может быть разной: прямоугольной, треугольной, совпадающей по форме с кривой x(t) во время импульсов и т.п. Для удобства исследования часто заменяют ИЭ, генерирующий импульсы сложной формы, последовательным соединением идеального ИЭ, генерирующего импульсы вида δ-функций, и формирователя, преобразующего δ-функцию в импульсы заданной формы.
Если на входе формирователя действует δ-функция k•δ(t),а z(t) - уравнение импульса на его выходе, то передается точная функция формирователя
При линейной непрерывной части системы, имеющей передаточную функцию W_л(p), формирователь можно отнести к НЧ и считать, что НЧ имеет передаточную функцию
W_н(p) = W_ф(p)W_л(p).
Функциональная схема импульсной САУ по-прежнему будет иметь вид, представленный на рис. 5.1.
Перейдем к рассмотрению особенностей цифровых САУ.
При их реализации широко используются ЭВМ в роли управляющего устройства (рис. 5.6).

Рис. 5.6 - Цифровая САУ

Непрерывный выходной сигнал x(y) объекта управления преобразуется в цифровую форму АЦП. В зависимости от желания исследователя АЦП может рассматриваться как отдельное устройство или как составная часть ЭВМ.
Преобразование осуществляется в моменты квантования t_n и заключается в квантовании непрерывной величины по времени, по уровню и представлении полученных дискретных значений в виде чисел, т.е. в цифровом коде. В зависимости от принципа действия АЦП это преобразование может осуществляться либо путем последовательного выполнения перечисленных выше действий, либо сразу в виде одной операции. Описываемое преобразование называется кодоимпульсной модуляцией. Поэтому цифровые системы иногда именуют коде импульсными системами. Соответственно АЦ - преобразование называют кодированием, а обратное ЦА - преобразование - декодированием.
В отличие от импульсной модуляции, применяемой в импульсных САУ, в данном случае каждое значение преобразуемой входной величины представляется не одним импульсом модулируемый параметр которого (амплитуда - высота, длительность - ширина, момент начала действия импульса - фаза пропорционален входной величине, а серией импульсов. Каждое численное значение входной величины представляется определенной комбинацией этих импульсов, соответствующей дискретным значениям модулируемого параметра.
Существуют различные цифровые коды. Простейший из них - единичный код: каждое значение дискретной величины представляется числом импульсов, равным числовому значении величины. В случае десятичного кода дискретная величина выражается в виде десятичного числа и представляется серией импульсов, количество которых равно количеству разрядов этого числа. Каждый импульс несет информацию о цифре определенного разряда. Для этого модулируемый параметр импульса принимает одно из десяти дискретных значений.
Наибольшее распространение получил двоичный код: каждый разряд двоичного числа принимает одно из двух значение (0 или 1) и соответственно модулируемому параметру каждого импульса, представляющего значение одного из разрядов, тоже придается одно из двух крайних значений. Знак величины передается с помощью отдельного импульса с двумя возможными значениями модулируемого параметра.
В самом простом случае при учете только знака входной величины получается двухпозиционная релейная система с квантованием еще и по времени.
Преобразованный сигнал {y(t_n)} интерпретируется ЭВМ как последовательность чисел. ЭВМ обрабатывает эту последовательность по некоторому алгоритму и выдает новую последовательность чисел {y(t_n)} - которая преобразуется в непрерывный сигнал u(t) цифроаналоговым преобразователем (ЦАП). Заметим что САУ между ЦА- и АЦ- преобразователями разомкнута.
Таймер реального времени синхронизирует работу ЭВМ. Каждая операция в ЭВМ занимает определенное время, но на выходе ЦАП должен быть непрерывный по времени сигнал. ЦАП преобразует цифровые величины {u(t_n)} (см.рис.5.6) в ступенчатую функцию u(t)=u(nt_n), которая изменяется скачком в моменты t_n=nT_n, а в промежутке между этими моментами сохраняется неизменной или изменяется по определенному экстраполяционному закону (линейно, квадратично и т.д.).
Следовательно, управляющий сигнал u(nT_n) подобен квантованному по уровню сигналу с АИМ при γ = 1. Однако, если импульсные САУ могут быть как линейными, так и нелинейными, то наличие в цифровых САУ квантования по уровню делает их принципиально нелинейными, как и релейные САУ.
ЭВМ по-разному могут быть использованы для управления объектом или процессом, начиная от периодических вычислений вне контура управления и заканчивая работой в замкнутом контуре системы управления в реальном масштабе времени.
В настоящее время ЭВМ широко применяются для управления разнообразными объектами и процессами: технологическими процессами и производством, организационными и организационно-технологическими комплексами.
Условно можно выделить четыре этапа внедрения ЭВМ в системы управления: начальный этап; этап прямого цифрового управления; этап миникомпьютерной техники; этап микропроцессорной техники.
На 4-м этапе стоимость микрокомпьютеров резко снизилась и появилась возможность модульного наращивания их вычислительной мощности. Следовательно, становится реальным дискретное (цифровое) управление любым объектом независимо от его масштабов.
Развитие вычислительной техники стимулирует развитие теории управления и практическую реализацию все более сложных алгоритмов дискретного управления.

5.2 Математическое описание дискретных систем

Дискретная система может быть описана как с помощью внешних, так и внутренних математических моделей. Внешние модели являются моделями типа "вход - выход" и выражают зависимость только между выходом и входом системы, а внутренние модели, в частности модели пространства состояний описывают все внутренние связи между переменными системы.
Рассмотрим вначале дискретные (импульсные) линейные САУ и покажем, что для их описания могут использоваться дискретные аналоги временных (переходных), передаточных и частотных функций, рассмотренные в подразделе 2.1. Уточнение в скобках типа дискретной САУ означает, что главным в механизме квантования является квантование по времени, а особенности преобразования полученных дискретных значений не рассматриваются.

5.2.1 Характеристики дискретных (импульсных) линейных САУ

Рассмотрим случай, когда НЧ САУ является нестационарной линейной системой. Обозначим через w_k(t) реакцию дискретной линейной системы на кратковременное входное возмущение, равное единице и действующее только в течение времени действия k -го импульса. Тогда ее реакция на кратковременное возмущение, равное x(t_k) и действующее только в течение времени действия k-го импульса, будет на основании принципа суперпозиции равна w_k(f)x(t_k).
Реакция дискретной линейной системы на всю последовательность импульсов, модулированных входным возмущением x(t) , в силу принципа суперпозиции определится формулой
(5.1)
Это основная формула, определяющая зависимость выходной переменной дискретной нестационарной линейной САУ от входного сигнала.
Функции w_k(t) определяют долю, или удельный вес, значений входной переменной, действующих в различные моменты времени t_k, в формировании выходной переменной системы в любой момент времени t. Поэтому функции w_k(t) называются весовыми коэффициентами дискретной линейной системы.
Весовые коэффициенты w_k(t) полностью характеризуют дискретную линейную систему, так как, зная эти функции, можно вычислить реакцию дискретной линейной системы на любое входное возмущение x(t).
Для физически возможной дискретной линейной системы, находящейся в покое до момента t₀ формула (5.1) примет следующий вид:
(5.2)
где неравенство под знаком суммы означает, что суммирование распространяется только на моменты действия импульсов t_kє[t₀, t].
Если положить в (5.1) x(t)= δ(t - τ), то получим формулу для весовой (импульсной переходной) функции w(t,τ) дискретной линейной системы:
(5.3)
Следовательно, весовая функция любой дискретной линейной системы представляет собой линейную комбинацию δ - функций, и наоборот.
Конкретизируем описание дискретной линейной системы: пусть НЧ представляет собой непрерывную линейную систему с весовой функцией w₁(t,τ) (рис. 5.7), а ИЭ осуществляет АИМ.

Рис. 5.7 - Импульсная САУ

Обозначим функцию, описывающую форму импульсов, вырабатываемых ИЭ, через η(t) (рис. 5.8). Тогда выходной АИМ - сигнал линейного ИЭ выразится формулой

Эта функция является входной переменной непрерывной линейной системы с весовой функцией w₁(t,τ), следовательно,

Рис. 5.8 - Выходной сигнал ИЭ

Поскольку только для , то

Из сравнения этой формулы с (5.1) следует, что

Вводя переменную получим
(5.4)
Отсюда следует, что весовые коэффициенты последовательного соединения ИЭ и непрерывной линейной системы зависят от формы импульсов, вырабатываемых ИЭ, и весовой функции НЧ системы. Из (5.4) видно, что практически для любой физически возможной дискретной линейной системы начальные значения весовых коэффициентов w_k(t_k) = 0, поскольку при t = t_k подинтегральная функция тождественно равна нулю в интервале интегрирования (так как по определению w_k(t) = 0, при t < t_k) Для физически возможной дискретной системы w_k(t_k) могут быть отличны от нуля в теоретическом случае идеализированного ИЭ, вырабатывающего без запаздывания импульсы:
если при этом
Пример 5.1. Найти весовые коэффициенты дискретной линейной системы, представляющей собой последовательное соединение ИЭ, вырабатывающего единичные прямоугольные импульсы длительностью Т_u, и апериодического звена.
Подставляя в (5.4) выражение весовой функции апериодического звена и принимая во внимание, что при , получим
(5.5)
На этом примере легко проверить, что w_k(t_k) =0.
Рассмотрим дискретную систему с ШИМ, при этом будем для простоты считать, что ИЭ (см. рис. 5.7) вырабатывает прямоугольные импульсы постоянной величины а, длительность которых пропорциональна значениям входного сигнала в соответствующие моменты времени. Тогда на вход НЧ поступают сигналы z(t) = a для моментов времени tє[t_k,t_k + χx(t_k)] и z=0 вне этого интервала. Согласно (2.10), получим
(5.6)
Очевидно, что система, описываемая формулой (5.6), нелинейна. Однако при малой длительности импульсов ее можно приближенно рассматривать как линейную, так как в этом случае (5.6) перепишется в виде

Отсюда следует, что при ШИМ с кратковременными прямоугольными импульсами последовательное соединение ИЭ и непрерывной системы с весовой функцией w₁(t,τ) является линейной дискретной системой, весовые коэффициенты которой определяются соотношением
. (5.7)
Величина аχ определяет интенсивность импульсов.
Аналогичные выкладки позволяют сделать вывод о том, что при ВИМ с импульсами произвольной формы последовательное соединение ИЭ и непрерывной линейной системы является линейной дискретной системой лишь при условии, что максимальный возможный временной сдвиг импульса настолько мал, что весовую функцию НЧ системы w₁(t,τ) можно приблизительно считать линейной функцией τ в диапазоне возможных значений временного сдвига.
Во многих случаях выходная переменная дискретной линейной системы интересует нас лишь в определенные моменты времени t'_l(l=0,±1,±2,...), или система выдает выходную переменную только в определенные моменты времени t'_l. Полагая в (5.1) t = t'_l, получим
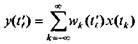(5.8)
Обозначая для краткости записи формулы (5.8) x_k=x(t_k), , получим
(5.9)
Для случая, когда последовательность моментов фиксации выходной системы совпадает с последовательностью моментов действия импульсов t'_l = t_l, формула (5.2) при t = t_l определяет следующее выражение для выходной переменной физически возможной дискретной линейной системы:
(5.10)
Формулы вида (5.10) описывают, в частности, работу ЭВМ, когда результаты вычислений линейно зависят от исходных данных В этом случае исходные данные для линейной программы вычислений на ЭВМ, вводимые на каждом шаге вычислений, являются входными сигналами, а результаты вычислений на ЭВМ - выходными переменными.
Весовые коэффициенты ω_lk определяют линейную программу вычислений. Т.е. формула (5.10) на простейшем примере показывает, что динамические характеристики ЭВМ полностью определяются программой вычислений, т.е. решаемой задачей.
Перейдем к рассмотрению частного случая, когда НЧ САУ является стационарной линейной системой.
Известно, что стационарной называется такая система, реакция которой на любой данный тип возмущения зависит только от интервала времени между данным моментом времени и моментом начала действия возмущения.
С помощью рис. 5.2, а нетрудно убедиться в том, что дискретная система не может быть стационарной в смысле данного определения. Легко проверить, что при сдвиге входного возмущения во времени на величину, не равную целому числу периодов повторения (пунктирная кривая 2), значения входного возмущения x(t), действующего на систему, изменяются и вследствие этого выходной сигнал системы не только сдвигается во времени, но и изменяет свою форму.
Но если пренебречь интервалами времени, меньшими периода повторяемости импульсов Т, то можно определить стационарную и нестационарную дискретную систему.
Дискретную систему назовем стационарной, если при сдвиге во времени входного возмущения без изменения его формы на интервал времени, кратный периоду повторения импульсов, выходная переменная сдвигается во времени на такой же интервал без изменения своей формы, т.е. дискретная система может быть стационарной только тогда, когда действующие на систему входные возмущения следуют друг за другом через равные про, межутки времени. По определению весовой коэффициент w_k(t) линейной дискретной системы есть ее реакция на кратковременное возмущение (т.е. его длительность меньше Т), равное единице в момент времени t_k = kT_n.
Если система стационарна, то при сдвиге кратковременного единичного возмущения во времени на интервал iT_n ее реакция сдвинется во времени на тот же интервал iT_n, не изменяя формы, т.е. будет равна w_k(t-iT_n) .
С другой стороны, реакция системы на единичное возмущение, действующее в момент t_k+i=(k + i)T , равна ее весовому коэффициенту w_k+i(t).
Следовательно, для стационарной дискретной линейной системы при любых i и k справедливо равенство
w_k+i = w_k(t-iT_n).
Полагая k = 0, получим при любом i
w_i(t) = w₀(t-iT_n) (i = 0,±1,±2,...), (5.11)
т.е. весовые коэффициенты стационарной дискретной линейной системы представляют собой одну и ту же функцию, сдвинутую во времени на интервалы, кратные периоду повторения
импульсов.
В частности, для последовательного соединения ИЭ, вырабатывающего последовательность равноотстоящих импульсов, и стационарной непрерывной линейной системы с весовой функцией w(t-τ) из формулы (5.4) получим
(5.12)
Полагая в (5.12) t = t_l = lТ_n, получим
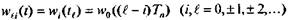, (5.13)
т.е. для стационарной дискретной линейной системы весовые коэффициенты w_li зависят только от разности индексов.
Обозначая разность индексов m, т.е. l - i = m, введем для весовых коэффициентов обозначение w_m. Для физически возможных стационарных дискретных линейных систем w(t) = 0 при t < 0, следовательно, w_m = 0 при m < 0. На основании изложенного выше для нестационарных реальных дискретных линейных систем и w₀ = 0.
Итак, весовые коэффициенты w_m последовательного соединения ИЭ и непрерывной стационарной линейной системы определяются формулой
. (5.14)
Формула (5.9) для стационарной дискретной линейной системы принимает вид
.(5.15)

5.2.2 Передаточная функция стационарной дискретной импульсной линейной системы с дискретным выходом

Рассмотрим действие на стационарную дискретную линейную систему показательного возмущения х = e^pt. В этом случае 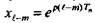, и из формулы (5.15) следует

т.е. реакция стационарной дискретной линейной системы на показательное возмущение e^pt в момент t = lT равна значению этого же возмущения в тот же момент, умноженному на функцию
(5.16)
зависящую только от комплексного параметра р. Функция W(p) является передаточной функцией стационарной дискретной линейной системы. Полагая в (5.16) р = iw, получим
(5.17)
Выражение (5.17) определяет частотную характеристику стационарной дискретной линейной системы в виде ряда Фурье. Коэффициентами этого ряда являются весовые коэффициенты системы.
Используя известную формулу для коэффициентов ряда Фурье, выразим весовые коэффициенты стационарной дискретной линейной системы через ее частотную характеристику
(5.18)
Для физически возможной стационарной дискретной линейной системы получим
(5.19)
Из формул (5.16) и (5.19) следует, что передаточные функции стационарных дискретных линейных систем являются функциями величины z = .
Обозначим через Ф(z) передаточную функцию физически возможной стационарной дискретной линейной системы, рассматриваемую как функцию параметра z, тогда
(5.20)
Справедливы тождества
W(р)≡ Ф( ); Ф(z) ≡ W((1/T_n)lnz). (5.21)
Формула (5.19) может быть получена из общей формулы (2.31), если заменить в ней функцию w(τ) линейной комбинацией δ-функций:

Это соотношение следует из (5.3). Следовательно, и для стационарной дискретной линейной системы передаточная функция является преобразованием Лапласа ее весовой (импульсной переходной) функции, которое в данном случае называется дискретным преобразованием Лапласа числовой последовательности
{w_m = {w(mT_n)} = {w[(l - i)T_n} = {w_i(t_l)} .
Функция (5.20) называется z-преобразованием последовательности величин {w_m}, а функция (5.19) является частным случаем z-преобразования.
Подобно тому как для анализа непрерывных линейных САУ удобно использовать преобразования Лапласа, для импульсных систем оказывается полезном z-преобразование и его частные случаи - дискретное преобразование Лапласа и дискретный аналог преобразования Фурье (см.(5.17)). Для выполнения этих преобразований используются теоремы и таблицы, представляющие собой дискретные аналоги табл.3.1.
Некоторые свойства z-преобразования приведены в табл.5.1.
Пример 5.2. Найти передаточную функцию замкнутой дискретной системы (рис.5.9), ИЭ которой вырабатывает прямоугольные импульсы длительностью Т_u с периодом повторения Т.

Рис. 5.9 - Пример дискретнй САУ

Найдем передаточную функцию разомкнутой системы. Подставляя в (5.20) выражения (5.5) для весовых коэффициентов разомкнутой импульсной системы, получим
(5.22)
Подставляя (5.22) в (2.58), определим передаточную функцию замкнутой системы

5.2.3 Передаточная функция стационарной дискретной импульсной линейной системы с непрерывным выходом

Наличие в импульсной системе инерционной НЧ приводит к тому, что на ее выходе процесс будет уже не дискретным, а непрерывным. Для определения значений выходных переменных в такой системе в промежутке между импульсами удобно использовать формулу t=n_n+εT_n (0≤ε<1).

 

Таблица 5.1 - Некоторые свойства z-преобразования

Подставляя это выражение в формулу (5.1) и вводя обозначения
y(nT_n+εT_n)=y_n(ε), (5.23)
w_k(nT_n+εT_n)=w₀((n-k)T_n+εT_n)=w_n-k(ε) (5.24)
получим для физически возможной стационарной дискретной линейной системы

называется передаточной функцией стационарной дискретной линейной системы с непрерывным выходом.
При p = iω формула (5.25) определяет частотную характеристику стационарной дискретной линейной системы с непрерывным выходом. Наличие в аргументе этой функции ε отражает тот факт, что дискретная система может быть стационарной в полном смысле, т.е. по отношению к любым сдвигам во времени.
На основании (5.24) w_m(0)=w₀(тT_n)=w_m, поэтому при ε = 0 (5.25) совпадает с (5.19), т.е.
W(p,0) ≡ W(p). (5.26)
Рассматривая (5.25) как функцию параметра z = , перепишем формулу (5.25) в виде
(5.27)
Функция (5.27) называется модифицированным z-преобразованием последовательности величин (5.24), а по аналогии (5.25) - модифицированным дискретным преобразованием Лапласа.

5.2.4 Описание дискретных систем разностными уравнениями

Рассматривая входную и выходную переменные дискретной системы только в определенные моменты времени t_n=nT_n (n=0,±1,±2,...), мы не имеем возможности давать времени бесконечно близкие значения и совершать предельные переходы, неограниченно сближая эти значения. Поэтому становится неудобным характеризовать скорость изменения функции ее производной. В этой связи, рассматривая поведение дискретных систем лишь в определенные равноотстоящие моменты времени, вместо производных используют конечные разности функций, а вместо дифференциальных уравнений - разностные уравнения.
Выражение
∆y[n] = ∆y(nT_n) =y((n+1)T_n) - y(nT_n) = y[n+1] - y[n] (5.28)
называется первой конечной разностью или конечной разностью первого порядка функции y(t)=(nТ_n) в точке t = nТ.
Аналогично определяются разности высших порядков. Так, ∆²у[n] = ∆(∆y[n]). Дважды применяя формулу (5.28), получим
∆²y[n] = {y[n+2] - y[n+1]} - {y[n+1] - y[n]} = y[n+2] - 2y[n+1] + y[n]. (5.29)
Заметим, что в (5.29) и далее используются введенные в (5.28) обозначения
y[n] = y(nT_n) (n=0,±1,±2,...), (5.30)
∆у[n]=у((n+1)Т_n)-y(nТ_n) (n=0,±1,±2,...). (5.31)
Если определена конечная разность (k - 1)-го порядка ∆^k-1y[n], то конечная разность k-го порядка есть ∆(∆^k-1y[n]). Методом полной математической индукции можно доказать формулу
(5.32)
где

Формула (5.32) выражает конечную разность k-го порядка через значения функции y(t) = у(nТ_n) = у[п] в точках nТ_n, (n+1)T_n, …, (n+k)T. Можно получить также формулу, в которой y[n+k] = y((n+k)T_n) выражается через конечные разности этой функции в точке nТ_n. Для этого положим по определению ∆⁰y[n] = y[n]. Тогда y[n+1] = y[n] + ∆y[n] = ∆⁰y[n] + ∆⁰y[n]. Методом полной математической индукции легко доказывается формула

где - определенные выше биномиальные коэффициенты.
Соотношение, связывающее значения неизвестной функции у[n] и разностей различных порядков ∆y[n], ∆²y[n], ..., называется уравнением в конечных разностях или разностным уравнением. Если это соотношение линейно, то оно представляет собой линейное разностное уравнение.
Разностное уравнение может содержать или значения неизвестной функции и ее разностей различных порядков при одном и том же значении аргумента t=пТ, или значения неизвестной функции при различных равноотстоящих значениях аргумента. При помощи формул (5.32) и (5.33) можно преобразовать разностное уравнение из одной формы в другую. Разностное уравнение, содержащее разности неизвестной функции до k-го порядка или значения неизвестной функции от у[n] до y[n+k], называется разностным уравнением k- го порядка.
На основании вышеизложенного стационарная дискретная линейная система описывается линейным разностным уравнением вида
c₀∆^ky[n] + с₁∆^k-1y[n] + ... + с_k∆⁰y[n] =
=d₀∆^mx[n]+ d₁∆^m-1x[n] + ... + d_m∆⁰x[n] (5.34)
или вида
a₀y[n+k] + a₁y[n + (k-1)] + … + a_ky[n] =
= b₀x[n+m] + b₁x[n+(m-1)] + ... + b_mx[n] (5.35)
Для стационарной системы коэффициенты а_i и c_i (i=0,1,...k), b_j и d_j (j=0,1,…m), m<k, являются постоянными величинами, а для нестационарной - функциями времени, правая часть уравнении (5.34) и (5.35) - заданная функция.
Итак, получено описание дискретной системы разностными
уравнениями, использующими прямые (упреждающие) разности (5.28).
Аналогично выводятся разностные уравнения на основе обратных (отстающих) разностей
∇y[n] = y(nT_n) - y((n-1)T_n = y[n]-y[n-1]. (5.36)
В этом случае уравнения дискретной САУ имеют вид:
c₀∇^k[n] + c₁∇^k-1y[n] + ... + c_k∇⁰y[n]=
= d₀∇^mx[n]+ d₁∇^m-1x[n] + ... + d_m∇⁰x[n], (5.37)
a₀y[n] + a₁y[n-1] + … + a_ky[n-k] =
= b₀x[n] + b₁x[n-1] + ... + b_mx[n-m]. (5.38)
При исследовании непрерывных линейных систем, описываемых линейными дифференциальными уравнениями, удобно использовать оператор дифференцирования р = d/dt. Для систем, описываемых линейными разностными уравнениями, можно построить аналогичное операционное исчисление. Для задания оператора определяется класс входных сигналов и его действие на них. В операционном исчислении принято, что все сигналы - неограниченные справа и слева последовательности {у[n]: n=...-1,0,1,…}. Оператор прямого сдвига, обозначаемый через q, обладает следующим свойством:
qy[n] = y[n+1]. (5.39)
Инверсия оператора прямого сдвига называется опера тором обратного сдвига q^-1, который обладает следующим свойством: q^-1y[n] = y[n-1]. (5.40)
На основании формулы (5.39) уравнение (5.35) можно переписать в комплексной форме
Q(q)y[n] = P(q)x[n], (5.41)
где Q(q) и P(g) - полиномы относительно оператора сдвига:

Определим передаточную функцию стационарной дискретной линейной системы, описываемой разностным уравнением (5.41). По определению передаточной функции, изложенному в подразделе 2.1, реакция такой системы на показательное возмущение
x(t) = e^pt, x[n] = (5.43)
определяется формулой
y[n] = Ф(z) . (5.44)
Подставляя (5.44) и (5.43) в (5.41), получим
Ф(z)Q(q) =P(q) . (5.45)
Согласно (5.39) имеем q = q = = .
Используя обозначение z = перепишем это выражение в виде
q = z , (5.46)
т.е. применение операции сдвига к показательной функции сводится к ее умножению на величину z. Следовательно,
q^lepnTn=z^lepnTn, (l=1,2,…). (5.47)
На основании формулы (5.47) мы можем заменить в уравнении (5.45) оператор q величиной z и получим алгебраическое уравнение для Ф(z). Сокращая это уравнение на и решая его, получим следующую формулу для передаточной функции системы, описываемой разностным уравнением (5.41):
Ф(z) = Р(z)/Q(z), (5.48)
Следовательно, передаточная функция стационарной дискретной линейной системы, поведение которой описывается разностными уравнениями, всегда является дробнорациональной функцией переменной z = .
Таким образом, передаточные функции стационарных дискретных линейных систем, описываемых разностными уравнениями, определяются так же, как и передаточные функции непрерывных стационарных линейных систем, описываемых дифференциальными уравнениями. В непрерывной системе оператор дифференцирования в дифференциальном уравнении заменяется параметром показательной функции р, а в дискретной системе оператор сдвига в разностном уравнении заменяется величиной . В обоих случаях в итоге получается алгебраическое уравнение для передаточной функции системы.
Отметим, что операторы дифференцирования и сдвига связаны тем же самым соотношением, что и величины р и z , т.е.
q = . (5.49)
В (5.49) в показателе экспоненты р = d/dt.
Нетрудно проверить, что передаточная функция Ф(z) стационарной дискретной линейной системы, представляющей собой последовательное соединение ИЭ и непрерывной стационарной линейной системы, описываемой дифференциальные уравнением F(p)y=H(p)x, в случае простых корней р₁,...,р_n полинома F(p) определяется формулой

где z_r = , (r=1,2,...,k), η(τ)-функция
определяющая форму импульсов, вырабатываемых ИЭ.
Если F(p) имеет кратные корни, то выражение (5.50)
усложняется, но по-прежнему будет дробно-рациональной функцией переменной z. Приводя дроби в (5.50) или в аналогичной формуле для случая кратных корней полинома F(p) к общему знаменателю, получим передаточную функцию в виде отношения двух полиномов (5.48), по которому можно легко написать соответствующее разностное уравнение. Следовательно, математической моделью рассматриваемого соединения ИЭ и стационарной линейной системы, описываемой дифференциальным уравнением, является некоторое разностное уравнение которое легко находится по дифференциальному уравнению HЧ системы и функции η(t), определяющей форму импульсов, вырабатываемых ИЭ.
Изложенные выше математические модели дискретных САУ характерны тем, что они являются моделями типа "вход - выход" и учитывают особенности механизма квантования по времени. Математические модели дискретных САУ в пространстве состояний рассмотрим на примере цифровых САУ, но по-прежнему без учета особенностей квантования по уровню. Исследование цифровых САУ показывает, что квантованный по уровню сигнал можно представить как неквантованный сигнал с наложенной на него ошибкой квантования, изменяющейся в пределах ±T_n/2. При достаточно малом шаге квантования оно эквивалентно источнику шума на входе приведенной НЧ САУ и может быть учтено при исследовании точности системы, а при достаточно большом шаге квантования цифровая САУ должна исследоваться как существенно нелинейная релейная САУ. При этом могут использоваться методы, изложенные в разделе 4.

5.2.5 Описание дискретных систем в пространстве состояний

Проблему описания непрерывной системы, связанной с ЭВМ АЦ - и ЦА - преобразователями, рассмотрим на примере (рис. 5,10).

Рис. 5.10 - Непрерывная система соединенная с АЦ - и ЦА преобразователями

Определим зависимость между сигналами в ЭВМ, представляющими собой рассмотренные выше (рис.5.2, д; рис. 5.6) последовательности {u(t_n)} и {y(t_n)}. Пусть непрерывная система задана уравнениями состояния вида (2.42). Обычно при цифровом управлении АЦП сохраняет уровень аналогового сигнала постоянным до тех пор, пока не потребуется новое преобразование, поэтому моменты квантования t_nможно определить как время, когда меняется управляющее воздействие. Следовательно, управляющий сигнал является дискретным процессом {u(t_n): n=…-1,0,1,...}.
Определим связь между переменными системы в моменты квантования. Если состояние системы в момент квантования t_n задано, то ее состояние в некоторый момент t можно получить, решив систему уравнений (2.42):
(5.51)
На основании (5.51) вектор состояния системы в момент квантования t_n+1 определяется следующим образом

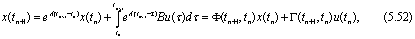
где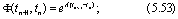

При определении второго слагаемого в (5.52) учтено, что u не изменяется в течение периода квантования. Из (5.52) следует, что вектор состояния в момент времени t_n+1 есть линейная функция от x(t_n) и u(t_n). Если АЦП и ЦАП абсолютно синхронизированы и время преобразования незначительно, то можно считать, что переменные и и у квантуются в одни и те же моменты времени. Тогда уравнения, описывающие дискретную линейную систему в пространстве состояний, примут следующий вид:

где Ф(t_n+1, t_n), Г(t_n+1, t_n) определены формулами (5.53) и (5.54).
Отметим, что уравнения (5.55) не приближенные, так как они дают точные значения переменных состояния и выходных переменных в моменты квантования, поскольку управляющие воздействие постоянно в период квантования. Поэтому уравнения (5.55) называют квантованием в приближении нулевого порядка системы уравнений (2.42). Систему (5.55) называют также эквивалентом системы (2.42) в приближении нулевого порядка.
Для квантования с периодом Т, t_n = nT_n, уравнения (5.55) описывают стационарную дискретную линейную систем поэтому

где
x[n] = x(nT_n); y[n] = y(nT_n); u[n] =u(nT_n). (5.58)
Система уравнений (5.56) решается на основе следующих итераций:
x[n₀+1] = Фx[n₀] + Гu[n₀],
x[n₀+2] = Фx[n₀+1] + Гu[n₀+1] = Ф²x[n₀] + ФГu[n₀] + Гu[n₀+1],
…
(5.59)
В полученном решении уравнения состояния две части: первая часть зависит от начальных условий, вторая является взвешенной суммой управляющих (входных) воздействий.
Инверсия квантования. Квантование определяет отображение непрерывных систем типа (2.42) в дискретные типа (5.56). Следующий простой пример показывает, что это отображение не всегда обратимо: не существует дифференциального уравнения первого порядка, которое после квантования приводило бы к разностному уравнению х[n+1] = -0,5x[n]+u[n], так как уравнение е^a = -0,5 не имеет действительного решения, поскольку экспоненциальная функция всегда положительна.
Следовательно, модель (5.56) более общая, чем (2.42). Однако, если матрица Ф не имеет действительных отрицательных собственных значений, то существует соответствующая непрерывная система.
Поведение системы между моментами квантования. Дискретные модели (5.55) и (5.56) позволяют определить значения переменных состояния и выходных переменных в моменты квантования {t_n}. Однако представляют интерес их значения между моментами квантования. Эти значения можно определить на основе выражения (5.51), которое можно переписать в виде
x(t) = Ф(t, t_n)x(t_n) + Г(t, t_n)u(t_n), (5.60)
где

5.2.6 Преобразование моделей дискретных систем в пространстве состояний

В пространстве состояний можно ввести новые координаты состояний и на этой основе осуществить преобразование моделей систем. Пусть S-невырожденная матрица и определят новый вектор состояния v[n] = Sx[n]. Тогда
v[n+1] = Sx[n+1] = SФх[п] + SГu[n ]=
= SФS^-1v[n] + SГu[n] = v[n] + u[n]
и y[n] =Сх[п] = CS^-1v[n] = v[п].
Следовательно, матрицы Ф, Г и С зависят от выбора координат для описания состояния системы. Интерес представляют инварианты, полученные после преобразования.
Теорема 5.1. Характеристическое уравнение D(λ) = |Ф - λE| = 0 является инвариантом, если новые состояния вводятся через невырожденную матрицу преобразования S.
Доказательство

Новые координаты состояния системы вводятся для получения более простой формы уравнений, описывающих ее поведение.
Диагональная форма. Предположим, что матрица Ф имеет различные собственные значения. Тогда существует матрица S
такая, что 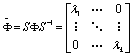, где λ₁ - собственные значения матрицы Ф. В результате преобразования получаете система разностных уравнений первого порядка:
v₁[n+l] = λ₁v₁[n] + β₁u[n],
…
v_k[n+1] = λ₁v₁[n] + β₁u[n],
y[n] = γ₁v₁[n] + ... + γ₁v₁[n].
Решение этой системы уравнений имеет вид

Если матрица Ф имеет кратные собственные значения то приводится к диагональной форме. В этом случае возможно приведение к жордановой форме. В жордановой форме преобразованная матрица имеет собственные значения на главной диагонали и несколько единиц на наддиагонали.
Наблюдаемая форма. Допустим, что характеристическое уравнения матрицы Ф имеет вид
(5.62)
и что матрица
(5.63)
невырожденна. Тогда существует такая матрица преобразования S, что преобразованная система примет вид

который называется наблюдаемой канонической формой. Примущества этой формы будут рассмотрены ниже.
Управляемая форма. Предположим, что характеристическое уравнение матрицы Ф определяется формулой (5.62), и что матрица

невырожденна. Тогда существует такое преобразование S, что преобразованная система примет вид:

который называется управляемой канонической формой. Преимущество данной формы рассматриваются ниже.
Отметим, что наблюдаемую и управляемую формы также называют присоединенными (сопряженными).

5.2.7 Преобразование уравнений состояния в модели типа "вход - выход"

Весовую (импульсную переходную) функцию дискретной системы, описываемой моделью состояния (5.56), несложно определить из формулы (5.59):

Из этого выражения следует, что импульсная переходная функция (в данном случае ее часто называют импульсной функцией) дискретной системы имеет вид

Теорема 5.2. Импульсная характеристика (5.67) инвариантна относительно линейного невырожденного преобразовав координат пространства состояний.
Доказательство.
Введем новые координаты v=Sx. Тогда импульсная характеристика преобразованной системы примет вид

Определим передаточный оператор и передаточную функцию дискретной системы, описываемой моделью (5.56).
Для получения уравнения "вход-выход" исключим и (5.56) вектор состояния х[n+1] = qх[n] = Фх[n] + Ги[n], откуда (qE - Ф)х[n] = Гu[n]. В этих соотношениях q - оператор прямого сдвига. Тогда
y[n] = Cx[n] = C(qE - Ф)^-1Гu[n]. (5.68)
Таким образом, передаточный оператор дискретной системы (5.56) имеет вид
W(q) = С(qЕ - Ф)^-1Г. (5.69)
Этот оператор также можно выразить с помощью оператор обратного сдвига W*(q^-1) = C(E - q^-1Ф)q^-1Г = W(q). Следовательно, передаточный оператор системы (5.56) является матрицей, элементы которой есть рациональные функции от q. Для одномерной системы получим
W(q) = C(qE - Ф)^-1Г = P(q)/Q(q). (5.70)
Если размерность вектора состояния равна k, а многочлены Р(q) и Q(q) не имеют общих множителей, то степень многочлена Q равна k. Из (5.64) следует, что многочлен Q также является характеристическим многочленом матрицы Ф. Это означает, что модель "вход-выход" можно записать в виде уравнений (5.34), (5.35) и (5.41).
Теорема 5.3. Передаточный оператор W(q) для модели в пространство состояний не зависит от выбора координат пространства состояний.
Доказательство.
Пусть заданы передаточный оператор (5.69) и матрица преобразования S. В новых координатах

Упомянутое выше z-преобразование можно использовать для решения уравнений состояния (5.56). Применяя z-преобразование для обеих частей уравнения (5.56)
получим
z[X(z) - x(0)] = ФХ(г) + ГU(z),
X(z) = (zE - Ф)^-1[zх(0) + ГU(z)],
Y(z) = C(zE - Ф)^-1zx(0) + C(zE - Ф)^-1ГU(z).
Следовательно, можно ввести передаточную функцию для системы (5.56) вида
W(z) = C(zE - Ф)^-1Г. (5.71)
Это соотношение идентично (5.69) с заменой q на z. Осуществляя z-преобразование, получаем последовательность y[n]. Следовательно, справедлива следующая теорема.
Теорема 5.4. Импульсная характеристика (5.67) и импульсная передаточная функция связаны z-преобразованием.

5.3 Устойчивость дискретных систем

Если выполнены условия известной теоремы Котельникова - Шеннона по неискаженной передаче непрерывного сигнала конечным числом его дискретных значений, то дискретная система сводится к непрерывной и, соответственно, ее устойчивость может исследоваться методами, изложенными в подразделах 3.2 и 4.3. Если эти условия не выполняются, то дискретная САУ должна исследоваться с учетом квантования по времени, т.е. на основе ее описания, изложенного в подразделе 5.2. При этом необходимо использовать или модели типа "вход-выход" (5.35), (5.41), (5.68) или модели пространства состояний (5.56).

5.3.1 Устойчивость дискретных линейных систем

Используем общее необходимое и достаточное условие устойчивости линейных систем (3.38) и представление весовой функции дискретной линейной системы в форме (5.3). Подставляя (5.3) в (3.38), получим общее необходимое и достаточное условие устойчивости дискретной линейной системы

Для стационарной дискретной линейной системы w_lk = w_l-k, и заменой индекса суммирования на m = l-k условие (5.72) приводится к виду

Следовательно, необходимым и достаточным условие устойчивости стационарной дискретной линейной системы является абсолютная сходимость ряда, членами которого являются ее весовые коэффициенты.
Импульсная передаточная функция стационарной дискретной линейной системы определяется формулой (5.20). Из сходимости ряда (5.73) следует, что ряд (5.20) сходится при z = 1. Но в таком случае он сходится при любом z^-1, по модулю меньшем единицы, т.е. при |z|>1. Следовательно, импульсная передаточная функция устойчивой системы конечна всюду вне единичного круга плоскости комплексной переменной z с центром начале координат.
Таким образом, для устойчивости стационарной дискретной линейной системы необходимо и достаточно, чтобы все полюсы ее импульсной передаточной функции Ф(z) лежали внутри единичного круга с центром в начале координат.
В некоторых случаях импульсную передаточную функцию Ф(z) удобно рассматривать как функцию параметра Данное соотношение называется преобразованием Мебиуса. Тогда

Обозначая импульсную передаточную функцию, рассматриваемую как функцию v, через Ω(v), получим

Преобразование Мебиуса отображает единичный круг на плоскости переменной z в левую полуплоскость переменной v. При этом окружность единичного радиуса плоскости z отображается в мнимую ось переменной v. Следовательно, для устойчивости стационарной дискретной линейной системы необходимо и достаточно, чтобы все полюсы ее передаточной функции Ω(v), рассматриваемой как функции комплексной переменной v, лежали в левой полуплоскости.
Отсюда следует, что к стационарным дискретным линейным системам применимы критерии устойчивости, рассмотренные в подразделе 3.2, но модифицированные с учетом особенностей описания дискретных систем.
Рассмотрим критерии устойчивости дискретных линейных систем с АИМ. Обозначим через = ωТ - относительную частоту, через Ф(z)=Ф( )=Ф( ) - импульсную передаточную функцию системы. Особенность дискретной передаточной функции Ф( ) состоит в том, что она является периодической функцией мнимой части с периодом 2π, так как
Физически периодичность частотной характеристики дискретной системы объясняется тем, что выходной сигнал ИЭ и, соответственно, воздействие на НЧ системы определяются значением входного сигнала только в дискретные моменты времени через промежуток времени Т.
Поэтому при гармоническом воздействии на ИЭ выходной сигнал системы не изменится при изменении частоты гармонического сигнала на любую величину, кратную .
В результате при снятии частотной характеристики путем неограниченного увеличения частоты сигнала на выходе ИЭ должна получиться периодическая характеристика.
Передаточная функция Ф( ) является периодически вдоль мнимой оси, поэтому при изучении ее полюсов на комплексной плоскости достаточно рассмотреть их в полосе ±π вдоль действительной оси (рис. 5.11).

Рис. 5.11 - Расположение полюсов передаточной функции устойчивой дискретной системы

В изложенной трактовке условия устойчивости дискретных систем совпадают с условиями устойчивости непрерывных систем. Для применения критерия Рауса-Гурвица по-прежнему используется знаменатель Q(z) передаточной функции системы (5.48). Рассмотрим пример для системы первого порядка Q(z) = a₀z + a₁. Подставляя сюда (5.74), получим

Соответствующее характеристическое уравнение имеет вид
(a₀ - a₁)γ + a₀+a₁=0,
и, следовательно, условия устойчивости Рауса-Гурвица, заключающиеся здесь в положительности коэффициентов характеристического уравнения, сведутся к неравенству а₀ > а₁.
Для системы второго порядка
Q(z) = a₀z²+a₁z+a₂.
Соответственно.

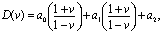
и характеристическое уравнение имеет вид
(a₀ - a₁ + a₂)λ²+2(a₀ - a₂)λ+(a₀ + a₁ + a₂)=0.
Из этого уравнения получаются следующие условия устойчивости: a₀ - a₁ + a₂ > 0; a₀ - a₀ > 0; a₀ + a₁ + a₂ > 0. Аналогично можно получить условия устойчивости для систем более высоких порядков, однако они оказываются сложнее, чем в случае непрерывных систем.
Критерий Найквиста для дискретных систем сохраняет прежнюю формулировку: условием устойчивости замкнутой системы, которая в разомкнутом состоянии устойчива, является неохват АФХ разомкнутой системы точки (-1,i0) (рис.5.12).

Рис 5.12 - Критерии устойчивости Найквиста для дискретной системы

На рисунке кривая 1 соответствует устойчивой системе, кривая 2- неустойчивой системе, а кривая 3-системе, находящейся на границе устойчивости. Разница по сравнению с непрерывным САУ заключается лишь в особенностях самих АФХ дискретных систем, которые строятся в диапазоне относительных частот от 0 до π, поэтому данные характеристики не стягиваются в начало координат, а кончаются на действительной оси, как показано на рис. 5.12. Если разомкнутая система неустойчива, и функция W( ) имеет k полюсов в правой полуполосе ±i?, то для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы конец вектора частотной характеристики W(i ) при возрастании от 0 до π повернулся вокруг точки (-1, i0) вещественной оси в положительном населении k/2 раз. Критерий устойчивости Михайлова для дискретных систем требует, чтобы годограф , представляющий собой знаменатель , начинаясь на положительной действительной полуоси комплексной плоскости , охватывал начало координат, последовательно проходя 2n квадратов, где n - порядок системы (рис. 5.13).

Рис. 5.13 - Критерий устойчивости Михайлова для дискретных систем

5.3.2 Устойчивость дискретных систем в пространстве состояний

Рассмотрим дискретное уравнение движения в пространстве состояний
x[n+1] = F[x[n],n]. (5.75)
Уравнение (5.75) обобщает (5.56) на случай нестационарной и нелинейной дискретной системы.
Пусть х*[] и х[n] - решения (5.75) при начальных условиях х*[n₀] и х[n₀] соответственно.
Приведем следующие два определения устойчивости.
1. Решение х*[n] уравнения (5.75) устойчиво, если для заданного ε > 0 существует δ(ε, n₀) такое, что для всех решений, удовлетворяющих условию
||x[n₀] - x*[n₀]|| < δ, ||x[n] - x*[n]|| < ε для всех n≥n₀.
2. Решение х*[n] уравнения (5.75) асимптотически устойчиво, если оно устойчиво и если
||x[n] - x*[n]|| → 0 при n → ∞ , при условии, что
||x[n₀] - x*[n₀]||достаточно мало.
В этих определениях и далее ||•|| обозначает норму.
Из определений следует, что устойчивость, вообще говоря, определяется для конкретного решения (движения системы), а не для системы в целом.
Рассмотрим, в частности, устойчивость стационарной дискретной линейной системы, описываемой уравнением (5.56), свободное движение которой в пространстве состояний задано
уравнением
x*[n+1] = Фх*[n], х*[0]=a* . (5.76)
Для исследования устойчивости решения уравнения (5.76) изменим начальные условия.
Тогда получим
х[n+1] = Фх[n], х[0]=a .
Разность η = х - х* удовлетворяет уравнению
η[n+1] = Фη[n], η[0] = a - a*. (5.77)
Отсюда следует, что если решение х* устойчиво, то каждое другое решение также устойчиво, т.е. для стационарных дискретных линейных систем устойчивость - это свойство системы, а не конкретного движения системы.
Согласно (5.59) система (5.77) имеет решение
η[n] = Фⁿη[0]. (5.78)
Если матрицу Ф можно привести к диагональному виду, то решение является линейной комбинацией , где (i=1,... k) - собственные значения матрицы Ф (см. (5.61)). В общем случае, когда имеются кратные собственные значения матрицы Ф и ее диагонализация невозможна, решение (5.78) представляет собой линейную комбинацию р_i[n] , где р_i[п] - многочлен, порядок которого на единицу меньше кратности собственного значения .
Для достижения асимптотической устойчивости все решения должны стремиться к нулю при n → ∞. Это возможно тогда и только тогда, когда | |<1, i=1,... n. Следовательно, справедлива следующая теорема.
Теорема 5.5. Стационарная дискретная линейная система (5.76) асимптотически устойчива тогда и только тогда, когда все собственные значения матрицы Ф лежат строго внутри единичного круга.
Из приведенных рассуждений следует, что если дискретная линейная система асимптотически устойчива, то она устойчива и по условиям (3.38), (5.72), (5.73), т.е. ограниченный вход вызывает ограниченный выход при любых начальных условиях. Таким образом, асимптотическая устойчивость самое сильное условие, поэтому далее под устойчивостью понимается асимптотическая устойчивость.
Из теоремы 5.5 следует, что непосредственно проверку устойчивости исследуемой системы можно осуществить путем вычисления собственных значений матрицы Ф. Для этого созданы пакеты прикладных программ для ЭВМ. Однако этот метод нельзя применять, если матрица имеет параметры в своих элементах.
В ряде случаев проще исследовать характеристическое значение Q(z) = 0. Характеристический многочлен Q(z) является знаменателем импульсной передаточной функции (5.20), (5.48), (5.71). Проверка устойчивости осуществляется путем исследования условий, при которых корни многочлена попадают внутрь единичного круга. При этом используются как рассмотренные выше дискретные аналоги критериев Рауса-Гурвица, Найквиста, Михайлова, так и критерии Шура, Коха и Джури, эквивалентные критерию Рауса-Гурвица, а также хорошо известный метод корневого годографа.

5.3.3 Второй метод Ляпунова

A.M. Ляпунов разработал свой метод для динамических систем, описываемых дифференциальными уравнениями (см. подраздел 4.3), но аналогичные теоремы и выводы, следующие из них, могут быть получены и для разностных уравнений.
Рассмотрим частный случай (5.69), когда движение системы в пространстве состояний описывается уравнением
x[n+1] = F[x[n]], F[0]=0. (5.79)
Функция V(x) является функцией Ляпунова для системы(5.79), если
V(x) непрерывна по x и V(0)=0 ;
V(x) положительно определена;
∆V(x) = V(F[0]) - V(x) отрицательно определена.
Теорема 5.6. Решение х[n] асимптотически устойчиво, если для системы (5.73) существует функция Ляпунова.
Кроме того, если 0 < φ(||х||) < V(x), где φ(||х||) → ∞ при ||x|| → ∞, то решение асимптотически устойчиво для любых начальных условий.
При использовании теоремы Ляпунова главная трудность состоит в построении подходящей функции Ляпунова. В общем случае это очень трудная задача, но для линейной системы (5.76) легко построить квадратичную функцию Ляпунова вида
V(x)x^TAx. (5.80)
Проверим, является ли (5.80) функцией Ляпунова. Ее приращение равно
∆V(х) = V(Фх) - V(х)= х^TФ^TАФх - х^TАх = х^T(Ф^TАФ -А)х = -х^TВх.
Для того чтобы V(x) была функцией Ляпунова, необходимо и достаточно, чтобы существовала положительно определенная матрица А, удовлетворяющая уравнению
Ф^TАФ - А = -В, (5-81)
где В - положительно определена.
Уравнение (5.81) называется уравнением Ляпунова.
Доказано, что если линейная система устойчива, то уравнение (5.81) всегда имеет решение.

5.4 Устойчивость дискретных систем

В подразделе 2.2 были сформулированы два фундаментальных свойства непрерывных динамических систем: управляемость и наблюдаемость. Первое свойство связано с возможностью перевода системы из заданного начального состояния в любое другое, а второе - с возможностью определения состояния динамической системы по наблюдаемым входам и выходам.
Рассмотрим эти свойства для дискретной системы, описываемой уравнением (5.56). Предположим, что задано ее начальное состояние х[0]. Тогда состояние системы в момент времени п (здесь п - порядок системы) определяется решением (5.59), которое в данном случае запишется в виде
x[n] = Фⁿx[0] + Ф^n-1Гu[0] + ... + Гu[n-1] = Фⁿx[0] + МU, (5.82)
где М = [ГФГ ... Ф^n-1Г]; U = [u^T[n-l] ... u^t[0]]^T.
Если М имеет ранг n, то можно найти n уравнений, решение которых определит управляющий сигнал, переводящий системy из начального состояния х[0] в желаемое конечное состояние х[n]. Такое решение неединственно, если существует более одного входного сигнала.
Определение управляемости. Система (5.56) управляема, если существует управляющая последовательность, переводящая систему из любого начального состояния в начало координат за конечное время.
Матрицу М по аналогии с непрерывными системами называют матрицей управляемости.
С управляемостью тесно связано понятие достижимости.
Определение достижимости. Система достижима, если существует управляющая последовательность, переводящая систему из любого начального состояния в произвольное состояние за конечное время.
Управляемость не означает достижимость, что следует из уравнения (5.82). Если Фⁿx[0]=0, то нулевое состояние получается при нулевом входе, но система необязательно достижима. Однако эти понятия эквивалентны, если матрица Ф обратима.
Из определения достижимости следует, что система (5.56) достижима тогда и только тогда, когда матрица М имеет ранг n.
Нетрудно показать, что матрица управляемости не зависит от выбора системы координат в пространстве состояний. Допустим, что с помощью невырожденной матрицы преобразования S введены новые координаты. В этих координатах

Если М имеет ранг n, будет того же ранга. Следовательно, достижимость системы не зависит от выбора системы координат.
Из приведенных выше определений следует, что можно найти такую управляющую последовательность, что любое состояние достигается не более чем за n шагов (тактов дискретной системы). Означает ли при этом достижимость возможность отслеживания некоторой заданной траектории в пространстве состояний? Предположим, что из произвольного известного состояния x[k] систему надо перевести в состояние x[k+1]. Из (5.82) видно, что это выполнимо только в том случае, когда матрица Г имеет ранг n, т.е. необходимо, но не достаточно иметь п входных сигналов. В частном случае одномерной системы некоторое состояние можно получить только в каждой n-й точке квантования при условии, что оно известно за n шагов до него.
Задача отслеживания заданного выхода существенно проще. Предположим, что заданная траектория есть y⁰[k]. Тогда управляющее воздействие и должно удовлетворять условию
или (5.83)
Предположим, что в системе существует временная задержка на d шагов. Тогда управление u[k] имеет причинный характер только тогда, когда требуемая траектория известна за d шагов. В этом случае управляющий сигнал вырабатывается в реальном времени. Таким образом, управляющее воздействие получают, подавая на вход обращенной системы Q(q)/P(q) требуемый выходной сигнал. Управление (5.83) имеет единственное решение, если сигнал y⁰[k] таков, что существует k₀, при котором u[k]=0 для всех k<k₀. Сигнал и ограничен, если сигнал у⁰ ограничен и обращенная система устойчива.
Для решения проблемы отыскания состояния системы по ее выходу вводится понятие ненаблюдаемых состояний: состояние х⁰ ≠ 0 ненаблюдаемо, если существует конечное k₁ ≥ n-1, такое, что y[k]=0 для 0 ≤ k ≤ k₁ при х[0] = х⁰ и u[k]=0 для 0 ≤ k ≤ k₁.
Система (5.56) наблюдаема, если существует такое конечное k, что знания входов u[0],...,u[k -1] и выходов y[0],...,y[k-1] достаточно для определения ее начального состояния.
Рассмотрим систему (5.56). Действие известного входного сигнала всегда можно определить, и поэтому общность решения не пострадает, если предположить, что u[k]=0. Пусть даны y[0],y[1],...,y[k-1]Тогда можно записать следующую систему уравнений:
у[0] = Сх[0],
y[1] = Cx[1] = СФx[0],
…
y[n-1] = СФ^n-1x[0].
Векторная запись этой системы уравнений имеет вид

(5.84)
Состояние х[0] можно определить из (5.84) тогда и только тогда, когда матрица наблюдаемости
(5.85)
имеет ранг п. Состояние х[0] ненаблюдаемо, если принадлежит нуль-пространству L. Если два состояния ненаблюдаемы, то их линейная комбинация также ненаблюдаема. Следовательно, ненаблюдаемые состояния образуют линейное подпространство. Справедливо следующее утверждение: система (5.56) наблюдаема тогда и только тогда, когда L имеет ранг n. Аналогично (см. подраздел 2.2) определялась наблюдаемость для непрерывных систем. Легко показать, что матрица наблюдаемости, так же как и матрица управляемости, не зависит от выбора системы координат. Рассмотрим четыре примера на введенные понятия.
Пример 5.3. Система

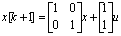
недостижима, так как

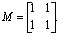
Если было бы два входа с невырожденной матрицей Г, то система достигала бы любого состояния за конечное время.
Пример 5.4. Пусть дана система

Можно ли найти такую управляющую последовательность, что х^T[2] = [-0,5 1] ? Из уравнения (5.82) следует, что х[2]=Ф²х[0]+ФГu[0]+Гu[1], или

Отсюда получаем, что 0,5u[0] + и[1] = -4 .
Следовательно, одна допустимая управляющая последовательность существует: u[0] = -2 и и[1] = -3 . Предположим теперь, что х^T[2] = [0,5 1]. Соответствующая система уравнений не имеет решения, так как система недостижима. Матрица управляемости имеет следующий вид:
Из начала координат можно достичь только тех точек в пространстве состояний, которые принадлежат подпространству, "натянутому" на вектор [1 -0,5]^T. Этот вывод следует из теоремы Гамильтона-Кэли, доказанной в теории матриц. Теорема утверждает, что если D(λ) (см. (2.43)) есть характеристическое уравнение матрицы А, тогда А удовлетворяет уравнению D(A) = 0, т.е. матрица А удовлетворяет собственному характеристическому уравнению. В силу теоремы Гамильтона-Кэли из (5.82) следует, что все состояния, достигаемые из начала координат, "натянуты" на столбец матрицы управляемости М. Это означает, что достижимые состояния принадлежат линейному подпространству, порождаемому столбцами матрицы М. В примере 5.4 достижимы и другие точки из-за влияния начального значения.
Пример 5.5. Рассмотрим систему третьего порядка (п=3)

которая записана в управляемой форме. Матрица управляемости М и обратная матрица М^-1 имеют вид:

Пример 5.5 можно обобщить до порядка п, где

Пример 5.6. Рассмотрим систему

Представим графики выходной переменной для четырех различных начальных условий (рис. 5.14).

Рис. 5.14 - Выход системы, описанной в примере 5.6:
а - [0,5 1]; б - [1,5 0,5]; в - [2,5 0]; г - [1 -0,5]

Матрица наблюдаемости имеет вид Ранг матрицы L равен 1 и наблюдаемые состояния принадлежат нуль-пространству L, т.е. [0,5 1] (рис. 5.14, а). Из рис. 5.14, б, в, г следует, что различные начальные состояния дают одинаковый выход, если они лежат на линии, параллельной линии, проходящей через состояние [0,5 1] и начало координат [0 0] (см. рис. 5.14, б, г).

5.4.1 Декомпозиция Калмана

Достижимая и ненаблюдаемая части дискретной системы - это два линейных подпространства в пространстве состояний. Они не зависят от выбора системы координат в пространстве состояний. Американский ученый Р. Калман показал, что существует такая система координат, в которой поведение дискретной системы описывается следующей блочной формой:
(5.86)
где Ф_ij, Г_i, C_i - матрицы соответствующего ранга.
Система уравнений (5.86) разлагается на четыре часта, каждая из которых соответствует достижимому и наблюдаемому, недости-жимому, но наблюдаемому, достижимому, но ненаблюдаемому, недостижимому и ненаблюдаемому состояниям. Р.Калман доказал следующую теорему.
Теорема 5.7. Линейная система может быть разложена на четыре подсистемы со следующими свойствами:
S₁ - наблюдаемая и достижимая подсистема;
S₂ - наблюдаемая, но недостижимая подсистема;
S₃ - ненаблюдаемая, но достижимая подсистема;
S₄ - ненаблюдаемая и недостижимая подсистема.
На основании этой теоремы дискретную систему представим схемой (рис. 5.15).

Рис. 5.15 - Декомпазиция Калмана

В результате несложных алгебраических преобразований импульсная передаточная функция системы может быть записана в виде Таким образом, импульсная передаточная функция системы однозначно определяется наблюдаемой и достижимой частью системы (подсистемой S₁,).

5.4.2 Потеря достижимости и наблюдаемости при квантовании

Квантование непрерывной линейной системы дает дискретную систему с матрицами, ранг которых зависит от периода квантования. Проанализируем, как влияет период квантования на достижимость и наблюдаемость дискретной системы. Для получения достижимой дискретной системы необходимо, чтобы исходная непрерывная система также была достижима, так как допустимые управляющие сигналы дискретной системы (кусочно-постоянные сигналы) есть подмножество допустимых управляющих сигналов непрерывной системы. Однако для некоторых значений периода квантования достижимость теряется.
Условия ненаблюдаемости для непрерывной системы более строгие, так как выход должен быть равен нулю на некотором интервале времени, тогда как для дискретной системы выход должен быть равен нулю только в моменты квантования. Это значит, что непрерывный выход может колебаться между моментами квантования и быть равным нулю в эти моменты. Данное явление иногда называют скрытым колебанием. Таким образом, дискретная система может быть ненаблюдаема, даже если соответствующая непрерывная - наблюдаема.
Пример 5.7. Для иллюстрации изложенного рассмотрим модель гармонического осциллятора - математический маятник (рис. 5.16). Ускорение точки подвеса является входом, а угол отклонения нити - выходом.

Рис. 5.16 - Маятник

Такая система описывается следующими нормализованными нелинейными уравнениями: где x₁ - угол отклонения; x₂ - угловая скорость. Линеаризация уравнений в окрестности точки u = х₁ = 0 дает

у = [1 0]х.
Передаточная функция для (5.87) имеет вид

и в более общем виде -

Для этой передаточной функции уравнения (5.87) перепишутся в следующем виде:

y=[1 0]х.
Система уравнений (5.88) может быть использована также для описания в первом приближении динамики подъемного крана.
Квантование (5.88) с фиксатором нулевого порядка приводит к следующей дискретной модели гармонического осциллятора:
(5.89)
y[k] = [1 0]x[k].
Определители матриц управляемости и наблюдаемости системы (5.89) имеют вид:
detM = -sinω(l - cosω),
detL = sinω.
Достижимость и наблюдаемость дискретной системы (5.89) теряется при ω = nπ, тогда как соответствующая ей непрерывная система (5.88) управляема и наблюдаема.

5.5 Графовые модели дискретной нелинейной динамической системы

Достоинства графического представления поведения систем управления в двухмерном пространстве состояний очевидны. Особенно очевидны эти преимущества при существующем уровне развития вычислительной техники и соответствующих возможностях графического представления разнообразной информации на мониторе (дисплее) ЭВМ. Однако реальные дискретные динамические системы имеют размерность пространства состояний существенно больше двухмерной. Наличие в их структуре нелинейностей создает дополнительные значительные трудности исследования таких систем. В этой связи преобразование пространства состояний дискретной нелинейной динамической системы любой конечной размерности к двухмерному, предложенное Г.А. Медведевым, представляет не только теоретический, но и практический интерес. Изложим его суть на примере дискретной нелинейной САУ (рис. 5.17).

Рис. 5.17 - Дискретная нелинейная САУ

Реальный инерционный объект управления характеризуется тем, что его выходная величина в некоторый момент времени t зависит от того, какие воздействия поступили на его вход в течение времени [t-T,t]. Величина этого временного интервала может быть и неограниченной, т.е. возможно, что Т = ∞. Из изложенного в подразделе 4.1 следует, что обычно инерционный нелинейный объект естественно представить в виде последовательного соединения трех частей (рис. 5.17): входной линейной части ОУ - линейного фильтра Л₁, выход х которого поступает на нелинейный безынерционный преобразователь Н, а его выходная величина F фильтруется линейным фильтром Л₂.
Допустим, что динамику системы характеризует следующее:
1) система работает в дискретном времени t_n=nT_n (n=0,±1,±2,...), дискретность которого определяется управляющими воздействиями (управлениями) u(nТ_n) = u[_n], где n - номер такта управления, поэтому под дискретным временем далее понимается n;
2) зависимость выхода входного фильтра Л₁ ОУ от входных воздействий имеет вид
(5.90)
где a_i - весовые коэффициенты, k - инерционность линейного звена Л₁ ОУ;
3) F - выход нелинейного звена Н, реализующего некоторую нелинейную (в нашем случае экстремальную) зависимость
F[n] = F(x[n]); (5.91)
4) выход линейного звена Л₂, который является одновременно и выходом ОУ, определяется соотношением
(5.92)
где b_j - весовые коэффициенты, m - инерционность линейного фильтра Л₂.
На основании (5.90) - (5.92) получим следующее соотношение для выхода ОУ:
= Ф(u[n], u[n -1], ..., u[n-m-k]). (5.93)
Из этого соотношения следует, что выход ОУ в момент времени и определяется набором из (m+k+1) последовательных значений управления u[n-l] (l = 0,1,...,m+k). В ТАУ принято считать, что величина m+k характеризует инерционность ОУ.
Предположим, что УУ работает по некоторому алгоритму
u[n+1] = D(u[n], u[n-1], ..., u[n-s]; у[n], y[n-1, ..., у[n-r]). (5.94)
Учитывая соотношение (5.93), алгоритм (5.94) можно представить в следующем виде
u[n+1] = D(u[n], u[n-1], ..., u[n-v]) . (5.95)
Это соотношение устанавливает связь между управлением, вырабатываемым в момент времени n+1, и предшествующими
управлениями. В (5.95) использовано обозначение
(5.96)
Величину v называют инерционностью системы. Заметим, что она отличается от (m+k) - инерционности ОУ - на число r (см. (5.94)).
Совокупность управлений u[n], u[n-1], ..., u[n-v] естественно назвать состоянием рассматриваемой системы в момент времени п, т.е. в нашем примере пространство состояний системы имеет размерность v+1. Допустим, что в системе осуществляется квантование не только по времени, но и по уровню, т.е. по значениям управлений. Единицу измерения управлений обозначим через ∆. Тогда алгоритм управления (5.94) может быть представлен в следующем виде:
(5.97) где - некоторая функция, принимающая целочисленные значения и характеризующая приращение управления на некотором такте управления п. В практике цифрового управления число возможных приращений управления, как правило, является ограниченным.
Пусть число возможных приращений управления равно w. Припишем каждому возможному приращению некоторый номер
h(0 ≤ h < w). Тогда (5.97) перепишется следующим образом:
(0 ≤ h < w). (5.98)
Отметим, что в (5.98) h = h(u[n], ..., u[n-s]; у[n], ..., у[n-r]).
В частном случае, когда w=2, возможно всего два различных приращения управления, т.е. дискретное управление является релейным, и (5.98) перепишется в следующем виде:
u[n+1] = u[n] + ƥ(1-2h), h = 0,1, (5.99)
т.е. в данном частном случае f(h) = (1-2h). Примером такого управления является управление по алгоритму с запоминанием экстремума
u[n+1] = u[n] + ∆sign[(u[n] - u[n-1])(y[n-1] - y[n])]. (5.100)
В алгоритме (5.100) функцией , принимающей целочисленные значения и определяющей приращение управления на n-м такте управления, является знаковая функция sign(...), определенная выше формулой (3.40).
Так как (v+1) - мерное пространство состояний системы дискретное, то имеется возможность перехода к двухмерному пространству состояний. Осуществим этот переход. Значения управления дискретны, поэтому они могут быть представлены в виде чисел и[п] = i•∆, где i - некоторое целое число. Далее, из (5.98) получим, что
(5.101)
Таким образом, набор управлений u[n], u[n-1], ..., u[n-v], характеризующий состояние системы, полностью определяется набором (v+1) чисел: i, h₁, h₂, ..., h_v. Это означает возможность описания состояния системы не набором конкретных значений управления, а набором (v+1) чисел, среди которых одно число i задает величину управления в данный момент времени, а остальные v чисел находятся в интервале от 0 до (w-1) и устанавливают последовательность предшествующих управлений. Иными словами, i определяет значение управления в момент времени n, а остальные числа показывают, каким образом в течение предшествующих тактов управление приближалось к этому значению. Легко установить, что существует w^v таких различных способов описания предыстории текущего управления. Пронумеруем эти способы, поставив в соответствие каждому способу число
(5.102)
Всякому из чисел l, определенных таким образом, соответствует один и только один набор чисел h₁,h₂,...h_v. Следовательно, пара чисел (i,l) полностью определяет состояние исследуемой системы.
Рассмотрим теперь возможные переходы системы из одного состояния в другое. Если в некоторый момент п система находилась в состоянии (i, l) и на следующем такте управления перешла в состояние (i', l'), то согласно (5.98) между i и i' должна существовать следующая связь: :
i '= i + f(h), 0 ≤ h < w. (5.103)
Представим число ?, определяемое (5.102), в виде
l = wα + β, 0 ≤ β < w. (5.104)
Из сравнения (5.104) с (5.102) следует, что
(5.105)
где коэффициенты h_j(1 ≤ j ≤ v) заданы соотношениями (5.101).
С учетом обозначений (5.104), (5.105) связь между l и ?l' определяется через величину α:
l' = &0945 + hw^v-1, 0 ≤ h < w. (5.106)
Таким образом, в исследуемой системе из состояния (i, wα + β) возможны переходы только в состояния
(i + f(h), α + hw^v-1), 0 ≤ h < w.
При этом из некоторого фиксированного состояния система может перейти в w различных состояний и, с другой стороны, в некоторое фиксированное состояние система может перейти из w различных состояний.
Соотношения (5.103) - (5.106) позволяют легко построить графы для изучения поведения системы в двухмерном пространстве состояний (i,l). Приведем примеры построения графов для частных случаев рассматриваемой системы. Предположим, что УУ дискретной системы реализует алгоритм (5.100). Построим графы для нескольких значений инерционности v (рис. 5.18).
1. Инерционность v=0 (рис. 5.18, а). Здесь нет необходимости в кодировании состояний двумя числами, поскольку каждое состояние системы определяется мгновенным значением управления, т.е. только одним числом i. Выше уже отмечалось, что для релейных систем w=2, f(h) = (l-2h), h = 0,1. Следовательно, из состояния i возможны два перехода: в состояние (i-1) и в состояние (i+1).
2. Инерционность v=1 (рис. 5.18, б). Состояния кодируются парами (i,l), где l=0, 1. Поэтому в (5.104) α всегда равно нулю, в (5.106) l'=h. Из состояния (i,l) возможны переходы в состояния (i+1, 0) и (i-1, 1).
3. Инерционность v=2 (рис. 5.18, в). Формулы (5.103) - (5.106) определяют, что в системе возможны следующие переходы:
- из состояния (i, 0) в состояния (i+1,0) и (i-1, 2);
- из состояния (i, 1) в состояния (i+1,0) и (i-1, 2);
- из состояния (i, 2) в состояния (i+1,1) и (i-1, 3);
- из состояния (i, 3) в состояния (i+1,4) и (i-1, 3).

Рис. 5.18 - Графы поведения дискретной системы

Рассмотренные примеры показывают, что графовые модели являются достаточно мощным средством исследования дискретных САУ. Они не только наглядно иллюстрируют динамику системы, но и позволяют определить основные ее характеристики. Например, с помощью графов на рис. 5.18 можно провести расчет быстродействия системы, оценить ее устойчивость и точностные характеристики.

Контрольные вопросы

1. Характеристика основных типов дискретных САУ.
2. Способы квантования (примеры).
3. Импульсные САУ. Виды модуляции. Особенности цифровых САУ. Кодоимпульсная модуляция.
4. Весовая (импульсная переходная) функция дискретной линейной системы. Весовые коэффициенты дискретных линейных систем. Особенности описания стационарных дискретных линейных систем.
5. Передаточная функция стационарной дискретной импульсной линейной САУ с дискретным выходом.
6. Частотная характеристика стационарной дискретной
импульсной линейной САУ с дискретным выходом. 7.2- преобразование и его свойства.
8. Передаточная функция стационарной дискретной импульсной линейной САУ с непрерывным выходом.
9. Определение разностного уравнения. Разностные уравнения, описывающие дискретную линейную САУ.
10. Анализ возможности исследования цифровых САУ методами теории импульсных САУ.
11. Операторная форма линейных разностных уравнений.
12. Квантование в приближении нулевого порядка уравнений состояния САУ.
13. Решение уравнения состояния дискретной САУ. Преобразование моделей дискретных систем в пространстве состояний.
14. Преобразование разностных уравнений состояния в разностные уравнения типа "вход - выход". Основные теоремы.
15. Устойчивость дискретных линейных систем. Критерии устойчивости стационарных дискретных линейных систем. Функции Ляпунова для дискретной линейной САУ.
16. Понятия управляемости, достижимости и наблюдаемости дискретной линейной САУ. Критерии управляемости и наблюдаемости.
17. Декомпозиция Калмана.
18. Потеря достижимости и управляемости при квантовании.
19. Способ преобразования конечномерного дискретного
пространства состояний в двухмерное пространство состояний.
20. Графовые модели поведения дискретных САУ.

 

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ

 

6.1 Общие сведения об оптимальном управлении и задачи синтеза оптимальных САУ

В инженерной практике и, в частности, в ТАУ нередко возникают задачи о нахождении в некотором смысле наивыгоднейшего (оптимального) режима работы того или иного устройства. С математической точки зрения в таких задачах обычно требуется найти экстремум (максимум или минимум) некоторой величины при каких-нибудь ограничениях.
Включению в число экстремальных широкого круга задач управления способствовали работы А.А. Фельдбаума (1953г.), посвященные исследованию быстродействия САУ. А.А. Фельд-баум первый понял общий характер данной задачи управления и поставил вопрос о ее решении перед математиками (Л.С. Пон-трягиным и др.). Работы Л.С. Понтрягина и его учеников сыграли выдающуюся роль в развитии теории оптимального управления. Сформулированное ими решение задачи оптимального управления получило во всем мире название принципа максимума Понтрягина.
Независимо от русских работ в США Р. Беллман разработал свой метод решения задач управления в вариационной постановке, получивший название метода динамического программирования.
Вариационная постановка задачи управления вызвала огромное число публикаций разных авторов во многих странах мира, но среди них необходимо выделить нашего соотечественника Л.И. Розоноэра, который первым опубликовал в 1959 г. доказательство принципа максимума Понтрягина и обратил внимание на аналогию между принципом максимума Понтрягина и динамическим программированием Беллмана, с одной стороны, и между уравнениями Гамильтона и уравнениями Га-мильтона-Якоби классической механики, с другой стороны. В настоящее время теория оптимального управления и оптимизационная идеология проникли во многие научные исследования и конструкторские разработки, и без преувеличения можно сказать, что язык теории оптимального управления стал общим языком современной теории автоматического управления (СТАУ).
Итак, из вышеизложенного следует, что оптимальными САУ называются САУ, наилучшие в том или ином смысле. Эти системы могут быть как с обратными связями, так и без них (рис. 6.1, а, б).
На этом рисунке использованы обозначения рис. 1.5: g - задающее воздействие; u - управление; f₁, f₂, f₃- возмущения, действующие на систему; К₁, К₂, К₃ - операторы, определяющие преобразование функций g, u, у совместно с возмущениями в каналах связи системы.

Рис. 6.1 - Структурные схемы оптимальных САУ

Синтез оптимальных САУ включает в себя следующие задачи:
- определение математической модели ОУ, т.е. определение функциональной зависимости выходной величины у от входного воздействия на объект u_f, которая может быть задана различными способами, и в частности системой дифференциальных уравнений;
- оценку ограничений, как внутренних, присущих физическим процессам в ОУ, так и внешних, наложенных искусственно;
- определение желаемого поведения ОУ;
- задание определенной цели управления и выбор в соответствии с этой целью критерия оптимальности, характеризующего эффективность управления;
- определение стратегии УУ, т.е. такого алгоритма его работы, который при указанных выше условиях обеспечивает экстремум критерия оптимальности, т.е. максимальную эффективность управления;
- схемную реализацию УУ в соответствии с найденным алгоритмом его работы.
Синтез оптимальных САУ имеет ряд особенностей по сравнению с синтезом других систем. Во-первых, его цель - создание САУ, в которых используются все их возможности для достижения экстремальных значений наиболее важных показателей качества управления при удовлетворении заданных требований к остальным показателям. Во-вторых, при синтезе оптимальных САУ энергетические, механические и другие ограничения учитываются как факторы, определяющие возможности САУ по реализации экстремальных значений заданных показателей качества управления. Экстремальное значение одного из показателей качества управления оптимальной САУ реализуется только в том случае, если управляющее воздействие на ОУ и некоторые его координаты достигают ограничения и остаются определенное время ограниченными в процессе отработки задающего воздействия на систему, т.е. при оптимизации одного из качеств (свойств) системы обычно накладываются ограничения на другие ее свойства. Например, может быть предъявлено требование максимальной точности системы при одновременном ограничении ее быстродействия, стоимости и веса. В-третьих, качество синтезируемой оптимальной САУ зависит от правильности выбора критерия оптимальности, характеризующего эффективность управления, а достижение экстремума этого критерия является целью управления. Обоснование выбора того или иного критерия оптимальности связано с конкретными технико-экономическими условиями работы САУ и в теории оптимального управления не рассматривается.
Любой критерий оптимальности есть аналитическая оценка оптимизируемого качества системы, зависящая от ее параметров, задающего g и возмущающих f_f, f₂, f₃ воздействий на нее и управляющего воздействия и на ОУ.
Следовательно, критерий качества выражается в виде функционала I(u), зависящего от функции управления u, а оптимальное управление u* определяется как функция, реализующая экстремум критерия качества, т.е. функционала I(u). Например, если к системе (см. рис. 6.1, б) предъявляется требование максимальной точности при условии f₁ = f₃ = 0, то критерием оптимальности может служить интеграл
(6.1)
Так как выходная величина объекта y(t) связана с возмущением f₂ и управлением u(t) зависимостью, определяемой системой дифференциальных уравнений объекта, то формула (6.1) может быть записана в следующем виде:

Минимальная ошибка будет в САУ, УУ которой формирует управление u*, при котором выполняется равенство

Такое управление называется оптимальным. Отклонение критерия I(u) от экстремального значения может служить мерой ухудшения качества системы.
Обычно ставится задача достижения экстремума одного функционала, но при этом могут накладываться дополнительные условия и ограничения на любые другие функции и функционалы. Например, можно потребовать выбора такого управления и, чтобы функционал I₁(u) достигал минимума, а другие два функционала I₁(u) и I₁(u) не отклонялись от своих экстремумов более чем на ε₂ и ε₃ соответственно. Оптимальная САУ решает задачу достижения экстремума одного критерия оптимальности, однако принятый в качестве этого критерия функционал может представлять любую желаемую комбинацию оценок различных качеств синтезируемой системы, следовательно, в таком случае оптимизироваться будет не одно качество, а определенная их совокупность. Как правило, критерии оптимальности строятся так, чтобы цель управления достигалась при достижении минимума критерия.
Задачи синтеза оптимальных систем делятся на два класса:
1) оптимизация программы управления, или определение оптимального управления u(t) как функции времени, переводящего ОУ из начального состояния в заданное и реализующего минимум критерия качества, т.е. определение алгоритма УУ системы, схема которой приведена на рис. 6.1, а;
2) определение закона управления как функции фазовых координат ОУ u(у), обеспечивающего движение ОУ по фазовой траектории, на которой реализуется минимум критерия оптимальности, т.е. определение алгоритма УУ замкнутой системы, схема которой приведена на рис. 6.1, б.
Первый класс задач чаще всего используется как первый этап решения задач второго класса. Частным случаем второго класса задач является задача аналитического конструирования регуляторов. Такое название получила методика определения алгоритма УУ в замкнутой системе, схема которой приведена на рис. 6.1, б, при условии, что возмущения f₁ и f₃ отсутствуют, а возмущение f₂, представляет собой последовательность скачкообразных функций времени, ограниченных по модулю, |f_2k(t)| ≤ N = const (k=l,2,...,r).
УУ должно обеспечивать оптимальные показатели качества переходного процесса при ликвидации отклонений изображающей точки ОУ от программной траектории при заданных ограничениях на управление.
В настоящее время существует несколько направлений классификации оптимальных систем. При классификации по оптимизируемым показателям качества САУ различают следующие типы систем:
- оптимальные по быстродействию;
- оптимальные по расходу ресурсов;
- с минимальной энергией управления;
- с минимальными потерями управления.
При определении принципа действия перечисленных типов систем целесообразно использовать понятие n-мерного пространства состояний (фазового пространства), в качестве координат которого выбираются п линейно независимых функций, полностью определяющих изменение состояния системы во времени. В частности, это могут быть функции, относительно которых записывается нормальная система дифференциальных уравнений ОУ. Тогда состояние системы в каждый момент времени будет определяться точкой в ее фазовом пространстве, а изменение состояния системы характеризуется траекторией ее изображающей точки.
Используя понятие фазового пространства, можно дать определения указанных выше типов оптимальных систем в наиболее компактной форме.
Оптимальными по быстродействию называют системы, УУ которых формирует такое допустимое управление u(t) , которое переводит в фазовом пространстве изображающую точку ОУ из одного заданного состояния y(t₀) в другое у(Т) за минимальное время T-t₀.
Системы, оптимальные по расходу ресурсов, переводят в фазовом пространстве изображающую точку ОУ из начального состояния в заданную область V с минимальными затратами ресурсов (топлива, катализатора и т.п.).
Системами с минимальной энергией управления называют системы, которые при переводе изображающей точки ОУ из начального положения в заданное обеспечивают минимум функционала
Системы с минимальными потерями управления, переводя изображающую точку ОУ из начального состояния в заданное, минимизируют отклонение действительных координат объекта от предписанных значений. К этому типу систем, в частности, относятся следящие системы с минимальными ошибками воспроизведения задающего воздействия.
Вторым направлением классификации оптимальных систем является классификация по характеристикам ОУ. Системы делятся на непрерывные, дискретно-непрерывные и дискретные.
В непрерывных системах координаты ОУ и воздействия на него не квантованы ни по времени, ни по уровню. В дискретно-непрерывных системах эти величины квантованы по времени, а в дискретных - и по времени, и по уровню.
Различают оптимальные системы и по типам дифференциальных уравнений ОУ и делят их на системы с линейными, нелинейными объектами и объектами с распределенными параметрами, динамика которых описывается дифференциальными уравнениями в частных производных.
Важными характеристиками ОУ являются ограничения, накладываемые на управление u(t), на его координаты и на возмущения, действующие на него. Поэтому при определении классов оптимальных систем различают:
- системы с ограничением на управление, когда в системе должны выполняться неравенства
|u₁| ≤ M₁, |u₂| ≤ M₂,… , |u_m| ≤ M_m, (6.2)
где М₁, М₂,..., М_m - заданные константы;
- системы с ограничениями на координаты ОУ и с ограничениями на возмущения; ограничения на координаты и возмущения могут накладываться как в виде неравенств (6.2), так и в виде ограничений на функционалы координат и возмущений.
Третьим направлением классификации оптимальных систем является классификация по характеру критерия оптимальности. При этом различают следующие типы систем: равномерно - оптимальные; статистически - оптимальные; минимаксно - оптимальные.
К первому типу относятся такие системы, процессы в которых в каждом отдельном случае являются оптимальными. Например, равномерно-оптимальная по расходу топлива система ориентации космического корабля будет переводить его из любого произвольного положения в заданное с минимальным расходом топлива.
Системы второго типа оптимальны не в каждом отдельном случае, а в среднем, т.е. они дадут наилучший средний результат по сравнению с неоптимальными системами при большом количестве опытов. Критерий оптимальности этого типа систем имеет статистический характер. К ним относятся системы, на процессы в которых так или иначе влияют случайные факторы.
Минимаксно-оптимальные системы обеспечивают наилучший по сравнению с неоптимальными САУ результат только в наихудшем случае, т.е. наихудший результат в такой системе лучше, чем наихудший результат в неоптимальной системе.
Для определения алгоритма работы УУ оптимальной системы необходимо, чтобы это устройство имело следующую информацию об ОУ (см. рис. 6.1):
- об операторе ОУ, т.е. о зависимости у = F(u,f₂);
- о возмущении f₁, действующем на ОУ;
- о состоянии ОУ, или информацию о его фазовых координатах (переменных состояния);
- о критерии оптимальности;
- о задающем воздействии g.
В зависимости от полноты и характера информации, поступающей на УУ, оптимальные системы делятся на три типа:
1) оптимальные системы с полной или максимально возможной информацией об ОУ;
2) оптимальные системы с неполной информацией об ОУ и независимым (пассивным) ее накоплением в процессе управления;
3) оптимальные системы с неполной информацией об ОУ и активным ее накоплением в процессе управления. При этом предполагается, что в УУ всех трех типов систем раложена полная информация об операторе объекта и о критерии оптимальности.
Если кроме этого в УУ имеется полная информация о задающем воздействии g(t) (см. рис. 6.1), о возмущении f₂, приложенном к ОУ, и полная текущая информация о состоянии у ОУ в данный момент времени t, а возмущения f₁ и f₃ отсутствуют, то такая оптимальная система принадлежит к первому типу.
Полная информация о задающем воздействии означает полные сведения о поведении этой функции в прошлом, настоящем и будущем, т.е. знание зависимости, позволяющей получить ее значения в любой момент времени.
Полная информация о текущих значениях фазовых координат позволяет определить все поведение объекта в будущем. Очевидно, на практике в большинстве случаев информацию об ОУ нельзя считать полной.
Отсутствие полной информации об ОУ, задающих и возмущающих воздействиях вынуждает рассматривать системы второго и третьего типов.
В системах второго типа в УУ используется информация не о самих воздействиях, а лишь статистические характеристики случайных задающих воздействий и случайных возмущений, действующих на объект. Структурная схема оптимальной системы в этом случае может иметь вид, изображенный на рис. 6.1, а и б, при условии, что f₃=0, а помеха f₂ аддитивно смешивается с воздействиями на объект. Для выбора оптимального алгоритма УУ необходимо знание максимально возможной информации о задающих воздействиях и возмущениях.
Накопление этой информации в системах второго типа осуществляется путем наблюдения и не зависит от алгоритма УУ. Накопленная информация используется для построения гипотез о воздействиях на объект и для перестройки в соответствии с этими гипотезами параметров УУ.
К системам третьего типа относятся системы со структурной схемой, представленной на рис. 6.1, б. В них управление u(t) решает следующие задачи:
- осуществляет такое изменение состояния объекта, при котором происходит накопление максимума информации о неизвестных характеристиках объекта, воздействиях и возмущениях;
- переводит ОУ из начального состояния в заданное по фазовой траектории, на которой реализуется минимум критерия оптимальности.
В связи с двойственным характером управление в системах третьего типа называется дуальным. Системы второго и третьего типов называют также оптимальными системами с адаптацией, так как в них в процессе управления осуществляется изучение условий работы системы, накопление информации об этих условиях, изменение закона управления на основании полученной информации, и, таким образом, эти системы приближаются к системам с полной информацией.
Практическая реализация оптимальных систем со сложными ОУ требует применения в УУ вычислительных устройств, выполняющих расчетные и логические операции. Для упрощения решения задач синтеза подобных САУ целесообразно использовать квазиоптимальные системы управления.
Квазиоптимальными или субоптимальными (близкими к оптимальным) называют САУ, алгоритм УУ которых получен путем сравнительно небольших отступлений от оптимального алгоритма. При этом УУ таких САУ может реализоваться по достаточно простой схеме без сложных вычислительных устройств.
Задача синтеза оптимальных САУ, а точнее, задача определения алгоритма УУ САУ относится к классу вариационных задач, для решения которых наиболее широко используются следующие методы:
- классического вариационного исчисления;
- принципа максимума Понтрягина;
- динамического программирования;
- Винера - Колмогорова и Калмана - Бьюси;
- оптимизации критерия обобщенной работы;
- функционального анализа;
- метрического анализа.
Далее рассматриваются первые три метода решения вариационных задач оптимального управления с полной информацией, а также оптимальные системы с неполной информацией (с адаптацией).

6.2 Вариационное исчисление и его использование в теории оптимальных САУ

Методы вариационного исчисления позволяют найти условия, при которых достигается экстремум критерия оптимальности, записанного в виде некоторого функционала. Условия получаются в виде некоторой системы уравнений относительно управления и переменных состояния ОУ (фазовых координат объекта). Решение этой системы, удовлетворяющее граничным условиям, определяет оптимальное управление и оптимальную траекторию изображающей точки ОУ в его пространстве состояний. При записи условий существования экстремума функционала используются следующие понятия и определения.
1. Функционал - переменная величина I, зависящая от функций
(i = l,2,...,m; j = 1,2,...,n) . (6.3)
При этом каждой из функций (6.3), взятой из некоторого класса этих функций, соответствует определенное значение функционала I, что записывается в виде

2. Приращение, или вариация, δu_i, аргумента u_i(t) функционала (6.4) есть разность функций

где - новая произвольно выбранная функция из класса функций u_i(t).
3. Близость двух функций характеризуется определенным порядком близости.
Например, функции u₁(t) и близки в смысле близости нулевого порядка, если модуль разности u₁(t) - мал (рис. 6.2, а); функции u₂(t) и близки в смысле близости первого порядка, если модули разностей u₂(t) - и малы (рис. 6.2, б).
4. Функционал (6.4) называется непрерывным при в смысле близости k-гo порядка, если для любого положительного ε можно подобрать такое δ > 0, что

Функции u_i(t) берутся из класса функций, на котором функционал (6.4) определен.

Рис. 6.2 - Функции нулевого и первого порядков близости

5. Приращение функционала (6.4), соответствующее вариациям аргументов

определяется в виде
(6.5)
Если функционал (6.4) имеет в некоторой области непрерывные частные производные второго порядка, то его приращение (6.5) может быть разложено в ряд Тейлора:

Представление приращения функционала (6.4) в форме (6.6) позволяет достаточно просто определить его вариации.
6. Если приращение функционала ∆I может быть представлено рядом Тейлора (6.6), то линейная по отношению к вариациям аргументов часть приращения функционала называется первой вариацией функционала и записывается в виде

7. Второй вариацией функционала (6.4) называется функция

Необходимым условием существования экстремума непрерывного функционала является равенство нулю его первой вариации:
δI=0. (6.7)
Если достигается минимум функционала, то выполнение условия (6.7) должно сопровождаться выполнением необходимого условия δ²I ≥ 0, а в случае достижения максимума - условия δ²I ≤ 0.
Приведенные необходимые условия существования экстремума функционала справедливы, если непрерывный функционал определен на открытом множестве функций, или если функционал определен на замкнутом множестве функций, то экстремум функционала реализуется функциями, не принадлежащими границе множества. Особенности определения необходимых условий существования экстремума функционала в случае, когда этот экстремум реализуется функциями, частично или полностью принадлежащими границе множества, на котором этот функционал определен, будут рассмотрены ниже.
В подавляющем большинстве случаев критерий оптимальности записывается в виде интеграла. В частности, он может быть записан так:
(6.8)
где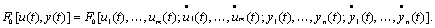
Если подынтегральная функция F₀[u(t), y(t)] непрерывна по совокупности ее аргументов и существуют все ее частные производные до третьего порядка включительно, то необходимые условия экстремума функционала (6.8) записываются в виде системы дифференциальных уравнений Эйлера - Лагранжа:

Условие (6.9) эквивалентно условию (6.7). Поэтому только на интегральных кривых уравнений Эйлера-Лагранока, удовлетворяющих граничным условиям

может реализоваться экстремум функционала (6.8).
Интегральные кривые уравнений Эйлера-Лагранжа называются экстремалями. Экстремали, удовлетворяющие граничным условиям, определяются путем решения краевой задачи. Следует помнить, что это решение не всегда существуем, а если и существует, то может быть не единственным. Однако во многих задачах синтеза оптимальных САУ из физического или геометрического смысла задачи достаточно просто устанавливается существование решения, его единственность и то, что оно реализует минимум критерия оптимальности. В этом случае экстремали, удовлетворяющие граничным условиям, есть решение оптимальной задачи.
Если же существует несколько решений уравнения (6.9), удовлетворяющих граничным условиям (6.10), то путем вычисления значений критерия оптимальности на каждом из полученных решений выбирается то из них, на котором критерий достигает минимума.
Экстремум функционала (6.8) может достигаться не на гладких, а на кусочно-гладких экстремалях с конечным числом угловых точек.
Угловыми точками называют точки, в которых экстремали непрерывны:

а производные от экстремалей терпят разрывы первого рода (рис. 6.3):

где - соответственно, левые и правые пределы экстремалей и их производных в k-й угловой точке.

Рис. 6.3 - Экстремаль с угловыми точками

Если экстремум функционала реализуется на экстремалях с угловыми точками, которые называются ломаными экстремалями, то в каждой угловой точке должны выполняться условия Вейерштрасса - Эрдмана:

В теории оптимальных САУ возникают задачи, когда одна или обе граничные точки экстремалей перемещаются по определенному закону. Например, ракетой А (рис. 6.4) надо управлять так, чтобы уничтожить ракету В за минимальное время. Ракета А запускается с самолета. Очевидно, что в этом случае могут быть заданы только начальные условия (координаты ракет А и В, значения их скоростей, ускорений в момент старта) и не могут быть заданы граничные условия, т.е. указанные выше параметры в момент встречи двух ракет, так как последние зависят от искомого минимального времени Т* сближения ракет А и В.

Рис 6.4 - Задача перехвата ракеты В ракетой А за минимальное время

Подобные задачи в вариационном исчислении называются задачами с подвижными концами или границами (выше рассматривалась задача с закрепленными концами). В таких задачах необходимые условия существования экстремума функционала (6.9) должны быть дополнены условиями:

если не задан закон перемещения концевых точек,

(6.11)
где - закон перемещения концевой точки экстремали y_j(t₀);
- закон перемещения концевой точки экстремали у_j(Т).
Условия (6.11) носят название условий трансверсальности.
В большинстве случаев при синтезе оптимальных САУ возникают задачи минимизации критерия оптимальности при дополнительных условиях, наложенных на координаты ОУ и на граничные условия. В классическом вариационном исчислении такие задачи получили название задач на условный экстремум.
Простейшая задача на условный экстремум формулируется так: требуется исследовать на экстремум функционал (6.8) при условии, что экстремали, на которых реализуется минимум функционала, должны удовлетворять системе дифференциальных уравнений
F_j(t, y₁, y₂, ..., y_n) = 0 (у=1,2,..,n), (6.12)
которую называют системой уравнений связи. Эта задача решается путем преобразования функционала (6.8) к виду
(6.13)
где
λ_j - неопределенные множители Лагранжа, и исследования нового функционала (6.13) на безусловный экстремум.
Необходимые условия существования безусловного экстремума функционала (6.13) и, следовательно, условного экстремума функционала (6.8) имеют вид

где (6.14) - система уравнений Эйлера - Лагранжа, (6.15) - система дифференциальных уравнений связи.
Условия (6.14) и (6.15) состоят из (2n+m) уравнений относительно (2n+m) неизвестных u₁, ..., u_m; у₁, ..., у_n; ╏, ..., λn и, следовательно, позволяют определить эти неизвестные функции. Решения систем уравнений (6.14) и (6.15) будут содержать 2(2n+m) неизвестных постоянных интегрирования. С помощью 2(n+m) граничных условий, заданных для экстремалей u_i(t) и y_j(t) , можно определить 2(n+m) постоянных интегрирования. Остальные 2n постоянных интегрирования находятся путем подбора 2n незаданных граничных условий для множителей Лагранжа λ_j таким образом, чтобы удовлетворялись граничные условия для функций u_j(t) и у_j(t) .
Иногда при решении вариационных задач на условный экстремум возникает необходимость выбора из класса кусочно-гладких вектор-функций u(t), y(t) тех, которые доставляют экстремум функционалу

и удовлетворяют уравнениям связи (6.12) и условиям на концах

Такую задачу называют задачей Больца.
Применение методов классического вариационного исчисления для решения задач синтеза оптимальных САУ ограничено следующими трудностями.
Во-первых, в реальных системах допустимые управляющие воздействия принадлежат замкнутому множеству функций, т.е. удовлетворяют условиям вида (6.2), и чаще всего наилучшие результаты получаются в том случае, если оптимальные управления выбираются из числа функций, частично или полностью принадлежащих границе этого множества. Например, управляющее напряжение на входе оптимального по быстродействию электропривода, динамика которого описывается дифференциальным уравнением второго порядка, должно изменяться так, как это показано на рис. 6.5.

Рис. 6.5 - График изменения напряжения на выходе оптимального по быстродействию электропривода

При этом оказывается, что минимум критерия оптимальности, являющегося функционалом от управления u(t) , достигается при |u(t)| = М = const, хотя при этих условиях первая вариация функционала не равна нулю (рис. 6.6).

Рис. 6.6 - График зависимости величины функционала I(u) от модуля управления |u(t)|

Во-вторых, если оптимальное управление принадлежит к классу кусочно-постоянных функций с конечным числом точек разрывов первого рода (например, рис. 6.5), то это создает значительные вычислительные трудности при определении алгоритма УУ оптимальной САУ.

Первая из отмеченных выше трудностей преодолевается путем замены замкнутого множества допустимых управлений открытым. Такая замена может быть осуществлена, в частности с помощью "функций штрафа" или функций, предложенных Мьеле. При использовании "функций штрафа", в критерий оптимальности вводится дополнительная функция от управления, которая вызывает резкое увеличение критерия, если управление превышает допустимое значение, т.е. "штрафует" за "нарушение". Если на управление наложено ограничение
|u(t)| ≤ М = const, (6.16)
то "функция штрафа" может быть выбрана в виде

Используя функцию (6.17), можно методами классического вариационного исчисления определять условия существования минимума критерия оптимальности и в случае, когда оптимальное управление выбирается из замкнутого множества допустимых управлений.
При использовании функций Мьеле ограничение вида (6.16) учитывается с помощью замены управления u(t) функцией
(6.18)
Изложим постановку задачи определения алгоритма УУ различных типов САУ на основе методов классического вариационного исчисления.

6.2.1 Системы, оптимальные по быстродействию

Задана система дифференциальных уравнений, описывающая динамику ОУ:
= F_j(y₁, y₂, ..., y_n; u₁, u₂, ..., u_m) (j=1,2,...n), (6.19)
где y_j - координаты ОУ; u_i - управляющие воздействия.
На управляющие воздействия наложены ограничения
|u₁| ≤ М₁, |u2| ≤ М₂, ..., |u_m| ≤ М_m, (6.20)
где М₁, М₂, ..., М_m - заданные константы.

Необходимо найти функции u_i = u_i(t) (в разомкнутой системе) или u_i = u_i(y₁, y₂, ..., y_n) (в замкнутой системе), удовлетворяющие офаничениям (6.20), переводящие ОУ из начального состояния {y₁(t₀), ..., y_n(t₀)} в заданное Y_T{y₁(T), ..., y_n(T)} и обеспечивающие минимум функционала (критерия оптимальности)
(6.21)
где Т- незаданное время перехода ОУ из состояния в состояние Y_T.
Минимум функционала (6.21) обеспечивается при минимальном времени перехода ОУ из начального состояния в заданное. Так как экстремали функционала (6.21) должны удовлетворять системе уравнений (6.19), то поставленная задача является вариационной задачей на условный экстремум функционала (6.21).

6.2.2 Системы, оптимальные по расходу ресурсов

Такие САУ разрабатываются для управления различными типами ракет и управляемых космических аппаратов, а также для определения оптимальных режимов полета самолетов и режимов работы химических и металлургических промышленных установок.
Как и в предыдущей задаче, заданы система дифференциальных уравнений динамики ОУ (6.19), ограничение на управление (6.20) и граничные условия , Y_T. Кроме того, полагается известной связь скорости расхода топлива с управляющими воздействиями u_i. Часто эта зависимость имеет вид

Тогда общее количество топлива I, израсходованного на временном интервале [t₀, T], определяется функционалом
(6.22)
Как и в предыдущем случае, задача заключается в выборе из замкнутого множества функций (6.20) таких управляющих воздействий u_i = u_i(t) или u_i = u_i(y₁, y₂, ..., y_n), которые переводят ОУ из начального состояния в заданное так, чтобы функционал (6.22) принимал минимальное значение. При этом время достижения конечного состояния Т может быть как неограниченным, так и ограниченным. Данная задача, как и предыдущая, является задачей на условный экстремум.

6.2.3 Системы, оптимальные по расходу ресурсов

Постановка задачи синтеза таких систем не отличается от постановки предыдущей задачи, за исключением минимизируемого критерия оптимальности, который в этой задаче имеет вид

6.2.4 Системы с минимальными потерями управления

Синтез таких систем получил название аналитического конструирования регуляторов. При решении этой задачи, как и ранее, полагается, что заданы система уравнений динамики ОУ (6.19), ограничения (6.20) и естественные граничные условия:

которые означают, что синтезируемое УУ, ликвидируя вызванное скачкообразным возмущающим воздействием отклонение изображающей точки ОУ от программной траектории g(t), должно обеспечить либо минимальное отклонение изображающей точки ОУ от программной траектории, либо возвращение на эту траекторию по окончании переходного процесса. В последнем случае граничные условия (6.23, б) запишутся в виде
y₁(∞) = ... = y_n(∞) = u₁(∞) = ... u_m(∞) = 0 .
Системы с минимальными потерями управления решают задачу оптимальной отработки отклонений изображающей точки ОУ от программной траектории, поэтому при синтезе УУ можно положить задающее воздействие на систему g(t) (см.рис. 6.1, б)
равным нулю. Тогда составляющие вектора y(t) будут равны составляющим вектора ошибки системы z(t).
Задачей аналитического конструирования регуляторов является определение закона управления в форме дифференциального уравнения вида f(... , u, y(t), t) = 0 , такого, чтобы УУ, присоединенное к ОУ, обеспечивало минимум функционала
(6.24)
где - положительно определенная квадратичная форма; G - функция, оптимизирующая конечное состояние системы и равная нулю при T = ∞ на всевозможных допустимых возмущенных движениях, возникающих в области определения уравнений (6.19) с учетом ограничений, наложенных на управление и координаты ОУ.
Критерий оптимальности (6.24) характеризует взвешенные по константам а_i, с_i, k_i интегральную квадратичную ошибку и затраты энергии на управление, т.е. является интегральной квадратичной функцией потерь управления. При аналитическом конструировании регуляторов по-прежнему решается вариационная задача на условный экстремум. Определение алгоритма УУ, реализующего минимум функционала (6.24), имеет две особенности:
- во-первых, в результате решения систем уравнений (6.14) и (6.15), определяющих необходимые условия существования минимума функционала (6.24), находится дифференциальное уравнение физически нереализуемого оптимального УУ, так как его характеристическое уравнение имеет как отрицательные, так и положительные корни. Поэтому синтезируемое УУ реализуется по алгоритму, полученному из уравнения оптимального УУ путем отбрасывания в его решении экспоненциальных членов с положительными показателями;
- во-вторых, решение вариационной задачи позволяет определить закон управления, реализующий минимум функционала (6.24), однако построенное по этому закону УУ может и не обеспечивать переходный процесс при отработке возмущений начальных условий (6.23, а) с оптимальными или требуемыми показателями их качества. Показатели качества переходного процесса зависят от выбора констант а_i, c_i, , k_i критерия оптимальности (6.24). Задать значения констант, обеспечивающих: оптимальные показатели качества переходных процессов в системе, в начале решения вариационной задачи трудно. Поэтому константы определяются так: находится уравнение УУ, коэффициенты которого будут функциями констант a_i, c_i, k_i, записываются показатели качества переходного процесса как функции параметров системы и определяются значения констант, дающие минимум наиболее важному показателю качества при ограничениях на остальные показатели. Доказано, что в результате решения перечисленных выше четырех задач для ОУ с минимально-фазовыми передаточными функциями оптимальное управление должно иметь вид:
а) в системах, оптимальных по быстродействию,
(6.25)
б) в системах, оптимальных по расходу ресурсов,

в) в системах с минимальной энергией управления и минимальными потерями управления

Из равенства (6.25) следует, что в системах, оптимальных по быстродействию, схему УУ можно представить в виде, изображенном на рис. 6.7.

Рис. 6.7 - УУ САУ, оптимальной по быстродействию

Число интервалов знакопостоянства функции , а следовательно, и оптимального управления не превы шает порядка дифференциального уравнения динамики линейного ОУ, если его характеристическое уравнение имеет только действительные отрицательные корни. Для оптимальных по быстродействию систем при тех же допущениях и практически возможных граничных условиях А.А. Фельдбаум доказал теорему об n-интервалах, согласно которой при таких условиях число интервалов знакопостоянства оптимального управления равно порядку дифференциального уравнения ОУ.
Так как в САУ, оптимальных по быстродействию, исполнительный элемент УУ (см. рис. 6.7) имеет релейную характеристику, то теорема об n-интервалах может быть сформулирована так: оптимальное по быстродействию управление линейным объектом, характеристическое уравнение которого имеет только действительные отрицательные корни, должно иметь (n-1) переключение, где n - порядок дифференциального уравнения ОУ.
Если характеристическое уравнение ОУ имеет комплексно - сопряженные корни, то число интервалов знакопостоянства оптимального управления может превышать порядок дифференциального уравнения динамики объекта. Однако, если интервал оптимального процесса не превышает половины периода собственных колебаний объекта на высшей частоте, то сформулированное утверждение не будет выполняться. Методами классического вариационного исчисления доказано, что все приведенные выше выводы о свойствах оптимального управления линейными объектами распространяются на оптимальное по быстродействию управление нелинейными объектами, содержащими нелинейные элементы типа люфта, сухого трения и зоны нечувствительности. Методики определения алгоритмов УУ САУ, оптимальных по быстродействию и оптимальных по расходу ресурсов, не имеют принципиальных отличий. Также мало отличаются методики определения алгоритмов УУ систем третьего и четвертого типов. Поэтому рассмотрим примеры определения алгоритмов УУ только систем, оптимальных по быстродействию, и систем с минимальными потерями управления.
Пример 6.1. Алгоритм УУ САУ, оптимальной по быстродействию, создает такое управление u(t) , что в результате его воздействия на ОУ переходный процесс в системе заканчивается за минимальное время. Передаточная функция ОУ имеет вид W(p) = K_v/p(1+T₁p). Динамика ОУ описывается системой дифференциальных уравнений:
На управление наложено ограничение |u(t)| ≤ М.
Заданы граничные условия:

Решение. В соответствии с методикой решения вариационных задач на условный экстремум записывается функционал в виде
(6.27)
где L(u) - "функция штрафа" (6.17).
Необходимые условия существования экстремума функционала (6.27) записываются в следующей форме:
(6.28)
Из первых двух уравнений системы (6.28) находится
(6.29)
Решение третьего уравнения (6.28) с учетом функции (рис.6.8) при имеет вид
(6.30)

Рис. 6.8 - График частной производной от "функции штрафа" по управляющему воздействию u(t)

 

Из равенства (6.30) следует, что оптимальное управление u*(t) - кусочно-постоянная функция, имеющая не более двух интервалов знакопостоянства, т.е. имеющая не более одного "переключения". Экстремали y₁(i) и y₂(t) можно было бы определить, подставив в пятое уравнение (6.28) значение u(t) из формулы (6.30). Однако при этом возникают следующие трудности: во-первых, постоянные интегрирования А₁ и А₂из выражения (6.29) нельзя определить, так как неизвестны граничные условия для функций λ₁(t) и λ₂(t); во-вторых, после исключения u(t) с помощью равенства (6.30) система четвертого и пятого уравнений (6.28) становится нелинейной и неразрешимой в квадратурах. Поэтому определение экстремалей, на которых реализуется минимум функционала (6.27), т.е. решение краевой задачи, осуществим с помощью метода стыкования решений дифференциальных уравнений, который также называют методом припасовывания. Так как известно, что функция u*(t) - кусочно-постоянная, и неизвестен только ее момент переключения t₁ , то решения системы четвертого и пятого уравнений (6.28) на любом интервале знакопостоянства функции u*(t) будут иметь вид:
(6.31)
С помощью условий (6.26), решений (6.31) и с учетом непрерывности функций y₁(t) и у₂(t) в момент переключения управления t₁ записывается система уравнений:

где

В результате разрешения системы (6.32) относительно произвольных постоянных интегрирования получается система уравнений, связывающая неизвестные t₁ и Т:
(6.33)
с помощью которой находятся эти неизвестные, и таким образом полностью определяется функция u*(t). Следует учитывать, что система уравнений (6.33) имеет не единственное решение, поэтому из совокупности ее решений истинное выбирается с помощью условия 0 < t₁ < Т. Если положить в рассматриваемой задаче T₁ = 1с , K_v = 2с^{-1, М = 5В и воспользоваться последним условием, то решение системы уравнений (6.33) дает результат t}₁ = 0,378с, Т = 0,656с. График функции оптимального управления u*(t) объектом с заданными параметрами приведен на рис. 6.9.

Рис. 6.9 - График функции оптимального по быстродействию уравнения u*(t)

Из графика видно, что УУ следует строить по схеме, изображенной на рис. 6.7, приняв за его входные координаты функции z₁(t), z₂(t), ..., z_n(t). В рассматриваемом случае определение алгоритма УУ сводится к выбору оператора μ(z₁, z₂) и определению его параметров, при которых функция μ(t) меняет знак, в момент t = t₁. Если в качестве фазовых координат системы принять z₁ = z(t) , z₂ = (t) и выбрать оператор μ(z₁, z₂) в виде
(6.34)
то функция μ(t) будет менять знак только один раз как линейная комбинация линейно независимых функций. Чтобы изменение знака μ(t) происходило в момент t₁, коэффициенты оператора (6.34) выбираются из условия
(6.35)
Из уравнения (6.35) следует: k₁/k₀ = -z(t₁)/ (t₁) .
Используя равенство z(t) = x(t) - y(t), зависимости (6.31) и полученное выше значение момента переключения оптимального управления t₁ = 0,378 с при условии, что g(t) = 1(t) , легко найти: z(t₁) = 0,42B, (t₁) = 3,2В/с, k₁/k₀ = 0,131с. Тогда оператор (6.34) можно записать в виде μ(p) = k₀(1 + 0,131p), где k₀ - коэффициент, выбираемый так, чтобы обеспечить требующуюся чувствительность УУ. Очевидно, что при изменении величины задающего воздействия g(t) должен изменяться коэффициент k₁/k₀, поэтому для обеспечения оптимальной по быстродействию отработки любого допустимого значения задающего воздействия g(t) необходимо знать зависимость 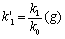и предусмотреть перестройку параметров УУ в соответствии с этой зависимостью. Кусочно-линейную аппроксимацию зависимости 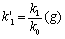можно получить, рассчитав значения k₁', соответствующие различным значениям задающего воздействия, взятым с определенным шагом из множества допустимых задающих воздействий из класса единичных функций, по методике, приведенной выше для случая g(t) = 1(t) .
При практической реализации оптимальных САУ, чтобы избежать автоколебаний в установившемся режиме работы, релейный исполнительный орган УУ заменяется усилительными элементами с характеристиками, изображенными на рис. 6.10 (а - усилительный элемент с ограничением, б - релейно-пропорциональный усилитель).

Рис. 6.10 - Характеристики исполнительных органов систем, оптимальных по быстродействию

Отметим, что использование исполнительных органов с такими характеристиками при определенных условиях позволяет осуществить квазиоптимальное по быстродействию управление объектом без перестройки параметров УУ, так как неточность вывода изображающей точки ОУ в заданную точку фазового пространства в этом случае может быть скомпенсирована наличием области притяжения в окрестности этой точки, обусловленной линейным участком характеристики исполнительного органа УУ.
Пример 6.2. Задача аналитического конструирования регулятора. В соответствии с методикой решения таких задач полагаем g(t)≡0. Возмущенное движение ОУ описывается системой уравнений
(6.36)
Естественные граничные условия заданы в виде:
y₁(0) = y₁₀, …, y_n(0) = y_n0, u(0) = u₀;
y₁(∞) = ... = y_n(∞) = u(∞) = 0.

Эти условия отражают тот факт, что при любых начальных условиях переходный процесс при t=∞ заканчивается приходом изображающей точки системы в начало фазовых координат.
На управление u(t) наложено ограничение |u(t)| ≤ M .
Задачей оптимального управления является обеспечение минимальной интегральной ошибки. В качестве критерия оптимальности выбран интеграл (6.24).
Решение. В соответствии с методикой решения задач на условный экстремум записывается функция

Функция u(t) заменяется на Ф(ζ) (6.18). Необходимые условия существования минимума функционала (6.24) имеют следующий вид:
(6.37)
Из последнего уравнения системы можно сделать вывод,
что если , то |u(t)|=М, а если , то экстремали определяются системой уравнений, полученной из (6.37) при условиях:
(6.38)
Решением системы (6.37) при допущениях (6.38) являются функции y_j(t), λ_j(t), которые будут линейными комбинациями 2n членов вида и , где Re p_i>0. Из граничных условий при t→∞ следует: (i=1,2,...,n).
Тогда функции y_j(t) и λ_j(t) принимают вид:
(6.39)
В результате решения системы уравнений (6.39) относительно функций находится зависимость

Путем подстановки найденных значений λ_i в уравнение определяется u = Q_iy_i + … + Q_ny_n. Это выражение есть алгоритм УУ при |u(t)| < М .
Таким образом, полный алгоритм УУ записывается в виде

Для определения произвольных постоянных интегрирования функций (6.39) на интервале, где |u(t)|<М, и на интервале, где |u(t)| ≥ М, используются граничные условия, условия Вейерштрасса - Эрдмана в угловых точках функции u(t) и условие непрерывности в этих точках.
Вариационные задачи с ограничениями на координаты ОУ решаются теми же методами, что и вариационные задачи с ограничениями на управление.

6.3 Принцип максимума

Изложим вначале геометрическую интерпретацию принципа максимума Л.С. Понтрягина (Рис. 6.11)

Рис. 6.11 - К принципу максимума

Пусть стоит задача о переводе за минимальное время изображающей точки из некоторого начального состояния 0 в определенное конечное состояние К. Каждой точке фазового пространства, окружающего точку К, соответствует определенная оптимальная траектория и отвечающее ей минимальное время перехода в эту точку. Вокруг конечной точки можно построить поверхности, являющиеся геометрическим местом точек с одинаковым минимальным временем t_i перехода в эту точку (рис. 6.11, а). Такие поверхности называются изохронами. Очевидно, что оптимальная по быстродействию траектория из точки 0 в конечную точку К должна быть максимально близка нормалям к изохронам, т.е. должна приближаться к ним настолько близко, насколько это позволяют ограничения, налагаемые на координаты ОУ.
Действительно, всякое движение вдоль изохрон увеличивает время процесса, так как означает дополнительную затрату времени без уменьшения отрезка времени, остающегося до момента достижения конечной точки. Математически это условие оптимальности траектории означает, что на протяжении всей траектории скалярное произведение вектора скорости v = dy/dt на вектор, обратный градиенту времени перехода в конечную точку, должно быть максимально (напомним, что скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними). Если обозначить это произведение через H, а вектор, обратный градиенту времени перехода, через ψ, т.е. ψ = -gradt (см. рис. 6.11, а), то можно записать:
(6.40)
где ψ_i и v_i - координаты векторов ψ = (ψ_i, …, ψ_n) и v=(v₁, ..., v_n), т.е. условием оптимальности является максимум проекции вектора v на направление ψ.
Сформулированное условие оптимальности и есть принцип максимума Л.С. Понтрягина.
При использовании принципа максимума движение ОУ обычно представляется в виде системы обыкновенных дифференциальных уравнений
= Fj(y₁, ..., y_n; u₁, ..., u_m; t), (6.41)
где y₁, ..., y_n - фазовые координаты;
u₁, ..., u_m - управляющие воздействия;
t - время.
Допустимыми считаются управления u₁, ..., u_m, которые являются непрерывными для всех рассматриваемых t, за исключением конечного числа моментов, где они могут претерпевать разрывы первого рода. На участках непрерывности и в точках разрыва управления они могут принимать лишь конечные значения. Кроме того, на каждое из управлений могут накладываться дополнительные ограничения вида
u_imin ≤ u_i ≤ u_imax (i=1,2,…, m).
Задача оптимального управления сводится к отысканию таких управлений, удовлетворяющих наложенным ограничениям, которые одновременно с переводом объекта (системы) из одного положения в другое обеспечивают экстремум выбранного функционала качества. При этом задача может решаться применительно к автономным и неавтономным системам.

6.3.1 Управление автономной системой

Система называется автономной, если правые части дифференциальных уравнений, описывающих ее движение, явно не зависят от времени.
Функционал качества в этом случае выбирается в виде интегрального выражения
(6.42)
где F₀(y₁, ..., у_n; u₁, ..., u_m) - заданная функция.
Задача оптимального управления сводится к минимизации дополнительной координаты
удовлетворяющей условию у₀=0 при t=t₀. В соответствии с выражением (6.42) к системе (6.41) добавляется еще одно уравнение
= F₀(y₁, ..., у_n; u₁, ..., u_m) (6.43)
Далее, вместе с основной системой уравнений, полученной из
(6.41) и (6.43), т.е. = F_j(y₁, ..., у_n; u₁, ..., u_m) (j=0,1,...,n), рассматривается также система сопряженных уравнений для вспомогательных переменных ψ₀, ψ₁,..., ψ_n,:

Введение функции Гамильтона
= (6.44)
позволяет объединить основную и сопряженную системы уравнений одной записью:

6.3.2 Основная теорема (принцип максимума)

Пусть u(t) является управлением, переводящим изображающую точку из начального положения y(t₀) в конечное положение у(Т) , a y(t) - соответствующая этому управлению траектория. Если u(t) оптимально, то найдется такая ненулевая вектор-функция ψ(t), соответствующая u(t) и y(t} , при которой функция Н(у,ψ,u) в любой момент времени, находящийся в заданном интервале [t₀,Т], достигает максимального значения:
(6.47)
Выражение (6.47) используется для определения функции u(t) Управление будет оптимальным, если оно обеспечивает максимум функции H[y(t), ψ(t), u(t)] в любой момент времени.
Следует заметить, что при оптимальном управлении функции H(t) и ψ₀(t) являются постоянными: H(t)=0, ψ₀(t) ≤ 0. Как видно из уравнения (6.47), принцип максимума устанавливает связь между управлением и координатами основной и сопряженной систем.
Геометрическая интерпретация выражений (6.44) и (6.47) дана выше (см. рис.6.11). Величина Н является скалярным произведением векторов ψ и у, поэтому направление движения изображающей точки при оптимальном управлении должно быть таким, чтобы векторы ψ и у являлись ортогональными.

6.3.3 Управление неавтономной системой

Если в правую часть уравнения системы (6.41) явно входит время t, то задача оптимального управления состоит в переводе изображающей точки из начального положения y(t₀) в положение, в котором выполнялись бы условия у_j(t) = у_j(Т) (j=1,2,...,n), где y_j(T) - заданные функции времени.
Задача оптимального управления в этом случае может быть сведена к задаче с заданной точкой, если рассматривать движение системы в фазовом пространстве ошибки: z(t) = у(Т) - y(t),
где z(t) = [z₁(t), z₂(t), ..., z_n(t)]; у(Т) = [у₁(Т), y₂(Т), ..., у_n(Т)].
Задача оптимального быстродействия является частным случаем задачи с закрепленными концами. Задача состоит в том, чтобы среди всех допустимых управлений определить такие u(t), которые переводят изображающую точку из одного положения в другое за минимальное время. За функционал качества принимается интегральное выражение вида , где t₀ и Т - время начала и конца управления. В случае оптимального быстродействия выражение для функции Гамильтона записывается в следующей форме: . Так как во время управления ψ₀=const, то достаточно рассмотреть функцию
Таким образом, при решении задачи оптимального быстродействия максимум функции Гамильтона будет иметь значение большее или равное нулю:

Как и прежде, вектор ψ определяет направление вектора скорости. Однако в этом случае векторы ψ и у могут быть неортогональными.
При определении оптимального управления n(i) решаются
совместно основная (6.45) и сопряженная (6.46) системы уравнений. Для задач с закрепленными концами фазовых траекторий наряду с подбором управления u(t), максимизирующего функцию Н₁(у, ψ, u) в каждой точке оптимальной траектории, необходимо знать начальное состояние объекта y₁(t₀), ..., y_n(t₀) и начальное значение вспомогательного вектора ψ₁(t₀), ..., ψ_n(t₀). Вектор y(t₀) задается условиями задачи, а вектор ψ(t₀) заранее неизвестен. Составляющие вектора ψ_j(t₀) (j=1, 2, ..., n) необходимо подобрать таким образом, чтобы оптимальная траектория прошла через заданную концевую точку у₁(Т), ..., y_n(Т).
Для задач с подвижными концами граничные положения фазовой точки определяются из условий трансверсальности. Условия трансверсальности для левого и правого концов фазовой траектории определяются условиями ортогональности векторов ψ(t₀) и #0968(T) соответственно касательными векторов многообразий [48], связывающих начальные и конечные значения фазовых координат:
φ(y₁, y₂, …, y_n)=0; θ(y₁, y₂, …, y_n) = 0.
Условия трансверсальности дают дополнительные соотношения, необходимые для определения начальной и конечной точек фазовой траектории.
Из принципа максимума вытекают следующие основные положения теории оптимальных быстродействий: оптимальные системы являются системами релейного типа; число переключений оптимального управления конечно и не превышает (n-1) переключений для систем, корни характеристического уравнения которых являются вещественными отрицательными или нулевыми. В случае же комплексных корней характеристического уравнения число корней может быть больше чем (n-1).

6.3.4 Определение оптимальных по быстродействию управлений с помощью принципа максимума

Использование принципа максимума в задачах оптимального быстродействия приводит к краевой задаче для основной (6.45) и сопряженной (6.46) систем дифференциальных уравнений, решение которой представляет большие трудности.
При этом приходится оперировать 2п неизвестными y₁, y₂, ..., y_n; ψ₁, ψ₂, …, ψ_n и 2n краевыми условиями, которыми являются начальные значения векторов y(t₀) и ψ(t₀). Начальные условия y₁(t₀), …, y_n(t) известны, а значения ψ₁(t₀), ..., ψ_n(t₀) неизвестны и подбираются из условия удовлетворения граничным условиям на конце оптимальной траектории.
Общих правил подбора значений ψ₁(t₀),..., ψ_n(t₀) не существует. Однако достаточно широкое применение в этих целях получил метод итераций.
С помощью принципа максимума сравнительно просто оценивается характер оптимального по быстродействию управления. Для этого в соответствии с уравнением

составляется функция Гамильтона H₁(у, ψ, u). Затем определяется управление, при котором обеспечивается ее максимум:

Далее находится, сколько раз изменялся знак управления.
Пример 6.3. ОУ описывается дифференциальным уравнением второго порядка
T₁T₂ + (T₁+T₂) + y = Ku. (6.48)
Необходимо найти алгоритм управления, переводящий объект из положения. y(t₀) = 0, (t₀) = 0 в положение у(Т) = у_n, (Т) = 0 за минимальное время при ограничении |u| ≤ u_max.
Решение. Уравнение (6.48) представляется в виде системы двух уравнений:
Т_{1 2} + у₂ = Кu;
T₂ 1 = y₂.

Полученна система приводится к нормальному виду:

На основании уравнений (6.49) составляется сопряженная система уравнений для вспомагательных переменных ψ₁ и ψ₂:

Находятся решения для ψ₁ и ψ₂:

Записывается функция Гамильтона

и находится ее максимальное значение

Определяется закон уравнения ,

где

6.4 Динамическое программирование

В течение 50-х годов нашего столетия американский ученый Р. Беллман и ряд его сотрудников развили новый общий метод решения вариационных задач, названный ими динамическим программированием. В основу этого метода положен следующий принцип оптимальности: любой конечный участок оптимальной траектории является тоже оптимальной траекторией, т.е. часть оптимальной траектории от любой промежуточной точки до ее конца является оптимальной траекторией между этими точками, если считать данную промежуточную точку началом траектории (рис. 6.12).

Рис. 6.12 - К принципу оптимальности

Принцип оптимальности означает, что если траектория 1-2 между точками 0 и К является оптимальной, то оптимальным будет и любой ее конечный участок от произвольной точки i до точки К.
Этот принцип оптимальности не является всеобщим. Он справедлив для систем, у которых оптимальная траектория не зависит от предыстории системы, а целиком определяется исходным ее состоянием. В данном случае справедливость принципа оптимальности очевидна: если траектория 1-2 оптимальна, обеспечивая минимум критерия, то оптимальна и траектория 2, так как если оптимальной траекторией между точками i и К оказалась бы какая-то другая траектория 2', оптимальной траекторией между точками 0 и K была бы траектория 1-2', поскольку на ней критерий оптимальности имел бы меньшее значение, чем на траектории 1-2, за счет меньшего приращения его на участке 1 -2'.
Сформулированный принцип оптимальности является весьма общим необходимым условием оптимального процесса, справедливым как для непрерывных, так и для дискретных систем. Однако суть метода динамического программирования проще понимается на примере дискретной системы. Рассмотрим следующий простой пример (рис. 6.13).

Рис. 6.13 - К методу динамического программирования

Требуется перевести некоторый объект из точки 0 в точку К за (m+1) шагов, из которых m шагов имеют l вариантов, обеспечив при этом минимум критерия оптимальности I. Этот критерий оптимальности зависит от траектории движения, и известна величина его приращения ∆I, соответствующая шагу из любой точки пути (переходу из каждой точки вертикали, соответствующей началу очередного шага, в каждую точку на следующей вертикали, соответствующую концу этого шага). Таким образом, требуется выбрать оптимальную траекторию из точки 0 в точку К из конечного числа возможных траекторий, минимизирующую критерий I. Речь может идти, например, о выборе маршрута автомобиля, проходящего через заданные пункты и обеспечивающего минимум расхода горючего или времени движения. В данном случае величина I является функцией ml переменных. Число возможных их комбинаций, т.е. число возможных вариантов решения, равно l^m. При небольших значениях m и l оптимальное решение можно найти перебором возможных вариантов на ЭВМ, однако в большинстве реальных задач это потребовало бы чрезвычайно большого объема вычислений. Решение этой задачи методом динамического программирования резко сокращает объем работы.
Нахождение оптимальной траектории динамическим программированием начнем, пользуясь принципом оптимальности, с конечной точки К, "пятясь" к начальной точке 0. Результаты можно представить в виде таблицы (рис.6. 14). Для каждой исходной точки предпоследнего m-гo шага найдем, например перебором из l вариантов или любым другим методом нахождения оптимума функции, оптимальную траекторию перехода в точку К, дающую минимальное приращение ∆I критерия оптимальности.

Рис. 6.14 - Расчет приращения ∆I для нахождения оптиальной траектории

Затем, переходя к l исходным точкам предыдущего (m-1)-гo шага, находим для каждой из них оптимальную траекторию в конечную точку К и составляем таблицу (рис. 6.14) соответствующих значений ∆I_min. При этом суммарное значение ∆I_min для последних двух шагов берется из таблицы (рис.6.14). Аналогично находим оптимальную траекторию и значения ∆I_min с начала (m-2)-го шага и т.д., пока не дойдем до начальной точки 0. Последнее дает решение всей задачи, т.е. оптимальную траекторию в целом. Это решение, соответствующее минимальному значению критерия оптимальности I_min, определяется минимальной суммой из l сумм значений ∆I за первый шаг и найденных перед этим значений ∆I_min за последующие m шагов. Таким образом, в данном случае задача нахождения оптимального значения функции I m переменных, каждая из которых может иметь l значений, свелась к последовательному решению более простой задачи нахождения оптимума функции одной переменной, имеющей l значений, т.е. с помощью динамического программирования выбор из l^m вариантов сведен к многократному последовательному выбору всего из l вариантов. Например, для m = l = 10 выбор из 10¹⁰вариантов сводится к последовательному выбору из 10 вариантов.
Решение задачи описанным методом не обязательно требует движения от конца к началу. Можно, например, применить такую процедуру расчета. Вначале для каждой из точек конца второго шага (см.рис.6.13) находим оптимальную траекторию (оптимальную промежуточную точку в конце первого шага), дающую минимум ∆I. Затем то же определяем для каждой точки конца третьего шага, используя при этом ранее найденные оптимальные решения для суммы первых двух шагов. И так действуя далее, доходим до конечной точки К. При этом в конце предпоследнего шага для каждой из l точек оказываются найденными оптимальные траектории от начальной точки 0 и соответствующие значения минимального ∆I. Минимальная из сумм каждого из этих приращений с соответствующим данной точке ∆I на последнем шаге и определяет искомую оптимальную траекторию из начальной точки 0 в конечную точку К .
Математическая интерпретация метода. Предположим, что речь идет о цифровой САУ с квантованием по уровню и по времени, т.е. шаги в решении представляют собой фиксированные интервалы времени. Требуется найти закон управления объекта u(t) с учетом ряда ограничений, переводящий объект из состояния, характеризуемого точкой у(0) фазового пространства, в состояние, характеризуемое точкой у(Т), при условии обеспечения минимума критерия оптимальности в виде функционала:
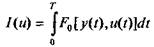(6.50)
Для дискретной системы с квантованием по времени интеграл в (6.50) заменяется суммой функций дискретных величин:
(6.51)
Здесь введено относительное время, так что n - это текущий номер периода квантования (см.рис.5.2, а, г). При этом соответственно уравнение объекта записывается в конечных разностях. Задача заключается в определении управляющего воздействия u[n], т.е. последовательности его дискретных значений u[0], u[1], ..., u[m-1], минимизирующих сумму (6.51) при заданных уравнениях объекта и ограничениях величин u и у на его входе и выходе. Допустим для простоты, что время процесса Т фиксировано, и будем искать решение, например, опять двигаясь "попятно" с конечного момента t=T, т.е. в относительном времени с момента n=m. Решение задачи начинаем с нахождения и запоминания оптимального значения управляющего воздействия u[m-1] в начале последнего интервала для каждого возможного дискретного значения у[m-1] (в пределах заданных ограничений последнего) и соответствующих значений приращения ∆I_m-1 критерия оптимальности. В результате находим оптимальные значения ∆I_m-1, и u[m-1] как функции у[m-1]. Затем переходим к началу (m-2)-го шага и также находим минимум ∆I_m-2 и соответствующее оптимальное значение u[m-2] как функцию выходной величины у[m-2] в этот момент. Минимальное значение ∆I_m-2 для конкретного значения у[m-2] определяем варьированием u[m-2]. При этом для каждого значения u[m-2] сперва находим приращение критерия оптимальности за второй шаг и значение y[m-l] в конце второго шага. После этого определяем полное ∆I_m-2 за два шага, используя ранее найденную зависимость ∆I_m-1 от y[m-l]. Переходя далее к началу (m-З)-го шага и т.д., попадем, в конце концов, в начальную точку y[0], определив при этом закон оптимального управления u[n], сам оптимальный процесс у[n] и суммарную величину критерия оптимальности I. Таким образом, оптимизация функционала, зависящего от искомой функции u[n], заменяется последовательностью т оптимизаций значительно более простой функции ∆I_m-i одной переменной u[m-i]. Благодаря последнему упрощению метод динамического программирования позволяет решать задачи оптимизации, не решаемые классическими методами вариационного исчисления путем прямой оптимизации исходного функционала.
Описанную процедуру решения лишь в простейших случаях можно довести до получения аналитического выражения искомого решения. В общем же случае метод динамического программирования в изложенной выше трактовке следует рассматривать как метод составления программы для численного решения вариационной задачи на ЭВМ.
Изложим метод динамического программирования для непрерывных систем на примере синтеза оптимального управления ОУ с ограниченными координатами. Требуется перевести изображающую точку ОУ в пространстве состояний из состояния y(0) в некоторую область пространства состояний (фазового пространства) за определенное время Т, минимизируя функционал (6.50). Условия, которым должны удовлетворять фазовые координаты объекта и управляющие воздействия на него, в векторной форме могут быть записаны в виде:
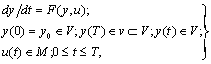(6.52)
где V - область фазового пространства, из которой не должна выходить экстремаль y(t);
М - замкнутое ограниченное множество функций, из которого выбираются кусочно-непрерывные управления u(t);
у, F- n-мерные векторы; и, F₀ - скалярные функции.
Если за начало отсчета взять не t=0, а некоторую другую точку t₁, интервала [0,T], а в качестве начальных условий выбрать новую точку y(t₁) из области V и найти оптимальное управление, минимизирующее функционал
(6.53)
то значение минимума функционала (6.53) будет отличаться от минимума функционала (6.50) при условиях (6.52). Следовательно, минимум функционала есть функция от начального момента времени t₁ и начальной точки y(t₁) которую обозначим через S[t₁, y(t₁)] - Если эта функция определена при t=0, y(0) = у₀, то S[0, у₀] есть минимум функционала (6.50).
Обозначив через у(0, у₀) оптимальную траекторию в фазовом пространстве, на которой реализуется минимум функционала (6.50) при условиях (6.52), а через y(t₁, 0, y₀) - точку, соответствующую новому началу отсчета t₁ и расположенную на оптимальной траектории у(0, у₀), можно записать еще одну формулировку принципа оптимальности: если принять значения t₁, y(t₁) за начальные, то на интервале [t₁,T] оптимальное управление u[t₁, y(t₁)], на котором реализуется минимум функционала (6.53), совпадает с оптимальным управлением u(0, у₀), и, следовательно, участок оптимальной траектории у(0, у₀) для задачи с начальными значениями t=0, y(0)=0 на интервале [t₁,T] совпадает с оптимальной траекторией для задачи с начальными значениями t₁, y(t₁).
Если известна функция S(t, у), где t - произвольная точка на интервале [0,Т], а у - произвольная точка из области V , то с помощью условий (6.52) нетрудно найти оптимальное управление. Однако сложно определить S(t,y) в аналитической форме, поэтому чаще всего эту функцию определяют приближенно. Основой приближенного метода определения S(t, у) служат следующие положения. Выражение для S[t₁, y(t₁)] можно записать следующим образом:
(6.54)
где t₁ - фиксированный момент времени на интервале [0, T];
∆t - малое положительное число.
Функции y(t), u(t) связаны условиями:
(6.55)
В силу принципа оптимальности поведение u(t) на интервале [t₁ + ∆t,Т] не влияет на величину первого интеграла в выражении (6.54), поэтому u(t) на этом интервале выбирается так, чтобы минимизировать второй интеграл. Тогда выражение (6.54) можно записать в виде
(6.56)
Из формулы (6.56) следует, что управление u(t) на интервале [t₁, t₁+∆t] нужно выбрать так, чтобы минимизировать выражение в фигурных скобках. Поведение u(t) на интервале [t₁, t₁+∆t] влияет не только на величину интервала в выражении (6.56), но и на величину S[t₁ + ∆t,y(t₁+∆t), так как аргумент этой функции y(t₁, ∆t), в свою очередь, является функцией u(t₁) и y(t₁) в силу уравнения (6.55, а).
Трудности нахождения минимума (6.56) облегчаются, если предположить, что функции u(t) и y(t) за время ∆t изменяются мало и их можно считать постоянными. Это допущение позволяет заменить вектор-функцию F(y,u) (6.55, а) и подынтегральную функцию F₀(y,u) их значениями в точке t₁, а производную dy(t)/dt - конечной разностью При таких допущениях получим:
(6.57)
(6.58)
Определение S[t₁, y(t₁)] производится методом попятного движения, т.е. начиная с момента времени t₁ = Т - ∆t.
Первый шаг. Подставляя в (6.57) и (6.58) t₁ = Т - ∆t и учитывая, что S[T, у(Т)]=0 при у(Т) ∈ v , получим
S[T - ∆t,y(T-∆t)] = F₀[y(T - ∆t), u(T - ∆t)]∆t; (6.59)
y(T - ∆t) + ∆y(T - ∆t) = у(Т - ∆t) + ∆yF[y(T - ∆t),u (T - ∆t)]. (6.60)
Минимум правой части (6.59) вычисляется для значений u(T - ∆t) из М и [у(Т - ∆t) + ∆у(Т - ∆t)] из v, т.е. для значений, удовлетворяющих ограничениям на эти функции. Чаще всего S[T-∆t,y(T-∆t)] получается в виде набора дискретных значений, соответствующих различным значениям y(T - ∆t), с которыми связаны определенные значения u[(T - ∆t, y(T - ∆t)].
Второй шаг. Фиксируется момент времени t = T - 2∆t. С помощью тех же действий, что и на первом шаге, получаются выражения:
S[T - 2∆t, y(T - 2∆t)] = {F₀[y(T - 2∆t), u(T - 2∆t)] + S[T - ∆t, y(T - ∆t)]}; (6.61)
y(T - 2∆t) + ∆y(T - 2∆t) = у(Т - 2∆t) + ∆tF[y(T - 2∆t), u(T - 2∆t)]. (6.62)
Зависимости (6.61) и (6.62) после подстановки в них результатов, полученных на первом шаге, позволяют определить функцию S[T - 2∆t, y(t - 2∆t)] и управление y[T-2∆t,y(T-2∆t)]. Далее процедура повторяется, при этом для вычислений могут быть использованы рекуррентные формулы:
S[T - k∆t,y(T - k∆t)] = {F0[y(T - k∆t), u(T - k∆t)] + S[T - (k-1)∆t, y(T - (k-1)∆t)]};
y(T-k∆t) + ∆y(T - k∆t) = у(Т k∆t) + ∆tF[y(T - k∆t), u(T - k∆t)],
где k - номер шага.
Вычисления продолжаются до тех пор, пока не будет получена функция S[0,y(0)], где у(0) - произвольная точка из множества V_m. Если заданная начальная точка y(0)=y₀ из условий (6.52) принадлежит множеству V_m, то, полагая в функции S[0,y(0)] y(0)=y₀, получим S[0,y₀] - минимум функционала (6.50) и u[0,y] - оптимальное управление.
Если функция S[t, y(t)] имеет непрерывные частные производные по всем своим аргументам, то она может быть найдена из следующего уравнения:

при условиях (6.52) и S[T,y(T)]=0. Уравнение (6.63) принято называть уравнением Беллмана.
Существование непрерывно дифференцируемой функции S(t,y) - решения уравнения (6.63) - является достаточным условием оптимальности. Если существует решение уравнения (6.63), то соответствующее ему управление u(t, у) будет реализовывать минимум критерия оптимальности (6.50). Требование непрерывной дифференцируемости функции S(t,y) серьезно ограничивает использование уравнения (6.63) для синтеза оптимальных систем, так как оно не выполняется во многих даже простых задачах. Однако В. Г. Болтянским показано, что возможно использование уравнения Беллмана и в случае, когда частные производные от функции S(t,y) терпят разрывы на некотором множестве N.
Уравнение (6.63) представляет собой нелинейное дифференциальное уравнение в частных производных, и в настоящее время нет общего метода, позволяющего определить S(t,y) и u(t, у) в явно аналитической форме. Каждая новая задача требует особого исследования.
Решение задач синтеза оптимальных САУ с помощью динамического программирования численными методами требует такого объема вычислительной работы, которая непосильна даже для современных ЭВМ. Но метод динамического программирования обладает рядом достоинств:
- в процессе решения задачи оптимальное управление определяется как функция фазовых координат ОУ, что упрощает синтез замкнутых оптимальных САУ;
- метод без принципиальных изменений применим для синтеза как равномерно-оптимальных, так и статистически-оптимальных систем;
- принципу оптимальности Беллмана удовлетворяют только те оптимизирующие функции S(t, у), которые одновременно являются функциями Ляпунова для замкнутой системы. Следовательно, соответствующие этим функциям управления u(t, у) и формирующие их УУ не только обеспечивают минимум критерия качества, но и устойчивость замкнутых систем;
- метод позволяет получать физически понятные алгоритмы решения задач оптимального управления на ЭВМ.
Достоинства и перспективность метода динамического программирования стимулируют проведение исследований по его совершенствованию. В настоящее время появляется много работ, направленных на уменьшение требуемого объема памяти ЭВМ при решении задач динамического программирования численными методами и на разработку методов синтеза различных типов оптимальных САУ с использованием уравнения Беллмана.
Приведем два примера решения задач оптимального управления с помощью уравнения Беллмана.
Пример 6.4. Пусть возмущенное движение ОУ описывается системой (6.36). Естественные граничные условия заданы в том же виде, что и в примере 6.2. Требуется определить управление, минимизирующее критерий качества
(6.64)
a_j > 0 (j=1,2,…,n), c>0.
На величину управления u(t) ограничений не накладывается, однако критерий качества пропорционален расходу энергии УУ.
Решение. Для рассматриваемого случая уравнение Беллмана имеет вид
(6.65)
Выражение в квадратных скобках является квадратным трехчленом относительно управления, на величину и ограничений не накладывается и c>0, поэтому минимум в уравнении (6.65) достигается при том значении и, при котором производная от выражения в квадратных скобках по аргументу и обращается в нуль:
(6.66)
После подстановки выражения (6.66) в уравнение (6.65) получается нелинейное уравнение в частных производных относительно функции S:
(6.67)
Решение этого уравнения ищем в виде
(6.68)
где A_kj - неизвестные коэффициенты, подлежащие определению.
Функция (6.68) удовлетворяет граничному условию, так как при у_j=0 (j=1,2,...,n) функция S=0. Путем подстановки

в уравнение (6.67) получается
(6.69)
Левая часть уравнения (6.69) тождественно обращается в нуль как квадратичная форма переменных у_j(j=1,2,...,n) только в случае равенства нулю всех ее коэффициентов. На основании этого вывода и второго равенства (6.68) записывается система алгебраических уравнений:

 

Путем замены (6.66) и подстановки u (6.66} в систему уравнений (6.36) находим

После определения коэффициентов A_ji так, что бы удовлетворялась система уравнений (6.70) и обеспечивалась асимптотическая устойчивость системы (6.71), алгоритм УУ записывается в виде:

Рассмотренная задача решена A.M. Летовым.
В соответствии с изложенной общей методикой решения задачи ниже приводится пример определения алгоритма УУ в системе, ОУ которой описывается дифференциальным уравнением:

Минимизируемый критерий качества имеет вид :

Уравнение Бвллмана и условие минимума его левой части о управлению и имеют следующий вид:

С учетом вьражений (6.73) и (6.74) получаем:

Из уравнения (6.76) следует:

После подстановки выражения (6.77) в уравнение (6.75} получим:

Решение уравнения (6.78) ищем в форме (6.68):

После подстановки выражения (6.80) в уравнение (6.78) получим:

Из этого следует:

Из двух значений А₁₁ необходимо выбрать положительное(из условия устойчивости системы), т.е.

Согласно (6.77) алгоритм УУ запишется в виде :

Пример 6.5. Решим задачу определения оптимальной диаграммы тока двигателя постоянного тока, т.е. определим закон изменения тока якоря при отработке за минимальное время пемещения
Нагрев обмотки якоря двигателя не должен превышать величины

Критерий оптимальности (621): . Решение. Если положить R = 1 Ом и обозначить y₁= ω , у₁, = φ , , то система уравнений ОУ примет вид:

Уравнение Беллмана и условие минимума его левой части по управлению u образуют систему:

Ток якоря определяется из уравнения (6.82):

После подстановки выражения (6.83) в формулу (6.81) получим:

В этом случае решение уравнения (6.84) не будет квадратичной формой координат y₁, y₂, y₃, так как критерий оптимальности выбран неквадратичный. Решение можно записать в виде

Из равенства (6.85} определим частные производные:

После подстановки в уравнение (6.84) находим уравнения, из которых определяются а_i :

Если положить a₃ = 1, то остальные коэффициенты примут
значение a₁=a₂ = 4/3 .
Тогда алгоритм УУ можно записать в виде

Контрольные вопросы

1. Понятие об оптимальном управлении.
2. Основные задачи синтеза оптимальных САУ и их особенности.
3. Классификация оптимальных САУ.
4. Основные методы теории оптимального управления.
5. Вариационное исчисление. Основные понятия и определения.
6. Необходимые условия экстремума функционала. Уравнения Эйлера-Лагранжа. Условия Вейерштрасса-Эрдмана.
7. Постановка задач синтеза САУ:
- оптимальных по быстродействию;
- оптимальных по расходу ресурсов;
- с минимальной энергией управления;
- с минимальными потерями управления.
8. Решение задач синтеза оптимальных САУ.
9. Теорема об п -интервалах.
10. Пример синтеза САУ оптимальной по быстродействию.
11. Задача аналитического конструирования регуляторов (пример).
12. Геометрическая интерпретация принципа максимума Понтрягина.
13. Функция Гамильтона для автономной системы.
14. Основная теорема принципа максимума.
15. Функция Гамильтона для неавтономной системы.
16. Определение оптимальных по быстродействию управлений с помощью принципа максимума.
17. Геометрическая интерпретация принципа оптимальности Беллмана.
18. Решение дискретной задачи определения оптимальной траектории методом динамического программирования.
19. Синтез оптимальных дискретных САУ методом динамического программирования.
20. Формулировка принципа оптимальности Беллмана для непрерывных динамических систем.
21. Вывод уравнения Беллмана.
22. Достоинства метода динамического программирования.
23. Синтез САУ, оптимальной по расходу энергии
управления методом динамического программирования (решение A.M. Летова).
24. Синтез алгоритма УУ САУ, оптимальной по расходу энергии управления (частный случай).
25. Синтез оптимального алгоритма управления двигателем постоянного тока методом динамического программирования (пример).

 

---

Дата добавления: 2021-04-15; просмотров: 694; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!