ЭЛЕМЕНТЫ ТЕОРИИ НЕЛИНЕЙНЫХ САУ

Основы Теории Управления

Содержание

Предисловие

4 ЭЛЕМЕНТЫ ТЕОРИИ НЕЛИНЕЙНЫХ САУ
4.1 Основные свойства и виды нелинейных систем
4.2 Линеаризация непрерывных гладких нелинейных характеристик
4.3 Устойчивость нелинейных систем
4.3.1 Устойчивость в малом (устойчивость по Ляпунову)
4.3.2 Первый метод Ляпунова
4.3.3 Второй (прямой) метод Ляпунова
4.3.4 Проблема Айзермана. Критерий абсолютной устойчивости В.М. Попова
4.4 Исследование нелинейных систем методом точечных преобразований
4.5 Гармоническая линеаризация
4.5.1 Гармонические коэффициенты усиления некоторых типовых нелинейных звеньев
4.5.2 Приближенное исследование стационарных нелинейных систем
4.6 Качество переходных процессов и коррекция нелинейных САУ

Контрольные вопросы

5. ДИСКРЕТНЫЕ СИСТЕМЫ.СИСТЕМЫ УПРАВЛЕНИЯ С ЭВМ
5.1 Понятие о дискретном управлении
5.2 Математическое описание дискретных систем
5.2.1 Характеристики дискретных (импульсных) линейных САУ
5.2.2 Передаточная функция стационарной дискретной импульсной линейной системы с дискретным выходом
5.2.3 Передаточная функция стационарной дискретной импульсной линейной системы с непрерывным выходом
5.2.4 Описание дискретных систем разностными уравнениями
5.2.5 Описание дискретных систем в пространстве состояний
5.2.6 Преобразование моделей дискретных систем в пространстве состояний
5.2.7 Преобразование уравнений состояния в модели типа "вход - выход"
5.3 Устойчивость дискретных систем
5.3.1 Устойчивость дискретных линейных систем
5.3.2 Устойчивость дискретных систем в пространстве состояний
5.3.3 Второй метод Ляпунова
5.4 Управляемость и наблюдаемость дискретной САУ
5.4.1 Декомпозиция Калмана
5.4.2 Потеря достижимости и наблюдаемости при квантовании
5.5 Графовые модели дискретной нелинейной динамической системы

Контрольные вопросы

6. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
6.1 Общие сведения об оптимальном управлении и задачи синтеза оптимальных САУ
6.2 Вариационное исчисление и его использование в теории оптимальных САУ
6.2.1 Системы, оптимальные по быстродействию
6.2.2 Системы, оптимальные по расходу ресурсов
6.2.3 Системы с минимальной энергией управления
6.2.4 Системы с минимальными потерями управления
6.3 Принцип максимума
6.3.1 Управление автономной системой
6.3.2 Основная теорема (принцип максимума)
6.3.3 Управление неавтономной системой
6.3.4 Определение оптимальных по быстродействию управлений с помощью принципа максимума
6.4 Динамическое программирование

Контрольные вопросы

7. АДАПТИВНОЕ И ИНТЕЛЛЕКТУАЛЬНОЕ УПРАВЛЕНИЕ
7.1 Общие сведения об адаптации и интеллектуальности в САУ
7.1.1 Условия оптимальности
7.1.2 Итеративные алгоритмы оптимизации
7.1.3 Вероятностные итеративные алгоритмы
7.2 Адаптивное управление
7.2.1 Дуальное управление
7.2.2 Поисковые адаптивные САУ
7.2.3 Беспоисковые адаптивные САУ
7.2.4 Модель чувствительности
7.3 Интеллектуальное управление

Контрольные вопросы

Заключение

Литература

Литературный комментарий

 

Предисловие

 

Учебное пособие написано для студентов, обучающихся по специальности "Автоматизация и управление", но может быть полезно широкому кругу читателей, особенно студентам и аспирантам технических специальностей, а также инженерам, желающим повысить свою квалификацию в области теории управления.
Учебное пособие состоит из двух частей. Первая часть содержит три раздела. В 1-м разделе изложены этапы становления и развития теории регулирования и управления, основные понятия и определения теории управления, функциональные типовые схемы систем автоматического управления (САУ), принципы управления и классификация САУ. Математическому описанию непрерывных линейных САУ посвящен 2-й раздел. Здесь представлены основные характеристики непрерывных линейных САУ, характеристики стационарных САУ, описываемых линейными дифференциальными уравнениями, и их соединений, линейные законы регулирования. В 3-м разделе описаны процесс управления и требования к нему, изложены основы теории устойчивости и качества процессов управления в непрерывных линейных САУ, освещены вопросы коррекции динамических свойств САУ, представлены элементы теории инвариантности и ковариантности.
Настоящая вторая часть учебного пособия состоит из 4-х разделов, в которых последовательно изложены элементы теории нелинейных САУ, дискретных САУ и САУ с ЭВМ, оптимального, адаптивного и интеллектуального управления. Центральную идею 2-й части учебного пособия удачно выразил К.Л. Зигель: "По Лейбницу наш мир является наилучшим из всех возможных миров и поэтому законы природы можно описать экстремальными принципами". Эти принципы являются базовыми для современной теории управления. Ограничения по объему часов, выделяемых для данной дисциплины, и соответствующие ограничения по объему учебного пособия не позволяют представить теорию управления во всей полноте. Автор надеется, что эта книга вместе с литературным комментарием и списком литературы убедит читателя в том, что теория управления выделяется среди других наук особым разнообразием идей и методов и продолжает интенсивно развиваться благодаря сотрудничеству с математикой и применению вычислительной техники.

ЭЛЕМЕНТЫ ТЕОРИИ НЕЛИНЕЙНЫХ САУ

 

4.1 Основные свойства и виды нелинейных систем

 

Согласно определению, данному в подразделе 1.4, нелинейной системой называется любая система, для которой не выполняется принцип суперпозиции (1.1). Система является нелинейной при наличии в ней хотя бы одного звена (элемента), для которого не выполняется этот принцип. На практике разнообразные по физическим свойствам системы в своем большинстве являются нелинейными, так как во всякой системе присутствует, как правило, одна или несколько нелинейностей.
Процессы, протекающие в нелинейных системах, гораздо разнообразнее и сложнее процессов в линейных системах.
Перечислим некоторые особенности поведения нелинейных систем.
1. Выходной сигнал неустойчивой линейной системы неограниченно растет, когда время стремится к бесконечности, а в нелинейной системе выходная реакция может стремиться к бесконечности на конечном интервале времени.
Например, выходной сигнал системы, описываемой уравнением 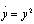с начальным условием y(0) = у₀, будет стремиться к бесконечности при t = 1/у₀.
2. Выходной сигнал устойчивой линейной системы при отсутствии входного воздействия стремится к нулю. Это совсем необязательно для нелинейных систем. Например, триггер, имея два устойчивых состояния, может находиться в одном из них независимо от начальных условий. Известны примеры систем, имеющих целую зону равновесных состояний, и при этом система может находиться в любом из них.
3. Для существования в стационарной линейной системе незатухающих колебаний необходимо, чтобы пара полюсов ее передаточной функции располагалась на мнимой оси. В этом случае амплитуда колебаний определяется начальными условиями. В нелинейных системах возможны устойчивые колебания определенной амплитуды и частоты независимо от начальных условий. Такие колебания характеризуют предельный цикл и называются автоколебаниями.
4. В устойчивой линейной системе синусоидальный входной сигнал определяет выходной сигнал той же частоты. Поведение нелинейной системы при синусоидальном входном сигнале совершенно иное. На выходе нелинейного звена могут присутствовать дополнительные гармоники, поэтому частота выходного сигнала кратна частоте входного. Иногда в таких системах возникают субгармонические колебания с периодом выходного сигнала, кратным периоду входного, т.е. частота сигнала на выходе во много раз ниже частоты сигнала на входе. В некоторых нелинейных системах синусоидальный сигнал на входе вызывает почти периодические движения.
5. В некоторых нелинейных системах при отсутствии входного воздействия выходной сигнал, в зависимости от начальных условий, стремится к одному или нескольким устойчивым состояниям, или к одному или нескольким предельным циклам. Для систем, на входе которых действует гармонический сигнал, на выходе могут быть гармонические, субгармонические либо почти периодические колебания в зависимости от амплитуды и частоты входного сигнала, а также другие явления.
6. В некоторых нелинейных системах возникает явление скачкообразного резонанса, когда амплитуда и частота периодического входного сигнала плавно изменяются, а на выходе наблюдается скачок амплитуды. Резонанс в нелинейной системе возможен на дробной частоте, т.е. на частоте, равной некоторой доле частоты входного воздействия.
7. В нелинейных системах случается явление захвата частоты (синхронизация): система управляется синусоидальным входным сигналом малой амплитуды и на выходе возникают колебания кратной частоты, при увеличении входного сигнала существует момент, когда частота выходного сигнала скачком уменьшается до частоты входного.
8. В нелинейных системах может наблюдаться скачкообразный резонанс как амплитуды, так и частоты выходного сигнала. Некоторым нелинейным системам свойственны явления параметрического возбуждения и резонанса, заключающиеся в том, что в системе возникают колебания при периодическом изменении какого-либо ее параметра.
Особые свойства нелинейных систем широко используются в ТАУ, на этой основе созданы нелинейные САУ, в которых рационально используются нелинейные характеристики отдельных звеньев (элементов). По динамическим качествам нелинейные САУ во многих случаях превосходят линейные САУ.
Однако часто нелинейности характеристик элементов САУ являются вредными факторами. Их надо либо устранять, либо выбирать режим работы САУ таким, чтобы нелинейности не оказывали существенного влияния на процессы управления в САУ.

Особенности поведения нелинейных систем создают трудности их точного математического описания и теоретического изучения. Проведем на примерах классификацию основных типов нелинейностей.
1. Нелинейности релейного типа. Обозначим функциональную зависимость нелинейности
y = F(х), (4.1)
где у и х - соответственно выходная и входная величина нелинейного звена.
В общем случае звено типа (4.1) имеет характеристику вида 2 (рис. 1.11, б) с зоной нечувствительности и гистерезисной петлей, т.е. петлей, выражающей нелинейное (координатное) запаздывание при срабатывании реле из-за того, что ток отпускания хср меньше тока срабатывания хср. Известны различные частные случаи рассматриваемой нелинейности : имеется только зона нечувствительности без петли; есть только петля гисте-резисного типа без зоны нечувствительности; иногда учитывается запаздывание по времени срабатывания реле. Наконец, можно рассматривать идеальную релейную характеристику вида 1 (рис. 1.11,6), когда
y = F(x) = y_cpsignx, (4.2)
где sign(x) - знаковая функция, определенная формулой (3.40).
Возможна идеальная релейная характеристика со средним положением (трехпозиционная)

Нелинейности релейного типа могут быть и несимметричными, например, если реле или контактная пара работает в режиме включения и выключения напряжения одной полярности.
2. Нелинейности непрерывных статических характеристик звеньев. Они записываются также в форме (4.1) и могут задаваться аналитически в виде степенных и других функций или же графически. F(x) может иметь зону нечувствительности (рис. 1.11, в - ломаная линия 1), гистерезисную петлю (рис. 1.11, а - кривая 3), а также может быть несимметричной (рис. 1.11, а -кривые 1 и 2).

Особый вид имеет характеристика зазора в механической зубчатой передаче (рис. 4.1), называемая также мертвым ходом (люфтом). Причиной люфта является неточное изготовление и одностороннее соприкосновение зубьев шестерен, поэтому при перемене направления движения ведомая деталь (шестерня) остается неподвижной, пока не будет выбран зазор (горизонтальные стрелки на рис. 4.1).

Рис. 4.1 - Люфт

 

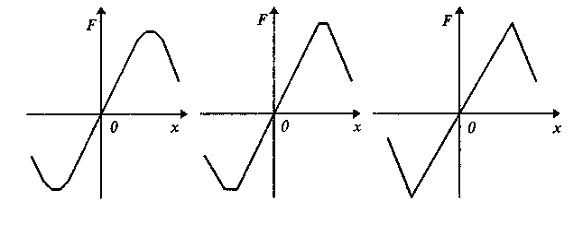
Рис. 4.2 - Периодитечские нелинейности

Некоторые САУ содержат звенья с периодическими нелинейностями (рис. 4.2), которые отличаются наличием участков с отрицательным наклоном.
3. Динамические нелинейности описываются нелинейными дифференциальными зависимостями.
Примером динамической нелинейности может служить звено с нелинейным трением и нелинейной восстанавливающей силой:
mp²у + F₁(ру) + F(y) = kx, (4.4)
причем нелинейности F₁ и F могут быть различного типа, на
пример нелинейное трение F₁ может быть квадратичным
F₁(py) = с(ру)²signру или вида F₁(py) = k₁py + c(py)²signpy.
Приведем еще один пример динамической нелинейности: сухое трение (рис. 4.3) Эта нелинейность имеет важную особенность, состоящую в том, что при ру = 0 сила трения F1 может принимать любое значение в пределах
-c≤F₁≤c, (4.5)
равное в каждый момент времени сумме всех действующих сил,
включая силу инерции. Поэтому система остановится в момент
времени, когда ру = 0 и |F₁|< с. Застой будет до тех пор, пока
изменение сил не приведет к значению |F₁| = с, после чего снова
начнется движение системы. Заметим, что в этом случае характеристика сухого трения (рис. 4.3, а, б) принципиально отлична
от релейной (рис. 1.8, б - кривая 1), имеющей внешне аналогичный вид. Если же в процессе движения системы всегда оказывается при ру = 0 |F₁| ≥с, то застоев не будет, и характеристика
трения (рис. 4.3, а, б) не будет отличаться от релейной.

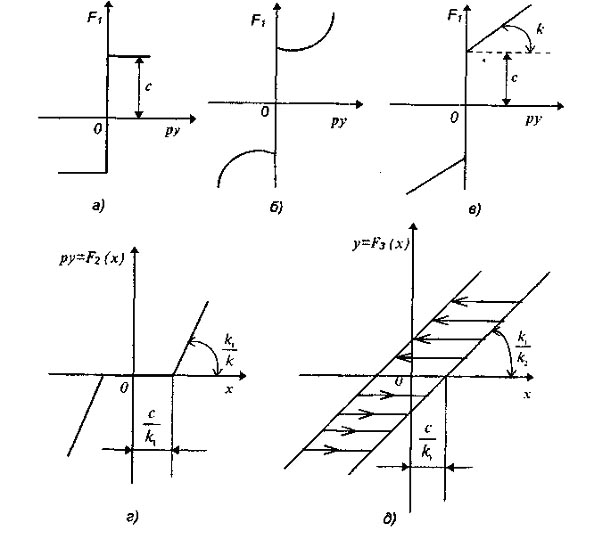
Рис. 4.3 - Сухое трение

При наличии линейного и сухого трения (рис. 4.3, в), а также линейной восстанавливающей силы уравнение (4.4) запишется в следующем виде:
mр²у + kpy + csign py + k₂у=k₁х , (4.6)
если только
|k₁x-k₂y-mр²у|≤с при py = 0. (4.7)
Если же в процессе движения в момент выполнения равенства ру=0 окажется, что
|k₁x-k₂y-mp²y| <c,
то уравнение (4.6) будет справедливо только при ру≠0 , а при ру=0 начнется застой согласно (4.5), который будет продолжаться до тех пор, пока правая часть k₁x изменяется в пределах

(k₂y_m-c)<k₁x<(k₂y_m+c) при py=0 (4.8)
где ут - значение у, получившееся в момент остановки.
Кроме застоев, здесь могут быть скачки и срывы движения.
В случае чисто сухого трения (рис. 4.3, а) в уравнении (4.6) следует положить k = 0.
Из вышеизложенного следует, что математическая модель рассматриваемого нелинейного колебательного звена с сухим трением при наличии массы и восстанавливающей силы выглядит достаточно сложно для исследования известными методами.
Значительное упрощение произойдет в общем случае (4.6) при выполнении условия отсутствия застоев (4.7), т.е. когда характеристика сухого трения сводится к идеальной релейной, а также при наличии застоев в следующих двух частных случаях.
В первом частном случае массой из-за ее малости можно пренебречь и восстанавливающей силы нет, поэтому уравнение (4.6) при условии, что линейное и сухое трение описываются выражением (4.3), и с учетом (4.5) принимает следующий вид:

Эти уравнения эквивалентны нелинейной функции py = F₂(x) (рис. 4.3, г).
Следовательно, влияние сухого трения сводится к возникновению зоны нечувствительности для зависимости скорости на выходе звена от входной величины. Это обычно имеет место в приводных устройствах.
Во втором частном случае, когда величиной массы пренебрегается, но имеются чисто сухое трение (рис. 4.3, а) и линейная восстанавливающая сила, уравнение (4.6) примет с учетом (4.8) вид

Эти уравнения эквивалентны нелинейной функции y = F₃(x) (рис.4.3,д), где горизонтальные линии соответствуют различным значениям y_m.
Следовательно, влияние сухого трения оказалось эквивалентным зазору (люфту) в механической зубчатой передаче (рис. 4.1).
Итак, явление сухого трения, приводящее в общем случае к сложным движениям, трудно поддающимся анализу, в частных случаях может быть описано более простыми нелинейными характеристиками (идеальной релейной, зоны нечувствительности, зазора).
В дальнейшем эти частные случаи будут дополнительно исследованы.
В заключение отметим, что учет сил сухого трения в течение столетия был трудной проблемой ТАУ.
И.А. Вышнеградский пренебрег силами сухого трения, и в первые десятилетия 20-го века делались безуспешные попытки учесть их влияние, но математический аппарат не был подготовлен, поэтому исследователи получали весьма частные результаты либо сводили свое исследование к громоздким численным расчетам. Но вместе с тем эти работы имели огромное значение, так как предопределили новые математические направления теории управления.
4. Нелинейность переменной структуры является особым типом динамической нелинейности и связана с изменением структуры передаточных функций или структуры дифференциальных уравнений САУ.
К основной части САУ W₁(p) (рис. 4.4) добавляется одна из двух обратных связей W₁(p) или W₂(p) в зависимости от значения переменной х:

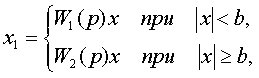
т.е. при достаточно малых значениях |х| < b включается обратная связь W₁(p), а при больших значениях |х|>b включается обратная связь W₂(p).

Рис. 4.4 - Нелинейная коррекция

Каждая из обратных связей W₁(р) и W₂(p) является линейной, но в целом получается нелинейное корректирующее устройство, так как переключение с одной связи на другую определяется значением самой переменной х.
5. Нелинейность логического типа. Логическое устройство может иметь два или несколько входов и выдавать ступенчатый сигнал в зависимости от определенных логических комбинаций свойств входных величин.
Приведем простой пример: на вход логического устройства подаются отклонение управляемой величины у и скорость отклонения х=ру, а выход логического устройства z = Ф(у,х) равен +1; -1; 0 в зависимости от сочетания значений у и ру.
Логика формирования выхода может быть самой разнообразной. Обычно ее изображают таблично или графически на фазовой плоскости у, х=ру.
Устройство (рис. 4.5) срабатывает при пороговых значениях у = у₀, х = х₀, и сигналы управления (Ф = + 1 или Ф=-1) подаются тогда, когда знаки у и ру одинаковы (система уходит из требуемого режима у = х = 0), а при противоположных знаках у и ру сигнал не подается (Ф = 0), так как система сама приближается к требуемому состоянию.

Рис 4.5 - Нелинейная логика

6. Нелинейности самонастройки и оптимизации. Во многих адаптивных системах используются нелинейности функционального типа (пп.2 или 3) и перемножение переменных.
При оптимизации САУ часто приходят к нелинейному управлению. Например, при использовании принципа максимума, который будет изложен далее, даже в САУ с неизменяемой линейной частью результат оптимизации по быстродействию для систем второго порядка определяет управление в следующем виде:

где принимает различные выражения для разных систем.
7. Нелинейные законы управления. В подразделе 2.4 были рассмотрены линейные законы управления, содержащие основной управляющий сигнал, интегралы от него и производные. В любой из этих элементов закона управления может быть введена любая из рассмотренных выше типов нелинейностей. Соответственно различают следующие три основные группы нелинейных законов управления: функциональные, логические, параметрические.
Функциональные нелинейные законы управления содержат какие-либо из нелинейностей, описанных в пп.1, 2, 3.
Логические нелинейные законы управления изложены в пп.4, 5, б, в этих законах могут содержаться некоторые из нелинейностей п.1 (например релейно-импульсные).
Параметрические нелинейные законы управления содержат нелинейные функции от параметров (переменных), входящих в математическое описание алгоритма (программы) управления.
С точки зрения математического описания и исследования нелинейных систем важным является то, что в задачах практики обычно всегда удается все нелинейные свойства системы отнести к безынерционным нелинейным звеньям и считать с достаточной точностью, что любая система состоит из ряда линейных звеньев и элементарных нелинейных безынерционных звеньев, соединенных различными связями.
Например, в нагревательных печах сначала имеем нелинейный процесс F , связанный с теплохимическими превращениями, а затем процесс распространения тепла, который можно описать в первом приближении линейными уравнениями, т.е. линейным звеном.
Следовательно, нагревательная печь как нелинейная система (рис. 4.6) может быть описана следующими соотношениями:

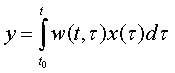- линейное звено,
х = F (u) - безынерционное нелинейное звено.

Рис. 4.6 - Пример структуры нелинейной системы

 

Подобные безынерционные нелинейности выполняют особую роль. Их принято называть элементарными безынерционными звеньями. Выходная переменная этого звена в каждый данный момент времени зависит только от значений входной переменной в тот же момент времени и не зависит от того, как изменялась входная переменная до данного момента времени. Таким образом, оператором элементарного безынерционного звена является обычная функциональная зависимость между входной и выходной переменными. Она называется характеристикой элементарного безынерционного звена.
Примеры характеристик элементарных безынерционных звеньев приведены выше, в пп.1 - 7 при классификации нели-нейностей.
Характеристики элементарных нелинейных звеньев делят на несущественные (слабые) нелинейности и существенные нелинейности.
К первой группе нелинейностей относятся такие, которые при малом диапазоне изменения входного сигнала или при малом его отклонении от изменяющегося среднего значения могут быть заменены линейными.
На рис. 1.8, в пунктирной линией 2 представлен пример типовой характеристики усилителя с насыщением. Насыщение наступает постепенно при больших х.
Наличие подобных нелинейностей мало сказывается на динамике системы: при малых значениях входных сигналов таких нелинейностей система ведет себя как линейная и только при больших входных сигналах проявляются ее нелинейные свойства, которые необходимо учитывать.
Ко второй группе относятся нелинейные характеристики, которые являются существенно нелинейными функциями, например разрывными или близкими к ним.
Зависимость между входной и выходной переменными для таких звеньев часто может быть приближенно представлена в виде кусочно-линейных функций. Примеры таких характеристик приведены на рис. 1.8, б, в (2), 4.1, 4.3.
В дальнейшем будем обозначать характеристику любого элементарного безынерционного нелинейного звена буквой F (формула(4.1)) и при этом всякий раз оговаривать однозначна или неоднозначна эта функция.

4.2 Линеаризация непрерывных гладких нелинейных характеристик

 

Существует большой класс нелинейных систем, содержащих так называемые слабые нелинейности, имеющих непрерывные гладкие характеристики, которые при определенных допущениях можно линеаризовать, т.е. систему сделать линейной в математическом смысле. К настоящему времени известно 4 способа (методики) составления линеаризованных уравнений. Рассмотрим их последовательно.
Первый, аналитический способ линеаризации, называемый также методом малых отклонений, состоит в следующем:
1) определяется рабочая точка установившегося режима работы звена (х₀,у₀), в которой необходимо определить его поведение при малых отклонениях от установившегося режима (рис. 4.7);

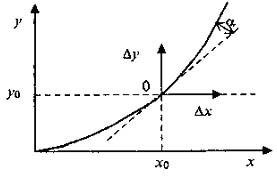
Рис. 4.7 - Линеаризация слабой нелинейности

2) нелинейная зависимость у = F(x) разлагается в ряд Тейлора в окрестности точки (х₀,у₀), в этом разложении отбрасываются члены выше первого порядка малости и получается следующая приближенная зависимость
3) полученное приближенное уравнение переписывается в виде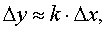
(4.9)
где
Часто в уравнениях вида (4.9) знак ∆ опускают и рассматривают линеаризованное уравнение в малых отклонениях, или, как еще говорят, в вариациях:
y = k•x. (4.10)

Рассмотрим в изложенной последовательности более общий случай, когда звено (система) описывается нелинейным уравнением вида
(4.11)
Разлагая, как и прежде, нелинейную функцию в ряд Тейлора в
точке установившегося режима, получим
(4.12)
или

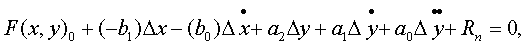
где R_n - остаточный член, определяющий члены порядка малости п≥2.
Из уравнения (4.12) вычтем уравнение (4.11) для установившегося режима работы САУ, т.е. вычтем F(x₀,0,y₀,0,0,...) = 0, и, опуская знак ∆ и отбрасывая R_n, получим линеаризованное дифференциальное уравнение динамики звена в малых отклонениях в виде (2.36) или операторной форме (2.37).
Допустимость такой линеаризации ограничена следующими условиями:
- она применима только к непрерывным дифференцируемым нелинейностям;
- она применима только для малых отклонений, т.е. полученные линеаризованные уравнения пригодны для приближенного исследования таких режимов работы системы, при которых переменные величины на ее входе имеют достаточно малые отклонения от установившихся значений, при этом точность исследования растет с уменьшением величины отклонений.
По второму, графическому способу линеаризация осуществляется на основе уравнений (4.10), (2.36) без проведения предварительных выкладок, с использованием графического смысла линеаризации. Суть состоит в замене кривой искомого решения нелинейных уравнений (4.1), (4.11) прямой, касательной к искомой кривой в точке (x₀, у₀), соответствующей начальным условиям. Угол, составленный этой касательной и осью абсцисс, будет равен (рис. 4.7). Очевидно, что такая замена справедлива только для тех отклонений ∆х, при которых кривая незначительно отклоняется от касательной. Допустимая область отклонений и определяет возможности линеаризации нелинейной системы, при этом вместо частных производных находят частные разности.
Для уравнений (4.10) и (2.36), записанных в отклонениях, графически это означает перенос начала координат в точку 0(x₀,y₀). Для реальных систем результат подобной линеаризации часто справедлив для достаточно больших значений отклонений; чем больше значения этих отклонений, тем больше к данным системам применим термин "линейная система" и тем больше степень достоверности результатов исследования САУ, полученных с помощью теории линейных систем.
Третий способ объединяет рассмотренные выше способы и предлагает сразу записывать уравнения линеаризуемого звена (системы) в отклонениях.
Четвертый способ линеаризации основан на использовании метода наименьших квадратов для определения коэффициентов уравнений (4.10) и (2.36).

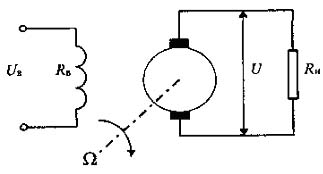
Рис 4.8 - Схема генератора постоянного тока

Рассмотрим в качестве примера вывод линеаризованного уравнения генератора постоянного тока (рис. 4.8). Такой генератор может входить в состав САУ, приведенной на рис. 2.3, в качестве электромашинного усилителя мощности.
Входной величиной генератора является напряжение возбуждения U_B, а выходной - напряжение на его выходных зажимах U. Скорость вращения якоря Ω и величину сопротивления нагрузки R_H будем считать постоянными. Реакция якоря предполагается скомпенсированной и не учитывается.
Напряжение генератора равно

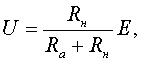
где Е - э.д.с. генератора; R_a - сопротивление цепи якоря генератора; R_H - сопротивление нагрузки.
Э.д.с. генератора пропорциональна скорости вращения якоря и магнитному потоку, т.е.

где Ω - угловая скорость вращения якоря; Ф - взаимодействующая с якорем часть магнитного потока, создаваемого обмоткой возбуждения; С₁ - коэффициент, постоянный для данной машины.
Поток Ф является функцией тока возбуждения, т.е.
Ф = F(I_B). (4.13)
Эта зависимость нелинейна (рис. 4.9).

Рис. 4.9 - Нелинейная функция тока генератора

В свою очередь, напряжение возбуждения U_в зависит от тока возбуждения: U_в = , где I_в - ток возбуждения; Rв- сопротивление цепи возбуждения; σ - число витков обмотки возбуждения; - коэффициент рассеяния магнитного потока, с помощью которого полный поток, создаваемый обмоткой возбуждения, выражается в виде σФ ( σ > 1). Таким образом, полученные четыре уравнения в совокупности определяют искомую зависимость U от U_в через промежуточные переменные Е, Ф и I_в. Эта зависимость нелинейна из-за нелинейности характеристики намагничивания генератора (4.13) и обусловлена насыщением магнитной цепи, а также гистерезисом. Петля гистерезиса (рис. 4.9) узка, ею можно пренебречь и ограничиться основной кривой намагничивания, показанной на рис. 4.9 сплошной линией. Переходя в уравнениях к приращениям переменных, получим следующую систему линейных уравнений:

где (dФ/dI_в)₀ определяется как тангенс угла наклона касательной к основной кривой намагничивания в точке установившегося режима (рис. 4.9).
Исключив из системы (4.14) промежуточные переменные ∆Е, ∆Ф и ∆I_в получим искомое линеаризованное уравнение, связывающее ∆U с ∆U_в:
(Tвp+1) ∆U=k_в1∆U_в, (4.15)
где Тв - постоянная времени цепи возбуждения:

k_в1 - коэффициент передачи генератора по возбуждению:

Заметим, что Тв и k_в1 зависят от выбранной точки установившегося режима, в которой осуществляется линеаризация.
Если перейти к относительным единицам, то линеаризованное уравнение (4.15) примет следующий вид:
(Tвp +1)u = k_в2U_в, (4.16)
где u=∆U/U_в; U_в=∆U_в/U_в0; k_в2=k_в1U_в0/U_в.
С использованием оператора передаточной функции получим следующее выражение:
u=Wв(p)U_в, (4.17)
где

В заключение отметим, что при выводе уравнений (4.16), (4.17) скорость вращения якоря и сопротивление нагрузки были приняты постоянными. Если учесть их непостоянство, то в правой части этих уравнений появятся дополнительно второй и третий члены.
Изложенные выше способы линеаризации относительно рабочей точки установившегося режима или положения равновесия нелинейной системы можно без труда обобщить, проводя линеаризацию относительно некоторого решения или траектории движения системы. Этот прием успешно применяется, например, в задачах космической навигации, когда известна расчетная траектория движения объекта (космического корабля). После линеаризации исходных уравнений оказывается возможным определить управляющие воздействия, которые будут удерживать космический корабль вблизи расчетной траектории.
Анализируя полученные линеаризованные уравнения, можно оценить влияние ошибок при задании начальных условий и параметров объекта, определить функции чувствительности.
Полученные при линеаризации линейные уравнения, как правило, нестационарны, а имеющиеся теоретические результаты исследования линейных систем (см. раздел 3) относятся в основном к стационарным линейным системам.
Для нестационарных систем теория, с одной стороны, находится в стадии разработки, а с другой - сложна в приложениях. И самое главное, в случае нестационарной системы следует постоянно помнить о степени малости и задавать себе вопрос, достаточно ли малы изменения переменных и остаются ли они в области, где линеаризованные уравнения справедливы.
Если имеются сомнения, то решения линеаризованного уравнения должны постоянно сравниваться с численным решением исходного нелинейного уравнения.
Если линеаризованные уравнения адекватны решаемой нелинейной задаче, то их полное решение может быть легко выписано, а изложенные в разделах 2 и 3 методики удобны для их исследования.
Ситуация совсем иная, если дифференциальные уравнения звеньев, а значит и системы в целом, не линеаризуются переходом к малым колебаниям около положения исследуемого равновесия. Не только общее решение, но даже поиск периодических решений является сложной и не всегда преодолеваемой до искомого решения задачей. Теория нелинейных САУ создавалась путем постепенного преодоления этих трудностей.

4.3 Устойчивость нелинейных систем

Понятие устойчивости естественно и просто введено в подразделе 3.2 для линейных систем. Там же сформулированы необходимые и достаточные условия устойчивости. Для стационарных линейных систем единственным положением равновесия будет начало координат, если выполнено два условия: характеристическое уравнение системы не имеет полюсов с действительной частью, а входной сигнал равен нулю. На этой основе определены два эквивалентных условия устойчивости (или неустойчивости) положения равновесия (начала координат) системы.
1. Система устойчива (или неустойчива) при отсутствии входного сигнала, если при произвольных начальных условиях фазовые траектории стремятся к началу координат (или уходят в бесконечность).
2. Система устойчива (или неустойчива) при ограниченном входном сигнале, если выходной сигнал ограничен (или неограничен).
Первое условие определяет поведение свободной системы в переходном процессе, а второе - поведение системы при неравном нулю входном сигнале. Оба условия устойчивости эквивалентны для стационарных линейных систем.
В нелинейных системах нет такой простой связи между этими двумя типами устойчивости, так как свободное движение системы может существенно отличаться от вынужденного.
Рассмотрим в качестве примера нелинейную систему первого порядка, описываемую уравнением вида 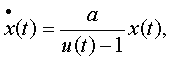где а > 0.При u(t) ≡ О система устойчива, но при u(t) ≠ О всякий раз, когда управление u(t)=1, x(t)→∞ ; если u(t) = const > 1, то реакция системы также не ограничена. Следовательно, нельзя гарантировать ограниченность реакции при ограниченном управлении, т.е. в рамках второго определения вопрос об устойчивости нелинейной системы не решается.
В этой связи анализ устойчивости нелинейных систем проводится в рамках первого определения. Однако для нелинейных систем вопрос об устойчивости значительно сложнее. При исследовании нелинейных систем используются понятия устойчивости в малом, в большом, в целом, абсолютная устойчивость:

- устойчивость в малом - это устойчивость при бесконечно малых отклонениях относительно исходного режима (положения равновесия);
- устойчивость в большом - это устойчивость при конечных отклонениях относительно положения равновесия, возможных в данной системе по условиям ее работы;
- устойчивость в целом - это устойчивость при любых отклонениях от исходного режима, т.е. при отсутствии каких-либо ограничений (при любых начальных условиях);
- абсолютная устойчивость - это асимптотическая устойчивость системы в целом при любом характере нелинейности внутри определенного класса нелинейностей.
Поясним на примере трудности анализа нелинейных систем. Пусть поведение системы описывается уравнением Ван-дер-Поля:

Решение этого уравнения для μ=0,2 представим в виде
фазовых траекторий на фазовой плоскости 0х₁x₂ (рис. 4.10).

Рис. 4.10 - Фазовый портрет для системы (4.18)

Поясним использованные термины.
Фазовое пространство. Текущие значения координат x₁,x₂,...,x_n нелинейной системы удобно представлять в виде точки в n-мерном декартовом пространстве, называемом пространством состояний или фазовым пространством системы. Дифференциальные уравнения системы, записанные в нормальной форме (2.42), определяют значения проекций вектора скорости, с которой будет перемещаться данная точка фазового пространства.
фазовые траектории. Точка фазового пространства, соответствующая состоянию системы в данный момент времени, называется изображающей точкой. Геометрическое место изображающих точек, соответствующее последовательному изменению состояния системы со временем в фазовом пространстве, называется фазовой траекторией или интегральной кривой. Полная совокупность интегральных кривых, соответствующая всем возможным начальным условиям, называется фазовым портретом системы.
Фазовая плоскость. Фазовая плоскость является частным случаем фазового пространства и используется для исследования нелинейных систем, описываемых уравнениями первого и второго порядков. Если

Это уравнение фазовой траектории - интегральной кривой на фазовой плоскости.
Вблизи начала координат (рис. 4.10) фазовые траектории 1 раскручиваются и стремятся к замкнутой траектории (предельному циклу). Фазовые траектории 2, начинающиеся вне предельного цикла, также со временем сходятся к нему. Следовательно, система, описываемая уравнением (4.18), неустойчива в "малом" относительно положения равновесия, но при этом всякое движение со временем переходит в предельный цикл. Если амплитуда предельного цикла оказывается малой, то такое поведение системы при больших сигналах оказывается приемлемым, т.е. система, неустойчивая при малых отклонениях от положения равновесия, практически устойчива при значительных отклонениях.
Подведем предварительные итоги изложенных выше рассуждений:
- в отличие от линейных систем для нелинейных систем следует говорить об устойчивости относительно положения равновесия, а не об устойчивости системы вообще;
- устойчивость в малом еще не определяет устойчивость во всем фазовом пространстве (пространстве состояний системы), и эти две задачи следует изучать раздельно;
- даже при анализе устойчивости в малом следует рассматривать два случая: либо все фазовые траектории системы никогда не покидают некоторой определенной окрестности положения равновесия, либо все траектории асимптотически приближаются к рассматриваемому положению равновесия.
Впервые свойства устойчивости в изложенном выше понимании были исследованы русским ученым A.M. Ляпуновым в 1892 г. в работе "Общая задача об устойчивости движения".

4.3.1 Устойчивость в малом (устойчивость по Ляпунову)

 

Запишем уравнения динамики системы n-го порядка в общем нелинейном виде в нормальной форме Коши:
dx_n/dt = F_k(x₁,x₂,...,x_n,t), k = 1,2,...,n, (4.19)
где x₁,x₂,...,x_n - величины, определяющие состояние системы в каждый данный момент времени;
F_k - некоторые нелинейные функции.
Заметим, что в частном случае линейной системы уравнения (4.19) перепишутся в форме (2.42).
Наличие t под знаком функции F_k(k = 1,2,...,п) объясняется либо тем, что на систему действуют изменяющиеся во времени внешние воздействия, либо тем, что некоторые параметры системы изменяются во времени. Системы, описываемые уравнениями вида (4.19), с правыми частями, зависящими только от величин x₁,x₂,...,x_n и не зависящими явно от времени t, называются автономными.
Будем считать, что функции F_k(k=1,2,...,n) таковы, что при заданной совокупности начальных условий x_k(t₀) = x_k0 (k=1,2,...,n), t=t₀ - произвольный момент времени, принимаемый за начальный, существует единственное решение системы уравнений (4.19). Из совокупности возможных решений системы уравнений (4.19) выберем одно x_k=x*_k(t) (k=1,2,...,n), отвечающее определенным начальным условиям, которое назовем невозмущенным движением системы. Всякое другое движение, отличное от невозмущенного (соответствующее другим начальным условиям), будем называть возмущенным.
Выбор невозмущенного движения произволен. Обычно невозмущенным движением называют такое, которое инженер принимает за расчетное движение системы. От этого движения систему отклоняют различные возмущения. Сформулируем определение устойчивости по A.M. Ляпунову.
Невозмущенное движение называется устойчивым по Ляпунову, если для всякого ε > 0 можно указать δ > 0 такое, что из неравенства

следует при всех t≥t₀ неравенство
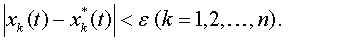(4.21)
Невозмущенное движение x*_k(t) называется асимптотически устойчивым по Ляпунову, если оно устойчиво в смысле Ляпунова и если существует такое положительное h, что при будем иметь
(4.22)
Если существует хотя бы одно такое число ε > 0, что при любом сколь угодно малом δ > 0 существует возмущенное движение, удовлетворяющее условию (4.20), для которого при некоторых значениях t>t₀неравенства (4.21) не выполняются, то невозмущенное движение называется неустойчивым.
Этим определениям можно дать геометрическую интерпретацию. Будем изображать отклонение возмущенного движения системы от невозмущенного в каждый момент времени t точкой n-мерного пространства с прямоугольными декартовыми координатами

На рис. 4.11 представлена геометрическая интерпретация определений устойчивости по A.M. Ляпунову. Заметим, что в приведенных выше аналитических определениях области ε и δ, в отличие от рис. 4.11, выглядят гиперкубическими (в n-мерном пространстве), но это не имеет принципиального значения.
Невозмущенное движение (в данном случае начало координат) устойчиво (рис. 4.11. а), если при любом как угодно малом радиусе ε сферы С_ε существует такая сфера С_δ радиусом δ, что изображающая точка не может выйти за пределы сферы С_ε, начав движение из любой точки сферы С_δ.

Невозмущенное движение асимптотически устойчива (рис. 4.11, б), если существует такая сфера С_δ, что изображаю, щая точка стремится к началу координат, начав движение из лю-бой точки сферы С_δ.

Рис. 4.11 - Устойчивость по Ляпонову

Невозмущенное движение неустойчиво (рис. 4.11, в), если существует такая сфера С_ε и как угодно близко к началу коор-динат можно найти такую точку М_o, что изображающая точка М выйдет за пределы сферы С_ε, начав движение из точки М_o.
В определении устойчивости по Ляпунову невозмущенное и возмущенное движения рассматриваются всегда при одних и тех же входных сигналах системы, представляющих собой вполне определенные функции времени. Поэтому одна и та же система при одних и тех же начальных условиях невозмущенного движения t_o,x*₁₀,...,x*_n0 может быть устойчивой по Ляпунову при одних входных сигналах и неустойчивой при других входных сигналах.
Межде тем в задачах практики приходится оценивать устойчивость работы системы при различных заранее неизвестных входных сигналах, что делает определение устойчивости по Ляпунову недостаточным для практики.
Приведем еще одно определение устойчивости, учитывающее изменение как начальных условий, так и входного сигнала, т.е. оба условия устойчивости, эквивалентных для линей-ных систем и сформулированных в самом начале настоящего подраздела.
Будем считать, что при изменении формы входных сигналов правые части дифференциальных уравнений (4.1) изменяются непрерывно, т.е. при замене входных сигналов достаточно близ-кими к ним другими входными сигналами функции F_k в уравнениях (4.19) изменяются сколь угодно мало. В этом случае дифференциальные уравнения возмущенных движений можно написать в виде
x_k=F_k(x₁,...x₁,t) + φ_k(x₁,...x_n,t)t (k = l,2,...,n), (4.23) где φ_k - функции, сколь угодно малые по абсолютной величине при любых достаточно малых отклонениях входных сигналов системы от входных сигналов, соответствующих невозмущенному движению.
Различным входным сигналам системы соответствуют различные функции φ_k в уравнениях (4.23). В частности, φ_k =0 для невозмущенного движения.
Назовем невозмущенное движение системы устойчивым, если отклонение ее возмущенного движения от невозмущенного остается сколь угодно малым при любых достаточно малых начальных отклонениях и при любых входных сигналах, достаточно близких к входным сигналам, соответствующим невозмущенному движению. В аналитической форме это определение понятия устойчивости формулируется следующим образом.
Невозмущенное движение системы называется устойчивым, если при сколь угодно малом ε > 0 существуют такие числа δ = δ(ε) и δ' = δ'(ε) , что для всех возмущенных движений, Удовлетворяющих условию (4.20), при любом t > t₀ выполняются неравенства (4.21), если |φk,(x*₁,...,x*_n,t)|<δ' (к = 1,2,...,n).
Доказано, что при довольно общих условиях невозмущенное движение системы устойчиво в смысле данного определения, если оно асимптотически устойчиво по Ляпунову, т.е. исследование устойчивости нелинейной системы практически сводится к исследованию ее асимптотической устойчивости. Имен-но этим объясняется большое практическое значение теории устойчивости движения, созданной A.M. Ляпуновым.

4.3.2 Первый метод Ляпунова

Первый метод Ляпунова основан на линеаризации уравнений, описывающих поведение системы.
Линеаризация осуществляется разложением всех входящих в уравнение (4.19) функций F_k(k = 1,2,...,л) в ряд Тейлора и отбрасыванием всех членов выше первой степени относительно величин η₁ = x₁ - х*₁; η₂ = х₂ - х*₂,...; η_n = x_n - х*_n , т.е.
F_k(x₁,...,x_n,t) ≈ F_k(x*₁,...,x*_nt) + (4.24)

Подставляя (4.24) в (4.19) и учитывая, что невозмущенное движение удовлетворяет (4.19), т.е. x*_k=F_k(x*₁,...,x*_n,t), (к=1,...,n), получим систему линейных дифференциальных уравнений относительно η₁,η₂,...,η_n
(4.25)

величины η₁,η₂,...,η_n определяют отклонение возмущенного движения от невозмущенного. Их принято называть вариациями переменных x₁,x₂,...,x_n, определяющих состояние системы. Приближенные линейные уравнения (4.25) называются уравнениями в вариациях или линейными уравнениями первого приближения.
Приведем без доказательства теоремы A.M. Ляпунова, справедливые для автономных систем, для которых a_ki(t) = a_ki - const, а характеристическое уравнение первого приближения определяется выражением (2.43).
Теорема 4.1. Если вещественные части всех корней характеристического уравнения первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво независимо от членов разложения выше первого порядка малости.
Теорема 4.2. Если среди корней характеристического уравнения первого приближения найдется по меньшей мере один с
положительной вещественной частью, то невозмущенное движение неустойчиво независимо от членов разложения выше первого порядка малости.
Данные теоремы позволяют однозначно разрешить вопрос об устойчивости (или неустойчивости) невозмущенного движения автономной нелинейной системы на основании исследования уравнений первого приближения только для структуры корней характеристического уравнения, указанной в условиях теорем. Если структура корней характеристического уравнения другая, то для определения характера устойчивости одних уравнений первого приближения недостаточно и необходимо рассмотреть влияние членов второго и высшего порядка малости, т.е. нужно оценивать устойчивость движения исходной системы уже по исходным уравнениям (4.19).
В общем случае, когда коэффициенты a_ki(t) уравнений
(4.25) являются любыми функциями времени, для исследования устойчивости движения можно применить общее необходимое и достаточное условие устойчивости линейной системы (3.38). Для этого необходимо определить весовые (импульсные переходные) функции ω_ij(t,τ) линеаризованной системы, описываемой уравнениями в вариациях (4.25), соответствующие всем входам (j=1,...,m) системы и всем переменным x_i(i = 1,...,n), и вычислить для них интегралы вида
(i=1,...,n; j=1,...,m) (4.26)

Выполнив эти вычисления для различных моментов времени t, можно судить об устойчивости системы. Если интегралы (4.26) для весовых (импульсных переходных) функций, соответствующих всем входам системы и всем переменным x₁,...,х_n;, перестают заметно изменяться с увеличением t , начиная с некоторого момента, то исследуемое невозмущенное движение нелинейной системы устойчиво по отношению к переменным x₁,...,х_n. Если же хотя бы один из интегралов (4.26) неограниченно возрастает с увеличением t , то невозмущенное движение нелинейной системы неустойчиво. Изложенный способ исследования устойчивости основан на пракгике анализа и моделирования реальных систем и не позволяет делать строгие выводы об Устойчивости или неустойчивости из-за невозможности осуществить путем расчетов на ЭВМ бесконечные процессы, связанные с предельным переходом в формуле (3.38).

Однако на практике такой способ исследования устойчи вости позволяет безошибочно судить об устойчивости невозмущенного (расчетного) движения нелинейной системы в течение любых интересующих исследователя интервалов времени.
В заключение еще раз подчеркнем, что изложенный метод исследования устойчивости нелинейных систем, основанный на линеаризации уравнений, описывающих поведение системы, применим лишь к системам, содержащим только элементарные нелинейные звенья с непрерывными гладкими характеристиками. К системам с существенными нелинейностями этот метод не применим. В таких случаях оказывается полезным следующий, второй метод Ляпунова.

4.3.3 Второй (прямой) метод Ляпунова

Второй метод Ляпунова связан с физическими представлениями о равновесии материальной точки в консервативном силовом поле. Из физики известно, что точки минимума потенциальной энергии являются положениями устойчивого равновесия материальной точки (рис. 3.6, а), а точки максимума потенци альной энергии - положениями неустойчивого равновесия (рис. 3.6, б). Основная идея второго метода Ляпунова состоит в нахождении такой функции координат точки пространства со стояний системы V(η₁,...,η_n) , которая была бы до некоторой степени аналогична потенциальной энергии покоящейся материальной точки в обычном пространстве.

Введем некоторые определения.

Функция V(η₁,...,η_n) называется знакопостоянной, если она имеет один и тот же знак всюду в некоторой области, содержащей начало координат, за исключением некоторых точек, в которых она равна нулю.

Знакопостоянная функция, равная нулю лишь в начале координат, называется знакоопределенной : определенно - положительной или определенно - отрицательной, в зависимости от знака. Например, в трехмерном пространстве (n = 3) функция

V = а²η₁² + b²η₂² + c²η₃² является знакоопределенной функцией, а функция V = (η₁ + η₂)² + c²η₃² - знакопостоянной функцией, которая обращается в нуль на прямой η₂ = -η₁ и η₃ = 0
A.M. Ляпунов доказал следующие две теоремы.
Теорема 4.3. Если дифференциальные уравнения возмущенного движения таковы, что можно найти знакоопределенную функцию V, полная производная которой по времени

(4.27)
в силу этих уравнении знакопостоянна и имеет знак, противоположный знаку функции V , или тождественно равна нулю, то невозмущенное движение устойчиво.
Доказательство теоремы. Выбираем произвольное достаточно малое ε > 0 и построим сферу

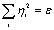(Рис. 4.12)

Рис. 4.12 - Устойчивость по Ляпунову

Затем построим поверхность V = С, лежащую внутри сферы ε. Это можно всегда сделать, так как функция V непрерывна и равна нулю в начале координат. Выбеоем теперь число δ настолько малым, чтобы сфера целиком лежала внутри поверхности V = С, не имея с ней общих точек. Покажем, что изображающая точка М, начав движение из сферы δ никогда не дойдет до сферы ε, что и будет служить доказательством Устойчивости движения.
Не нарушая общности, можно считать, что функция V определенно-положительная (если V<0, то можно взять функцию минус V).

По условию теоремы ее производная, вычисленная в силу уравнений возмущенного движения, будет отрицательной или тождественно равной нулю функцией V≤0, т.е. функция V(η(t)) - невозрастающая функция. Тогда из соотношения 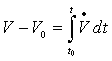, где V₀ - значение V в точке М₀, будем иметь V - V₀≤ 0, или V ≤ V₀. Отсюда следует, что при t≥t₀ изображающая точка М либо находится на поверхности V = V₀ = C₁ (при 0), либо внутри этой поверхности. Таким образом, изображающая точка М, начав движение из точки М₀ принадлежащей сфере δ, никогда не выйдет за пределы поверхности V = С₁, и тем более не сможет достичь сферы ε.
Приведем пример, иллюстрирующий теорему 4.3.
Пусть уравнения возмущенного движения имеют вид:

Возьмем определенно-положительную функцию

и вычислим ее производную по времени. В силу уравнений возмущенного движения имеем . Подставляя вместо и их значения из уравнений возмущенного движения, получим

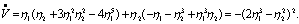
Так как функция V определенно-положительная, а ее производная отрицательная функция, то выполнены условия теоремы Ляпунова об устойчивости движения и, следовательно, невозмущенное движение η₁=0, ┧₂=0 устойчиво.
Теорема 4.4. Если дифференциальные уравнения возмущенного движения таковы, что можно найти знакоопределенную функцию V, полная производная которой по времени в силу этих уравнений знакоопределенна и имеет знак, противоположный знаку функции V, то невозмущенное движение асимптотически устойчиво.
Геометрическая иллюстрация теоремы Ляпунова об асимптотической устойчивости может быть представлена тем же рис.4.12, но с той разницей, что при V > 0 имеем < 0. При этом по свойству (4.27) фазовая траектория, пересекая поверхности V=const извне внутрь, не может оставаться на них, а пойдет внутрь до начала координат, η_i=0 (i=1,...,n) и V=0 . Ход аналитического доказательства теоремы 4.4 остается тем же, что и теоремы 4.3, но с изменением неравенств "≤" на " < ".
Функции V, удовлетворяющие условиям теорем 4.3, 4.4, называются функциями Ляпунова.
Второй (прямой) метод оценки устойчивости по Ляпунову дает достаточные условия устойчивости, т.е. движение системы может быть устойчивым и при невыполнении условий теорем 4.3, 4.4 Ляпунова.
Метод исследования устойчивости с помощью функции Ляпунова V(η₁,...,η_n) эффективен и применим к любым нелинейным системам, так как он не накладывает каких-либо ограничений на правые части уравнений движения системы. Однако практическое применение этого метода осложнено трудностью нахождения функции Ляпунова V(η₁,...,η_n). Общих рекомендаций по нахождению этой функции для произвольных систем не существует. A.M. Ляпунов указал один метод нахождения функции V для линейных систем.
Для иллюстрации идеи второго (прямого) метода Ляпунова рассмотрим простой пример. Пусть имеется система уравнений

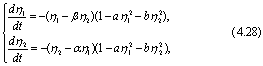
где - положительные постоянные коэффициенты.
Предложим для этой системы следующую функцию:

(4.29)
Ее производная равна
Подставив сюда выражение (4.28), получим

Производная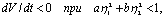
т.е. внутри эллипса движение устойчиво и фазовые траектории скручиваются к началу координат. Движение вне этого эллипса неустойчиво. Сам эллипс представляет собой неустойчивый предельный цикл.
Этот пример иллюстрирует редкий (счастливый) случай, когда не только находится функция Ляпунова, но и полностью определяется область, внутри которой состояние равновесия остается устойчивым.

4.3.4 Проблема Айзермана. Критерий абсолютной устойчивости В.М. Попова

Абсолютная устойчивость - это устойчивость в целом нелинейной системы при задании ее нелинейностей принадлежностью к определенному классу. Под этим понимается задание нелинейности не конкретной характеристикой, а в более общем виде с точностью до определения класса нелинейностей.
Наиболее разработаны методы исследования абсолютной устойчивости для нелинейных систем (рис. 4.13), состоящих из линейного звена и нелинейной обратной связи, статическая характеристика которого представлена на рис. 4.14, т.е. статическая нелинейная характеристика находится в определенном угле между прямыми линиями λ₁x и λ₂x.

Рис. 4.13 - Нелинейная система (пример)

 

Рис. 4.14 - К понятию абсолютной устойчивости

Это условие обычно записывается в виде
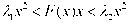(4.30)
для всех х ≠ 0.
Если в системе такого типа положить F = λx, то в плоскости х, F(x) может быть проведен луч через начало координат, такой, что при любом х из этого луча соответствующая линейная система устойчива.
В 1949 г. М.А. Айзерман выдвинул гипотезу о том, что если асимптотически устойчивы все линейные системы, для которых
(φ) = λ(λ = const) и выполнено условие (4.30), то этим же свойством обладает все семейство нелинейных систем, характеризующееся условием (4.30). Такие системы были названы абсолютно устойчивыми. Исследования показали, что для систем второго порядка гипотеза верна, исключая случай асимптотического приближения траектории к краям луча, но для систем более высокого порядка были разработаны примеры, противоречащие этой гипотезе. В 1951 г. А.И. Лурье предложил использовать функцию Ляпунова, квадратичная форма которой дополнена интегралом от нелинейной характеристики F(x) или F(x,t). Однако это дополнение лишь расширило луч, обеспечивающий абсолютную устойчивость. В 1960 г. на первом конгрессе ИФАК румынский ученый В.М. Попов доложил неожиданный результат : можно построить аналог частотной характеристики линейной части системы, которого достаточно для определения луча. Рассмотрим подробнее критерий абсолютной устойчивости В.М. Попова.
Характеристика F(x) (рис.4.13) однозначна и лежит в углу
(0,k), т.е. (λ₁ = 0, λ₂ = k). Для определения устойчивости по этому критерию используется частотная характеристика

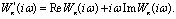
Эта характеристика получается из АФХ W_л(iω) линейной части системы путем умножения ординат последней характеристики на текущее значение ω.
Рассмотрим вначале критерий В.М. Попова для случая, когда линейная часть системы устойчива. Система абсолютно устойчива, если при устойчивой линейной части системы через точку (-1/k,i0) можно провести хотя бы одну прямую линию так, чтобы характеристика W*_л(iω) находилась от нее справа (рис. 4,15). Такая линия называется линией Попова

Рис. 4.15 - Критерий В.М.Попова для системы с устойчивой линейной

частью: а - критерий выполняется, б - критерий не выполняется

Критерий В.М. Попова является достаточным, т.е. он дает часть области абсолютной устойчивости и его невыполнение не означает отсутствия абсолютной устойчивости.
Чтобы распространить этот критерий на системы с неустойчивой линейной частью, преобразуем предварительную схему системы (см. рис. 4.13): введем два фиктивных звена с коэффициентом передачи к_ф (рис. 4.16). Они ничего не изменят в системе, так как их выходные сигналы взаимно компенсируют друг друга на входе линейной части системы.
В результате получим систему, состоящую из линейной части передаточной функиции

и нелинейной части с характеристикой F_ф(x) = F(x) - k_фx
Выберем величину k_ф такой, чтобы новая линейная часть оказалась устойчивой. Применим к преобразованной системе с устойчивой линейной частью критерий В.М. Попова.

В результате получим следующее условие абсолютной устойчивости исходной системы с неустойчивой линейной частью : система абсолютно устойчива, если через точку (-1/(к-k_ф),0) можно провести прямую линию, проходящую слева от характеристики W*_лф(iω), т.е. характеристика F(x) (рис.4.16, б) должна лежать в углу (k_ф,к).

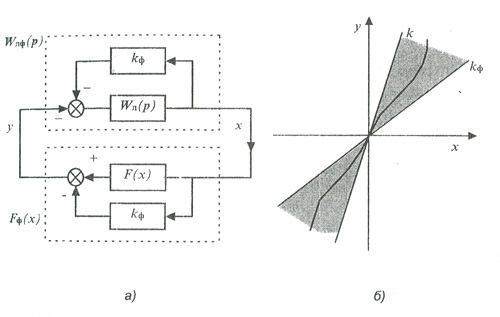
Рис. 4.16 - К абсолютной устойчивости системы с неустойчивой линейной частью

 

Этот вывод следует из того, что характеристика F_ф(х) (4.31) расположена в угле [0, (к-к_ф)\.
В 1966 г. В.М. Попов доказал, что аналогично может быть определен луч, который обеспечивается как функцией Ляпунова в виде квадратичной формы, так и функцией Ляпунова в форме Лурье.
Исследования по проблеме абсолютной устойчивости продолжаются, но найти наиболее широкий луч абсолютной устойчивости до сих пор не удалось.

4.4 Исследование нелинейных систем методом точечных преобразований

Метод точечных преобразований (отображений), берущий свое начало от Пуанкаре и Биркгофа, был впервые введен в ТАУ А.А. Андроновым. Основные общие рекомендации по применению теории точечных отображений к изучению конкретных нелинейных САР и радиотехники сформулированы А.А. Андроновым в 1944 г. в докладе на сессии отделения физико-математических наук АН СССР "Теория точечных преобразований Пуанкаре-Брауера-Биркгофа и теория нелинейных колебаний". В это же время им был решен ряд основных нелинейных задач ТАР, в том числе и классическая задача И.А. Вышнеградского о регуляторе прямого действия с сухим трением в чувствительном элементе. В основе этих и многочисленных последующих работ (продолжающихся и в настоящее время) лежит кусочно-линейная аппроксимация нелинейностей, которая обеспечивает получение аналитических выражений точечного преобразования в явном или параметрическом виде. Именно этим обстоятельством объясняется то, что в учебной и справочной литературе по ТАУ метод точечных отображений определен как метод исследования кусочно-линейных систем невысокого порядка. Ю.И. Неймарк в монографии "Метод точечных отображений в теории нелинейных колебаний" (1972 г.) отмечает, что сам А.А. Андронов рассматривал кусочно-линейные системы как частный тип нелинейных систем, для которых исследование методом точечных преобразований может обеспечить быстрый успех, а исследование кусочно-линейных систем, как старт развитию метода точечных преобразований применительно к задачам теории колебаний. Ю.И. Неймарк и его нижегородская научная школа рассматривают точечные отображения в качестве общего средства описания и эффективного аппарата исследования теории колебаний как науки об общих закономерностях динамических процессов.
Для пояснения идеи метода точечных преобразований предположим, что изображающая точка в какой-то момент времени занимает положение X (рис. 4.17) с координатой х на положительной полуоси 0x₁. После обхода вокруг начала координат изображающая точка пересечет полуось 0x₁ в некоторой точке Y, имеющей координату у. Через каждую точку полуоси 0x₁ можно провести одну и только одну фазовую траекторию, поэтому обходу изображающей точки вокруг начала координат соответствует переход каждой точки полуоси 0x₁ в некоторую другую точку той же полуоси.

Рис. 4.17 - Точечное преобразование полуоси Ох₁ в саму себя

Другими словами, обходу изображающей точки вокруг начала координат (либо другой особой точки на фазовой плоскости) соответствует точечное преобразование любой полуоси (в общем случае - полупрямой), выходящей из начала координат, в саму себя. Если при этом преобразовании какая-нибудь точка полуоси (полупрямой) переходит в саму себя, т.е. остается неподвижной, то через эту точку проходит замкнутая фазовая траектория - предельный цикл. Таким образом, для нахождения предельных циклов и определения параметров соответствующих автоколебаний достаточно найти неподвижные точки точечного преобразования какой-либо полупрямой, выходящей из соответствующей особой точки фазовой плоскости.
Каждой точке выбранной полупрямой соответствует некоторое положительное число, равное расстоянию этой точки от начала координат (или от соответствующей особой точки).
Поэтому точечное преобразование выбранной полупрямой при обходе изображающей точки вокруг начала координат (особой точки) определяет однозначную возрастающую функцию y=f(x), которая может быть изображена кривой в координатах 0xy (рис. 4.18).
Определение у по х (т.е. нахождение точки Y по точке X) называется точечным преобразованием. Зависимость y=f(x) описывает точечное преобразование положительной полуоси 0x₁ в саму себя, происходящее при обходе изображающей точки начала координат.
Каждая точка этой кривой с одинаковыми абсциссой и ординатой, т.е. точка пересечения ее с биссектрисой (рис. 4.18 -штрих-пунктирная линия) координатного угла у=х является неподвижной точкой преобразования, определяет предельный цикл и амплитуду возможных автоколебаний в системе.

Рис 4.18 - Функция точечного преобразования

Участкам кривой у = f(х), лежащим ниже биссектрисы координатного угла у=х, соответствуют спиральные фазовые траектории, по которым изображающая точка приближается к началу координат, т.е. колебательный процесс является затухающим. Участкам кривой у = f(x), лежащим выше биссектрисы координатного угла у=х, соответствуют спиральные фазовые траектории, по которым изображающая точка удаляется от начала координат, следовательно, колебательный процесс является расходящимся. Таким образом, вид функции у = f(x) и взаимное расположение кривой точечного преобразования у=f(x) и биссектрисы координатного угла у=х позволяют судить' о характере поведения нелинейной системы около положения равновесия. При этом, если кривая y=f(x) пересекает биссектрису у=х сверху вниз (рис. 4.18 - точка 2), то автоколебания устойчивы, а если снизу вверх (рис. 4.18 - точка 1) - неустойчивы.
Метод точечных преобразований позволяет исследовать характер возможных режимов в системе, не строя фазового портрета. Метод удобен, в частности, для определения влияния изменения разных параметров системы на характер переходных процессов в ней. При этом могут быть определены критические, так называемые бифуркационные значения параметров, переход через которые качественно меняет фазовый портрет системы.
Для иллюстрации на рис. 4.19 показано возможное изменение диаграммы точечного преобразования системы при вариации ее параметров. График 3 соответствует устойчивости в целом. Кривая 2 касается биссектрисы в точке, соответствующей полуустойчивому циклу. Эта кривая определяет бифуркационные значения параметров системы, при которых система находится на границе между качественно различными типами фазового портрета.

Рис. 4.19 - Влияние параметров системы на диаграмму точечного преобразования

При бесконечно малом отклонении параметров в одну сторону система становится устойчивой в целом (рис.4.19 - кривая 3), а при отклонении параметров в другую сторону система становится устойчивой только в малом с переходом к устойчивым автоколебаниям при больших отклонениях от установившегося режима (рис. 4.19 - кривая 1). Заметим, что если кривая y=f(x) и прямая у=х не пересекаются (рис. 4.19 - кривая 3), то предельного цикла не существует и автоколебания в системе невозможны.
Для многих систем фазовая плоскость оказывается симметричной относительно оси абсцисс и оси ординат. При исследовании таких систем удобно рассматривать преобразование полуоси x₁ > 0 в полуось x₁ < 0 при полуобходе изображающей точки вокруг начала координат.
Этому полуобходу также соответствует некоторая функция y=f(х).
Если на фазовой плоскости имеются линии переключения, то удобнее изучать точечные преобразования какой-нибудь линии переключения в саму себя.
Метод исследования нелинейных систем с помощью фазовой плоскости и метод точечных преобразований наглядны и сравнительно просты для систем второго порядка. Для систем третьего порядка эти методы значительно усложняются. Для систем выше третьего порядка точные методы исследования нелинейных систем в своей традиционной форме практически неприменимы.
Существует 55-летняя традиция успешного применения метода точечных преобразований для исследования кусочно-линейных систем невысокого порядка. Решим задачу составления уравнений точечных преобразований на примере исследования следящей системы. Уравнение для отклонений данной системы при наличии сил сухого трения имеет следующий вид:
(4.32)
Легко увидеть, что уравнение (4.32) является частным случаем рассмотренной выше динамической нелинейности (4.6).
В данном примере исследуется свободное движение следящей системы (правая часть уравнения равна нулю) и предполагается
отсутствие застоев (4.7), т.е. характеристика сухого трения сводится к идеальной релейной характеристике (см. рис. 4.3, а, рис. 1.8, б-1), поэтому отсутствует второй член из уравнения (4.6). Следовательно, (4.6) для нашего примера запишется в виде
mp²y + csignpy + k₂y = 0. (4.33)
Разделив каждое слагаемое на массу m и произведя замену у=х; А=с/m; , получим из (4.33) уравнение (4.32). При уравнение (4.32) линейно и его решение
, (4.34)
где В определяется из начальных условий.
В нашем примере уравнение линии переключения . Построим точечное преобразование этой линии переключения в саму себя. Пусть , тогда согласно (4.34) имеем x(t_1i) = B_icosω₀t₁ + A, а при из (4.34) получим x(t_2j) = -C_jcosω₀t₂ - A, где B_i и С_j - постоянные, зависящие от начальных условий и числа переключений на линии . Определим разностное уравнение, связывающее между собой
значения В и С.
Пусть условие выполняется с момента времени t_1,2k, тогда спустя полпериода имеем
-B_2k+A = -C_2k+1 - A. (4.35)
Спустя еще полпериода будем иметь
C_2k+1 - A = B_2k+1 + A. (4.36)
Уравнения (4.35) и (4.36) являются уравнениями точечных преобразований и позволяют вычислить значение C_2k+1, если известно B_2k, а если известно C_2k+1, то вычислить значение B_2(k+1). Из уравнений (4.35) и (4.36) получим, например, следующее соотношение: В_i+1 = В_i - 4А, где i = 2k . Задавая В₀ = х-А, получим B₁ = x - 5A, В₂ = x - 9А и т.д.
Решение заканчивается, когда В_i, становится меньше А.
Продолжим изучение этого примера и построим фазовый портрет следящей системы при учете сил сухого трения. При А=0 система консервативна и решение (4.34) запишется в виде x=Bcosω₀t. Обозначая х = х₁, , получим:
;

или
Интегрируя это выражение и считая знак х₂ неизменным, получим

где d определяется начальными условиями. Введя относительную координату , получим

Это уравнение окружности, координаты центра которой смещены относительно начала координат по оси ω на величину минус
На рис. 4.20 представлено семейство фазовых траекторий, соответствующее рассматриваемому случаю.

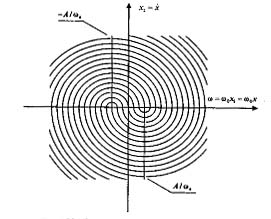
Рис. 4.20 - Фазовый портрет следящей системы при учете сил сухого трения

Уравнением линии переключения является х₂ = = 0.
Выше этой линии фазовые траектории представляют собой полуокружности радиуса , (d- любое число), проведенные относительно точки минус ; ниже этой линии - полуокружности с центром в точке .
Из рис. 4.20 видно, что сухое трение стабилизирует систему, превращая ее в устойчивую. Когда |ω| становится меньше , процессы заканчиваются, появляется зона нечувствительности.

4.5 Гармоническая линеаризация

В связи с трудностью точного исследования нелинейных систем выше третьего порядка большое значение имеют приближенные методы, хорошо зарекомендовавшие себя на практике Для систем, близких к линейным, часто применяется так называемый метод малого параметра, основанный на разложении неизвестных элементов движения системы в степенные ряды относительно малого параметра. Если совокупность нелинейных членов в дифференциальных уравнениях системы мала по сравнению с каждым из линейных членов, то этот метод дает хорошие результаты. Малым параметром в этом случае является искусственно вводимый или естественно присутствующий в уравнениях системы общий постоянный множитель всех нелинейных членов. Однако наиболее мощным и вследствие этого наиболее распространенным приближенным методом исследования нелинейных систем является метод гармонической линеаризации. Поэтому ограничимся изложением только этого метода.
Методом гармонической линеаризации можно относительно просто и с достаточной точностью исследовать многие типы стационарных нелинейных систем. Он позволяет оценивать устойчивость нелинейных систем, определять амплитуду и частоту автоколебаний, а также выбирать корректирующие звенья, обеспечивающие желаемые характеристики нелинейных систем.
Применение метода гармонической линеаризации предполагает существование в системе сигнала, близкого к синусоидальному, на основании чего осуществляется гармоническая линеаризация характеристик нелинейных звеньев.
Рассмотрим действие на нелинейное звено сигнала в виде синусоидальных колебаний, с постоянной амплитудой а:
х=asinωt . (4.37)
Выходной сигнал нелинейного звена, характеристика которого имеет вид (4.1), в этом случае также будет периодическим, но при гармонических колебаниях входной переменной х колебания выходной переменной у нелинейного звена уже не будут гармоническими.
Известно, что любая периодическая функция может быть разложена в ряд Фурье, поэтому выходной сигнал нелинейного звена при синусоидальном входном сигнале может быть представлен формулой:

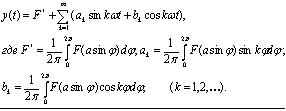
Величина F* представляет собой постоянную составляющую или среднее значение выходного сигнала у. Амплитуды a_k и b_k гармонических составляющих выходного сигнала у быстро уменьшаются с увеличением номера составляющей. Таким образом, в отличие от линейных звеньев, нелинейные звенья реагируют на гармонические колебания одной определенной частоты гармоническими колебаниями разных частот (теоретически - это бесконечная последовательность частот). В сумме эти гармонические колебания дают негармонические колебания выходного сигнала.
В САУ нелинейное звено практически всегда включается последовательно с линейными частями системы. Линейная часть, как правило, является фильтром низких частот и подавляет высокочастотные колебания. Поэтому имеются основания пренебречь гармониками выше первой на выходе нелинейного звена. Тогда, с учетом (4.37), получим приближенную линейную зависимость выходной переменной нелинейного звена от его входной переменной:

Таким образом, под действием гармонических колебаний нелинейное звено как бы линеаризуется и может рассматриваться приближенно как линейное звено. Коэффициенты q и q' называются гармоническими коэффициентами усиления нелинейного звена. Из формул для коэффициентов видно, что F*, q и q' зависят от амплитуды входного сигнала а. Эта зависимость отражает нелинейные свойства звена и из-за нее принцип суперпозиции (1.1) неприменим для гармонически линеаризованного нелинейного звена. Приближенное представление нелинейной зависимости y = F(x) при синусоидальном входном сигнале линейной зависимостью (4.38) называется гармонической линеаризацией. А основанный на этом приеме метод исследования нелинейных систем называется методом гармонической линеаризации или методом гармонического баланса (основы метода заложены Н.М. Крыловым и Н.Н. Боголюбовым, а в применении к автоматическим системам он иногда называется методом Л.С. Гольдфарба).
Отметим, что для любой нечетной характеристики F функция F* равна нулю, а для любой однозначной характеристики F второй коэффициент q' равен нулю (это соответствует отсутствию сдвига фаз между первой гармоникой на выходе нелинейного звена и входным синусоидальным сигналом):
Выражение (4.38) можно также представить в виде

(4.39)
где
(4.40)
Величина с характеризует усиление амплитуды, а ψ-сдвиг фазы гармонических колебаний нелинейного звена. Отметим, что в отличие от линейных систем усиление амплитуды и сдвиг фазы гармонически линеаризованным нелинейным звеном зависят от амплитуды входного сигнала. Запишем гармонический входной сигнал в комплексной форме: х=aе^iωt. Тогда первая гармоника выходного сигнала примет вид:
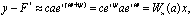(4.41)
где W_н(a)=се^iψ - комплексный гармонический коэффициент усиления (или амплитудно-фазовая характеристика, гармонический коэффициент передачи, описывающая функция) нелинейного звена.
Используя (4.40) и (4.41), получим для комплексного гармонического коэффициента усиления другое выражение:
W_н(a) = q(a) + iq'(a).
Комплексный гармонический коэффициент усиления безынерционного нелинейного звена (или его АФХ) не зависит от частоты, но зависит от амплитуды гармонических колебаний. В этом состоит основное отличие нелинейного безынерционного звена от линейного инерционного.
Для линейного звена АФХ не зависит от амплитуды, но зависит от частоты входных гармонических колебаний.

4.5.1 Гармонические коэффициенты усиления некоторых типовых нелинейных звеньев

Характеристики F(x) нелинейных звеньев делятся на две основные группы - однозначные и неоднозначные.
Рассмотрим для примера нелинейные звенья с однозначными характеристиками. Для таких звеньев q' ≡ 0, так как при гармоническом воздействии основная гармоника выходных колебаний нелинейных элементов совпадает по фазе с выходной величиной.
Ограничимся рассмотрением нелинейных звеньев с симметричной характеристикой относительно начала координат. Для таких характеристик F(x) - нечетная функция.
В качестве примера рассмотрим кусочно-линейную характеристику 1, показанную на рис. 1.11, в:

На характеристике у = F(x) можно указать три зоны:
1) зона нечувствительности |х| ≤ d;
2) зона линейности d < x < c;
3) зона насыщения |х| > |с|.
Прежде чем приступить к определению q, построим вспомогательный рис. 4.21. Кривая на рис.4.21 изображает изменение входной величины нелинейного звена х = asinωt = asinφ, а ломаная - изменение выходной величины у.

Рис. 4.21 - Расчет гармонических коэффициентов

От момента времени t = 0 до того момента, когда х станет равным d, выходная величина у = 0. В этот момент фазовый угол φ₁ определяется из равенства d = asinφ₁:
φ₁ = arcsin(d/a) (4.43)
Начиная с момента ωt₁ = φ₁ до момента ωt₂ = φ₂, где φ₂ определяется из равенства с = asinφ₂:
φ₂ = arcsin(c/a) (4.44)
выходная величина у линейно зависит от х:
у = γ(x - d) = γ(аsinφ - asinφ₁) = γа(sinφ - sinφ₁).
На участке φ₂ < φ < π - φ₂ выходная величина у = 1, а на участке π - φ₂ < φ < π - φ₁, опять зависит линейно от х.
Учитывая то, что в пределах 0 < φ < φ₁, подынтегральная Функция тождественно равна нулю, а также учитывая симметричность кривой у относительно прямых ωt = π/2 и ωt = 3π/2, выражение для q (см. (4.38)) представим в следующем виде:
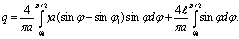(4.45)
Взяв интегралы и учитывая уравнения (4.42) - (4.44), получим:

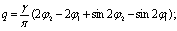
Из этой формулы вытекают следующие частные случаи:
а) имеет место насыщение, но зона нечувствительности отсутствует
б) есть зона нечувствительности, но насыщение отсутствует
в) идеальное двухпозиционное реле (d = с = 0, φ₂ = φ₁ = 0), для которого первый интеграл в (4.45) исчезает и q = 4l/πа.
Если однозначная нелинейность несимметрична, то появляется постоянная составляющая.
В качестве примера рассмотрим идеальный выпрямитель, характеристика которого имеет вид:

Если на вход действует гармоническое возмущение x=asinωt, то

и первая гармоника выходного колебания равна:

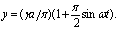
В данном случае несимметрия характеристик обусловлена физическими свойствами самого нелинейного звена. Другой причиной появления несимметричности характеристик нелинейного звена может быть наличие постоянной составляющей на входе:

Если характеристика F(x) неоднозначна и образует петли, то выходное колебание сдвигается по фазе и появляется комплексная составляющая гармонического коэффициента передачи пропорциональная площади петли. В качестве примера нелинейного звена с неоднозначной характеристикой рассмотрим двухпозиционное реле с зоной нечувствительности (рис.4.22).

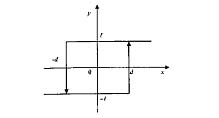
Рис. 4.22 - Рылейная характеристика с зоной нечувствительности

На входе звена действует сигнал: .
В этом случае F* = 0, а интеграл для вычисления коэффициента q должен быть записан в виде:

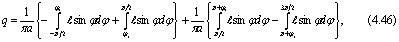
где первые два интеграла соответствуют ветви кривой функции F Для случая возрастания sinφ , вторые два интеграла соответствуют ветви кривой F для случая убывания sinφ,
Вычислив интегралы (4.46), получим
(4.47)
Для коэффициента q' имеем:

Вычислив эти интегралы, получим
(4.48)

4.5.2 Приближенное исследование стационарных нелинейных систем

Возможность применения метода гармонической линеаризации к стационарным нелинейным системам в основном определяется близостью периодического движения системы к синусоидальному. Это условие обычно удовлетворяется в случае, когда линейные части системы являются фильтрами низких частот. В качестве примера рассмотрим применение метода гармонической линеаризации для системы с одним нелинейным звеном с характеристикой F и линейной частью с передаточной функцией W(p) (рис. 4.23).

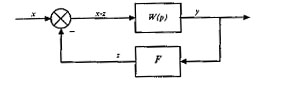
Рис. 4.23 - Одноконтурная нелинейная САУ

Предполагаем, что в нелинейной системе имеются смещенные автоколебания при x ≡ 0, поэтому представим все переменные в виде суммы постоянных составляющих и синусоидальных слагаемых с неизвестными амплитудой, частотой и начальной фазой одного из них:
y = у*+а_ysinω₀t, z = z*+ a_z sin (ω₀t + ψ_z). (4.49)
Проведем гармоническую линеаризацию нелинейного звена, т.е. зависимость z = F(y) заменим приближенной зависимостью:
z = F* + qy + (q'/ω₀) или z = F*(a_y,y*) + W_н(a_y,y*)y.
Последнюю формулу перепишем в следующем виде:
z = F*(a_y,y*) + |W_н(a_y,y*)|a_ysin(ω₀t + ψ_н), (4.50)
где W_н(аy,y) - комплексный гармонический коэффициент усиления, ψ_н = argW_н(a_y, y*).
Выходную переменную у линейной части системы на основе принципа суперпозиции (1.1) можно представить через переменную z в следующем виде:
у = -W(0)z* -|W(iω₀)|a_zsin[ω₀t + ψ_z+ ψ( ω₀)]. (4.51)
Из равенства правых частей формул (4.49) и (4.50) для z и в формулах (4.49) и (4.51) для у получим:
z* +a_zsin(ω₀t + ψ_z) = F*(a_y, y*)+|W_н(a_y, y*)|a_ysin(ω₀t + ψ), (4.52)
у*+аysinω₀t = -W(0)z* -|W(iω₀)|аz sin[ω₀t + ψ_z + ψ(ω₀)]. (4.53)
Сравнивая в правых и левых частях уравнений (4.52) и (4.53) постоянные составляющие, амплитуды и фазы синусоидальных составляющих, получим уравнения:

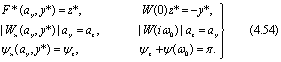
Исключая из уравнений (4.54) переменные a_z, z*, ψ_z, получим три уравнения для определения искомых переменных y*, a_y, ψ₀:
y*= -W(0)F*(a_y,y*), (4.55)
|W(iψ₀)|•|W_н(a_y, y*)| = 1, (4.56)
argW(iψ₀) + argW_н(a_y, y*) =iπ. (4.57)
Получить аналитическое решение уравнений (4.55)-(4.57) в общем виде невозможно. Для их решения применяются различные приближенные методы.
Удобно также воспользоваться графическими способами.
Рассмотрим возможные способы графического решения этой системы уравнений.
Первый способ состоит в следующем. На координатной плоскости 0у*а_y (рис.4.24) по уравнению (4.55) построим кривую 1. Затем при определенных значениях ω₀ задаемся значениями у* и определяем из уравнений (4.56) и (4.57) соответствующие значения а_y.

Рис. 4.24 - Графическое решение уравнений (4.54)

По результатам этих вычислений для различных конкретных значений ω₀ строим кривые 2, соответствующие уравнению (4.56), и кривые 3, соответствующие уравнению (4.57). Точка пересечения кривых 2 и 3 на рис. 4.24 является совместным решением уравнений (4.56) и (4.57) для конкретного значения ω₀.
Построив кривые 2 и 3 для ряда значений ω₀, соединим точки их пересечения кривой 4. Точка пересечения кривой 4 и кривой 1 определяет искомые значения у* и a_y, удовлетворяющие всем трем уравнениям (4.55), (4.56) и (4.57). Для определения частоты автоколебаний ω₀ следует подставить найденные значения у* и a_y в уравнение (4.56) или в уравнение (4.57).
Частоту автоколебаний можно также определить по шкале значений ω₀, полученной на кривой 4 (рис. 4.24) при ее построении по достаточно большому числу точек. Однако этот способ менее точен, чем предыдущий.
Второй способ отличается от первого способа только приемом отыскания кривой 4 для рис. 4.24.
Объединим уравнения (4.56) и (4.57) в одно уравнение
W(iω₀)W_н(a_y,y*) = -1 (4.58)
и перепишем его в виде :
W(iω₀) = -1/W_н(a_y,y*). (4.59)
Построим на комплексной плоскости (рис. 4.25) АФХ линейной части системы W(iω) и обратную АФХ нелинейного звена со знаком "-", т.е. -1/W_н(a_y,y*) для разных значений y* при изменении ω₀ и а_y от 0 до ∞.

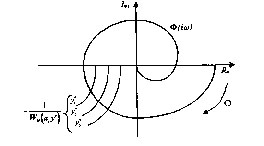
Рис. 4.25 - Графическое решение уравнения (4.59)

Точки пересечения этих характеристик определяют зависимость ау=f(y*), соответствующую уравнению (4.59), т.е. кривую 4 для рис.4.24. Далее определяем на рис. 4.24 точку ее пересечения с кривой 1, построенной по уравнению (4.55). Определяем ω₀ аналогично первому способу.
Для совместного решения уравнений (4.55) - (4.57) используются также ЛЧХ.
Если не существует действительных значений у* и положительных значений а_y и ω₀, удовлетворяющих уравнениям (4.55)-(4.57), то автоколебания в системе невозможны.
После определения путем решения уравнений (4.55)-(4.57) параметров периодического движения системы необходимо оценить устойчивость этого движения, что подтвердит его соответствие реально существующим в системе автоколебаниям. Особенно важно это проверить при наличии нескольких периодических решений.
Для исследования устойчивости периодического движения системы можно применить первый метод Ляпунова, т.е. составить соответствующие уравнения в вариациях и исследовать устойчивость определенной ими линеаризованной системы.
Приближенно оценить устойчивость автоколебаний можно на основе следующих рассуждений.
Движение системы, близкое к найденному периодическому, можно приближенно считать синусоидальным с медленно изменяющейся амплитудой А, приближающейся к амплитуде автоколебаний а_у. в случае устойчивых автоколебаний и удаляющейся от а_у в случае неустойчивых автоколебаний.
Если автоколебания в системе устойчивы и имеют амплитуду a_y, то при замене ее в уравнении (4.58) величиной А > a_y пара чисто мнимых корней ±iω₀ должна замениться парой комплексных сопряженных корней с отрицательной действительной частью, а при замене а_у величиной А < a_y корни ±iω₀ должны замениться парой комплексных сопряженных корней с положительной действительной частью.
Для проверки характера изменения корней ±iω₀ при замене в уравнении (4.58) величины a_y величиной А удобно использовать критерий Найквиста.
Так как уравнение (4.58) имеет чисто мнимые корни ±iω₀ при А=ау, то АФХ разомкнутой системы
Wp (iω₀,a_y,y) = W(iω)W_н(u,y*) (4.60)
при А = a_y проходит через точку минус 1 плоскости комплексной переменной (рис. 4.26 - кривая 1).

Рис. 4.26 - Проверка устойчивости автоколебаний

В случае неустойчивых автоколебаний должна наблюдаться обратная картина.
В случае полуустойчивого предельного цикла кривая (4.60) смещается в одну и ту же сторону при А > a_yи при А < a_y.

4.6 Качество переходных процессов и коррекция нелинейных САУ

В нелинейных САУ качество переходных процессов принято оценивать теми же показателями, что и в линейных системах: временем переходного процесса t_п максимальным отклонением и колебательностью. Но в нелинейных САУ эти показатели зависят от величины внешнего воздействия, породившего переходный процесс.
Анализ показателей качества переходных процессов в нелинейных системах начнем с наиболее простого случая, когда предполагается, что входящие в систему нелинейности не оказывают существенного влияния на динамику системы. В этом случае в первом приближении можно исследовать качество переходных процессов и построить сам процесс без учета всех нелинейностей, т.е. исследовать систему как линейную. Такое исследование возможно, например, для непрерывных САУ с насыщением, небольшой зоной нечувствительности, неоднозначной характеристикой с достаточно узкой петлей и т.д. (см. пример в подразделе 4.2). После проведения приближенного исследования оценивается влияние на динамику САУ неучтенных нелинейностей. Если проводился приближенный синтез системы, то после этого при необходимости проводится дополнительная коррекция. Осуществляется также построение переходных процессов с учетом исключенных нелинейностей. Для этого используются методы численного интегрирования и ЭВМ.
Для приближенной оценки влияния нелинейностей используется метод гармонической линеаризации. Нелинейное звено заменяется гармонически линеаризованным звеном и предполагается, что его комплексный гармонический коэффициент усиления W_н(а) справедлив и для случая произвольной формы входного сигнала х. Формально это выражается заменой в W_н(a) величины а на x. Выразив таким образом параметры комплексного гармонического коэффициента усиления через входной сигнал х и определив зависимость качества переходных процессов в линейной системе от значений этих параметров, можно приближенно оценить влияние нелинейности звена на переходные процессы. Например, для звена с насыщением эта методика предлагает замену эквивалентным звеном, гармонический коэффициент передачи которого уменьшается с ростом входного сигнала х так же, как гармонический коэффициент передачи этого звена уменьшается с увеличением амплитуды а входных колебаний. Для оценки быстродействия в гармонически линеаризованной системе применяется показатель колебательности М и полоса пропускания. В отличие от линейных систем здесь вместо одной частотной характеристики строится серия таких характеристик в зависимости от амплитуды а. Соответственно и качество переходных процессов будет зависеть от величины отклонения от установившегося режима.
Для нелинейных систем второго порядка качество переходных процессов полностью определяется по фазовому портрету системы. Для нелинейных систем, устойчивость которых исследовалась с помощью второго (прямого) метода Ляпунова или критерия абсолютной устойчивости В.М. Попова длительность переходных процессов можно оценить с помощью этих же методов на основе понятия степени устойчивости η (см. подраздел 3.4).
Предположим, что у нас есть возможность определить максимальное значение η, при котором для всех возможных процессов x(t) в нелинейной системе выражение х(t)е^ηt ⊾ 0 при t ⊾ ∞, а при бесконечно малом превышении этого значения η это условие уже не выполняется. Это значит, что переходные процессы в системе затухают не медленнее, чем экспонента e^-ηt. Следовательно, найденная величина ηt может служить оценкой сверху длительности t_п переходных процессов в системе, т.е. .
Так как в линейной системе переходный процесс может быть представлен в виде суммы , где λ_i- корни характеристического уравнения, умножение x(t) на e^ηt эквивалентно в рассматриваемом случае уменьшению на η действительных корней характеристического уравнения. Т.е. здесь использованное понятие степени устойчивости для линейных систем совпадает с уже известной нам степенью устойчивости η, представляющей собой величину минимальной действительной части корней характеристического уравнения системы (см. (3.60) в подразделе 3.4).
В общем случае нелинейной системы для нахождения величины степени устойчивости η также можно использовать существующие критерии устойчивости нелинейных систем, в частности прямой метод Ляпунова и критерий абсолютной устойчивости В.М. Попова.
Для этого необходимо предварительно в уравнении системы произвести замену переменной x(t) на х(t)^ηt.
Соответственно при применении критерия абсолютной устойчивости В.М. Попова условием наличия у системы степени устойчивости не менее η является выполнение этого критерия для характеристики вместо (см. подраздел 4.3).
Как и в линейных САУ, при анализе качества нелинейных систем находят величину η, как значение неизвестного параметра, при котором для измененного уравнения система оказывается на границе устойчивости. При синтезе системы могут быть построены линии равных значений η внутри области устойчивости системы в плоскости каких-либо варьируемых параметров. Граница области устойчивости соответствует η = 0.
Рассмотрим возможность определения степени устойчивости η с помощью гармонической линеаризации. Этот метод можно применить для исследования не только гармонических колебаний, но и колебательных переходных процессов. При этом гармоническая линеаризация осуществляется для сигнала на входе нелинейного звена в виде
x(t)=x₀(t)+ae^-ηtsinωt. (4.61)
Коэффициенты гармонически линеаризованного уравнения
нелинейного звена получаются в виде функций неизвестных параметров х₀, а, ω и η искомого решения (4.61). Т.е. в результате исследования определяются перечисленные параметры, включая и величину степени устойчивости η, определяющую время переходного процесса. При синтезе САУ аналогично может быть найдена зависимость η от варьируемых параметров системы, например построением линий постоянных значений η в плоскости этих параметров. Методика здесь та же, что и для определения степени устойчивости линейных САУ, с той только разницей, что применяется она к предварительно линеаризованной системе.
Рассмотрим особенности коррекции динамических свойств нелинейных САУ.
Как и в линейных САУ, коррекция динамических свойств нелинейных систем осуществляется с помощью последовательных и параллельных КЗ. Эти звенья могут быть линейными и нелинейными Линейные КЗ были рассмотрены в подразделе 3.5. Все изложенное выше о них в полной мере справедливо и в случае применения этих звеньев для коррекции нелинейных САУ.
Рассмотрим принципиально новые возможности, возникающие при применении нелинейных звеньев с целью коррекции динамических свойств системы.
Наиболее очевидно эффективное использование нелинейных КЗ для устранения или уменьшения отрицательного влияния на работу системы какой-либо входящей в нее нежелательной нелинейности.
Например, с помощью звена со специально подобранной нелинейной характеристикой может быть изменена статическая характеристика всей САУ в целом. Другой пример - уменьшение влияния насыщения, которое приводит к увеличению длительности переходных процессов, т.е. к снижению быстродействия системы при больших внешних воздействиях. В таких случаях можно добиться значительного ускорения переходных процессов, если линейные КЗ, создающие форсирующее воздействие, заменить или дополнить нелинейными звеньями, которые затягивали бы форсировку, задерживая сигнал на предельно возможном с учетом насыщения значении.
В шестом разделе будет показано, что для получения максимального быстродействия при наличии ограничений на переменные управление должно быть релейным, т.е. нелинейным.
Нелинейная коррекция является более общим средством по сравнению с линейной коррекцией и позволяет повышать качество в том числе и линейных САУ с получением результатов, недостижимых для линейной коррекции.
Например, с помощью нелинейной коррекции в чисто линейной САУ можно устранить известное противоречие между быстро-действием и колебательностью, обеспечив возможность независимого выполнения требований по каждому из этих показателей.
Если в линейной САУ для повышения быстродействия увеличивать коэффициент передачи разомкнутой системы, то предел этому создает возрастающая в конце концов колебательность переходного процесса.
Линейная коррекция позволяет повысить максимально достижимое при этом значение коэффициента передачи, однако принципиально не решает отмеченного противоречия, требующего компромиссного решения при выборе коэффициента передачи и самой коррекции (см. подраздел 3.5).
Это наглядно иллюстрирует рис. 4.27, где приведены переходные характеристики 1, 2 и 3 линейной САУ для трех линейных КЗ, дающих все возрастающую форсировку процесса.

Рис. 4.27 - Переходная характеристика системы при нелинейной коррекции

Противоречие можно устранить, если изменять коррекцию в ходе переходного процесса так, чтобы в первой его части коррекция определялась только по условию обеспечения требования к быстродействию, а затем изменялась на основе требования к устойчивости и колебательности процесса. При этом коррекция, выбранная для первой части переходного процесса, будет настолько сильной, что если ее не изменять к концу, переходный процесс получится с очень большой колебательностью, вплоть до неустойчивости.
Подобное изменение коррекции в ходе переходного процесса означает переход к нелинейной коррекции (см. рис. 4.4), так как сводится к изменению структурной схемы или параметров КЗ в функции переменных величин, характеризующих процессы в системе. При больших отклонениях от установившегося режима, соответствующих началу переходного процесса, коррекция обеспечивает максимально быстрое устранение этого отклонения, а затем, когда отклонение снижено до достаточно малой величины, коррекция обеспечивает неколебательное окончание переходного процесса.
Такая нелинейная коррекция реализуется либо с помощью реле, осуществляющего переключение с одного КЗ на другое в функции выходной величины системы или какой-либо другой переменной, либо с помощью нелинейных звеньев со специально подобранной характеристикой, включенных последовательно с линейными КЗ и изменяющих коэффициент передачи в ходе переходного процесса.
Например, требуемая форсировка при больших отклонениях от установившегося состояния может быть получена включением последовательно в прямой канал САУ или в каналы форсирующих корректирующих воздействий нелинейного звена с характеристикой, приведенной на рис. 4.28, или введением нелинейного звена с выпуклой характеристикой типа характеристики с насыщением в цепь отрицательной обратной связи или в цепь корректирующих воздействий, изменяющих (демпфирующих) переходный процесс.

Рис. 4.28 - Статическая характеристика нелинейного К3

Так может быть получен процесс, изображенный на рис. 4.27 сплошной линией. Начальная часть процесса совпадает с переходной характеристикой 3 линейной системы, а далее происходит увеличение демпфирования и процесс переходит в установившееся состояние согласно характеристике 1. Изложенное показывает большие возможности нелинейной коррекции.
Отмечая достоинства нелинейной коррекции, в частности в линейных системах, что она по своей природе является более специализированной по отношению к режимам работы системы, в которых выдает нужный эффект.
Может получится, например, так, что нелинейная коррекция, выбранная для определенного вида внешних воздействий, окажется не только не эффективной, но даже вредной для других неучтенных режимов САУ.
Поэтому, чем шире диапазон внешних воздействий и вообще условий работы системы, тем труднее выбрать нелинейную коррекцию.
К сожалению, общей методики выбора нелинейных КЗ несуществует и практически при синтезе используется метод проб и последовательных приближений, а также опыт и нестрогие рекомендации по применению отдельных частных приемов и схем нелинейной коррекции, описанные в учебной и справочной литературе.

Контрольные вопросы

 

1. Особенности поведения нелинейых систем.
2. Основные виды нелинейностей.
3. Динамические нелинейности.
4. Сухое трение.
5. Нелинейная коррекция.
6. Нелинейная логика.
7. Нелинейные законы управления.
8. Особенности математического описания нелинейных систем.
9. Способы линеаризации непрерывных слабых нелинейностей.
10. Особенности линеаризации нестационарных систем.
11. Устойчивость нелинейных систем.
12. Особенности определения условий устойчивости.
13. Определения устойчивости по Ляпунову.
14. Первый метод Ляпунова.
15. Второй (прямой) метод Ляпунова.
16. Функции Ляпунова.
17. Критерий абсолютной устойчивости В.М. Попова.
18. Развитие исследований по проблеме Айзермана.
19. Метод точечных преобразований (отображений).
20. Исследование следящей системы методом точечных преобразований.
21. Гармоническая линеаризация нелинейностей.
22. Расчет гармонических коэффициентов.
23. Приближенное исследование стационарных нелинейных систем методом гармонической линеаризации.
24. Оценка качества переходных процессов в нелинейных САУ.
25. Особенности коррекции динамики нелинейных САУ. Примеры нелинейных КЗ.

---

Дата добавления: 2021-04-15; просмотров: 308; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!