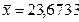Обработка результатов измерений
Критерий Романовского
Критерий Романовского применяется, если число измерений n < 20. При этом вычисляется отношение
(1.1)
xi – проверяемое значение (наименьший/наибольший результат измерения); 
– среднее арифметическое значение измеряемой величины; Sx – среднее квадратическое отклонение (СКО).
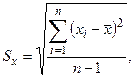(1.2)
n – количество измерений.
В зависимости от выбранного уровня значимости, т. е. от желания экспериментатора получить уверенный результат проверки гипотезы, и числа измерений n из таблицы 1.1 находят теоретический критерий Романовского bт, и сравнивают с ним расчетное значение b. Если b ³ bт, то результат xi считается промахом и отбрасывается.
Таблица 1.1
Значения критерия Романовского b т = f ( n )
| q | n = 4 | n = 6 | n = 8 | n = 10 | n = 12 | n = 15 | n = 20 |
| 0 ,01 | 1,73 | 2,16 | 2,43 | 2,62 | 2,75 | 2,90 | 3,08 |
| 0,02 | 1,72 | 2,13 | 2,37 | 2,54 | 2,66 | 2,80 | 2,96 |
| 0,05 | 1,71 | 2,10 | 2,27 | 2,41 | 2,52 | 2,64 | 2,78 |
| 0,10 | 1,69 | 2,00 | 2,17 | 2,29 | 2,39 | 2,49 | 2,62 |
Пример решения
При шестикратном измерении расстояний между ориентирами осей зданий получены следующие результаты:
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| xi, м | 25,155 | 25,150 | 25,165 | 25,165 | 25,160 | 25,180 |
Последний результат вызывает сомнения. Произведем проверку по критерию Романовского, не является ли он промахом?
Находим среднее арифметическое значение:
|
|
|
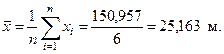
По формуле (1.2) определяем среднее квадратическое отклонение. Для удобства вычислений составим таблицу 1.2.
Оценка СКО:
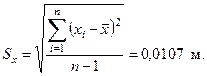
Таблица 1.2
Обработка результатов измерений
| № п/п | xi |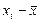 
| 
|
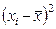
| 1 | 25,155 | -0,008 | 0,000064 |
| 2 | 25,15 | -0,013 | 0,000169 |
| 3 | 25,165 | 0,002 | 0,000004 |
| 4 | 25,165 | 0,002 | 0,000004 |
| 5 | 25,16 | -0,003 | 0,000009 |
| 6 | 25,18 | 0,017 | 0,000289 |
| 
|
Вычисляем b для сомнительного результата измерения (при n = 6)
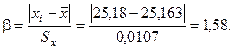
Выводы: критическое значение b при уровне значимости q = 0,05 для количества измерений n = 6 составляет 2,1. Поскольку 1,58 < 2,1 (b < bт), результат не является промахом и не исключается из результатов измерений.
Критерий Шарлье
Критерий Шарлье используется, если число измерений велико (n > 20). Тогда по теореме Бернулли число результатов, превышающих по абсолютного значению среднее арифметическое значение на величину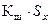 
, будет 
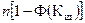, где 
- значение нормированной функции Лапласа для X = Kш.
Если сомнительным в ряду результатов наблюдений является один результат, то
.
Отсюда
.
Значения критерия Шарлье приведены в таблице 1.3.
Таблица 1.3
Значения критерия Шарлье
| n | 5 | 10 | 20 | 30 | 40 | 50 | 100 |
| Kш | 1,3 | 1,65 | 1,96 | 2,13 | 2,24 | 2,32 | 2,58 |
|
|
|
Пользуясь данным критерием, отбрасывается результат, для значения которого выполняется неравенство [1]
.
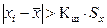Пример решения
При измерении расстояний между колоннами были получены следующие результаты (таблица 1.4, значения xi).
Таблица 1.4
Обработка исходных данных
| № п/п | xi |
|
| Проверка по критерию Шарлье | ||
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 2 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
| 3 | 23,66 | -0,01 | 0,0001 | не является промахом | ||
| 4 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 5 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 6 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
| 7 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 8 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
| 9 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 10 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
| 11 | 23,66 | -0,01 | 0,0001 | не является промахом | ||
| 12 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 13 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 14 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
| 15 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
| 16 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
| 17 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 18 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
| 19 | 23,68 | 0,01
| 0,0001 | не является промахом | ||
| 20 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 21 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
| 22 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 23 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 24 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 25 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
| 26 | 23,66 | -0,01 | 0,0001 | не является промахом | ||
| 27 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
| 28 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 29 | 23,67 | 0,00 | 0,0000 | не является промахом | ||
| 30 | 23,68 | 0,01 | 0,0001 | не является промахом | ||
|
|
| 
|
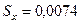
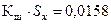
Обработка результатов измерений
Находим СКО:
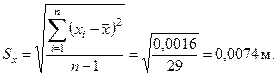
Проверяем ряд измерений на наличие промаха. Если условие 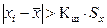выполняется, то результат измерения xi отбрасывается.
Критерий Шарлье для числа измерений n = 30
Kш = 2,13.
Таким образом, проверяемые значения не являются промахом (см. табл. 1.4) и не отбрасываются из ряда измерений.
Критерий Диксона
Вариационный критерий Диксона удобный и достаточно мощный (с малыми вероятностями ошибок). При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд 
. Критерий Диксона определяется как
.
Критическая область для этого критерия 
. Значения Zq приведены в таблице 1.5.
|
|
|
Таблица 1.5
Значения критерия Диксона
| n | Zq при q , равном | |||
| 0,10 | 0,05 | 0,02 | 0,01 | |
| 4 | 0,68 | 0,76 | 0,85 | 0,89 |
| 5 | 0,56 | 0,64 | 0,78 | 0,82 |
| 6 | 0,48 | 0,56 | 0,64 | 0,70 |
| 8 | 0,40 | 0,47 | 0,54 | 0,59 |
| 10 | 0,35 | 0,41 | 0,48 | 0,53 |
| 14 | 0,29 | 0,35 | 0,41 | 0,45 |
| 16 | 0,28 | 0,33 | 0,39 | 0,43 |
| 18 | 0,26 | 0,31 | 0,37 | 0,41 |
| 20 | 0,26 | 0,30 | 0,36 | 0,39 |
| 30 | 0,22 | 0,26 | 0,31 | 0,34 |
Пример решения
Было проведено пять измерений напряжения в электросети. Получены следующие данные:
| i | 1 | 2 | 3 | 4 | 5 |
| xi, В | 127,1 | 127,2 | 126,9 | 127,6 | 127,2 |
Результат 127,6 В существенно (на первый взгляд) отличается от остальных. Необходимо проверить, не является ли он промахом.
Составим вариационный ряд из результатов измерений напряжения в электросети:
| i | 1 | 2 | 3 | 4 | 5 |
| xi, В | 126,9 | 127,1 | 127,2 | 127,2 | 127,6 |
Для крайнего члена этого ряда (127,6) критерий Диксона
.
Как следует из таблицы 1.5, по этому критерию результат 127,6 В может быть отброшен как промах лишь на уровне значимости q = 0,10.
Задание 2. Статистическая обработка многократных измерений.
Статистическая обработка группы результатов наблюдения при равноточных измерениях, нормальном распределении, выполняется в следующей последовательности.
1. Производится n измерений х i величины х.
2. Вычисляем среднее арифметическое значение 
, принимая его за оценку истинного значения измеряемой величины:
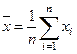. (2.1)
3. Вычисляем отклонения каждого результата измерения относительно среднего арифметического (абсолютную погрешность):
.
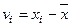4. Вычисляем среднеквадратическое отклонение среднего арифметического значения:
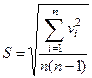. (2.2)
5. Задается доверительная вероятность Рд.
6. Вычисляем размах доверительного интервала через коэффициент Стьюдента tnp:
. (2.3)
Коэффициент tnp выбирается из таблицы
Таблица 2.1
Дата добавления: 2021-07-19; просмотров: 501; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!