Задания для контрольных и самостоятельных работ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ
(образован в 1953 году)

Кафедра физики и высшей математики
| Физ.мат.-4.22.260602 зчн.плн. Физ.мат.-4.22.260602 зчн.скр. Физ.мат.-4.22.260601 зчн.плн. Физ.мат.-4.22.260601 зчн.скр. | Физ.мат.-4.22.220301зчн.плн Физ.мат.-4.22.220301 зчн.скр. Физ.мат.-4.22.140401 зчн.плн. Физ.мат.-4.22.140401 зчн.скр. |
К.В. Малакеева, К.В. Головко
Математика
Учебно-методическое пособие и контрольные задания для студентов-заочников I курса специальностей: 140401, 220301, 260601, 260602
Часть 2

Www . msta . ru
4894
Москва – 2005
УДК 17
ÓМалакеева К.В., Головко К.В. Математика. Методические указания и контрольные задания для студентов - заочников I курса специальностей 140401, 220301, 260601, 260602. Часть 2. М. МГУТУ 2005г.
Данное пособие предназначено для студентов механических специальностей заочного отделения МГУТУ. при соответствии программе курса акцент сделан на сообщении студентам сведений, необходимых для практического применения математического аппарата в профессиональной деятельности. Приведены необходимые графические иллюстрации и примеры решения типовых задач. По всем разделам приведены тесты и контрольные вопросы, помогающие студентам самостоятельно контролировать усвоение знаний. Пособие может быть рекомендовано другим специальностям высших учебных заведений.
Авторы: Малакеева К.В., Головко К.В.
Рецензенты: Зав. кафедрой «Теоретическая механика» МГТУ «МАМИ», академик РАЕН, д. ф.-м. н. проф. Бондарь В.С.;
Зав. кафедрой высшей математики Московского Государственного Текстильного Университета к. ф.-м. н., доцент Матвеев Е.М.;
К. ф-м. н., доцент МГТУ «МАМИ» Даншин В.В.
Редактор: Свешникова Н.И.
ÓМосковский государственный университет технологий и управления, 2005
109004, Москва, Земляной вал, 73
Содержание
| §3. Дифференциальное исчисление функций одной и нескольких переменных------------------------------------------------------------------------ | 4 |
| Тест 3------------------------------------------------------------------------------- | 27 |
| Задания для контрольных и самостоятельных работ--------------------- | 27 |
| §4. Интегрирование исчисление функций. Приложение определенных интегралов------------------------------------------------------ | 35 |
| Задания для контрольных и самостоятельных работ--------------------- | 52 |
| Тест 4------------------------------------------------------------------------------- | 56 |
| Ответы к тестам------------------------------------------------------------------ | 56 |
| Вопросы для самоконтроля---------------------------------------------------- | 57 |
| Приложения (основные математические формулы)---------------------- | 58 |
| Литература------------------------------------------------------------------------ | 65 |
§3 Дифференциальное исчисление функций одной и нескольких переменных.
Производной первого порядка (первой производной) непрерывной функции  в точке х называется предел отношения приращения функции
в точке х называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента 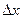 , когда последнее стремится к нулю:
, когда последнее стремится к нулю:
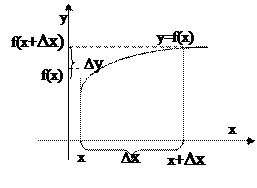
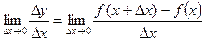
Если такой конечный предел в точке х существует, то функция называется дифференцируемой в точке х.
Обозначения производной: 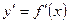 (Лагранж),
(Лагранж),  (Лейбниц),
(Лейбниц), 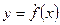 (Ньютон).
(Ньютон).
В тех случаях, когда неясно, по какому аргументу (х, t и т.п.) происходит дифференцирование функции у, для соответствующих производных употребляются обозначения 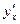 ,
, 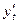 и т.п. Нахождение производной называют дифференцированием функции.
и т.п. Нахождение производной называют дифференцированием функции.
Значение производной функции  в точке
в точке 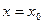 обозначают
обозначают 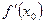 .
.
Дифференциалом dx независимой переменной х называют её приращение  .
.
Дифференциалом  называется
называется  .
.
Примечание: производная функции  есть некоторая функция
есть некоторая функция 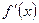 , произведенная (т.е. полученная по определенным правилам) из данной функции.
, произведенная (т.е. полученная по определенным правилам) из данной функции.
Касательной к графику функции y= f( x) в точке М( x0, y0) называют предельное положение секущей ММ1 при произвольном стремлении точки М1 к точке М (иначе:  ).
).
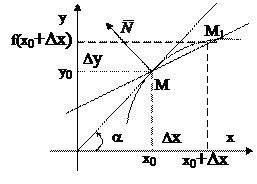
Уравнение касательной имеет вид: y- y0 = k( x- x0), где угловой коэффициент касательной 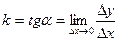 , т.е.
, т.е. 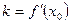 .
.
Угол a между положительным направлением оси Ох и касательной отсчитывают против часовой стрелки.
Если  , то касательная к графику непрерывной функции f( x) будет перпендикулярна оси Ох, уравнение такой касательной имеет вид х = х0.
, то касательная к графику непрерывной функции f( x) будет перпендикулярна оси Ох, уравнение такой касательной имеет вид х = х0.
Если 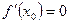 , то касательная параллельна оси Ох.
, то касательная параллельна оси Ох.
Уравнение нормали (перпендикуляр к касательной в точке М(х0,у0)  имеет вид:
имеет вид: 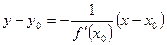 .
.
Если  , то уравнение нормали имеет вид у=у0.
, то уравнение нормали имеет вид у=у0.
Если 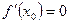 , то
, то  будет перпендикулярна оси Ох и ее уравнение будет у=х0.
будет перпендикулярна оси Ох и ее уравнение будет у=х0.
 Под углом между кривыми
Под углом между кривыми  и
и  в их общей точке М(х0,у0) понимается угол
в их общей точке М(х0,у0) понимается угол  , между касательными М0А и М0В к этим кривым в точке М0.
, между касательными М0А и М0В к этим кривым в точке М0.
По известной формуле аналитической геометрии получаем: 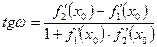 .
.
Замечание: если в точке х0 существует конечная производная, то функция непрерывна в этой точке. Обратное предложение не всегда справедливо.
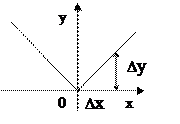 Например, функция
Например, функция 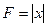 в точке х=0 непрерывна, т.к. приращение функции
в точке х=0 непрерывна, т.к. приращение функции  и в точке х=0
и в точке х=0  , стало быть, при
, стало быть, при  и
и 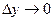 , а производной в этой точке функция не имеет. Убедимся в этом:
, а производной в этой точке функция не имеет. Убедимся в этом:
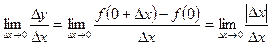 ,
,
 ,
, 
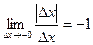 , т.е. и производной в этой точке функция не имеет.
, т.е. и производной в этой точке функция не имеет.
Если существуют односторонние пределы
 и
и 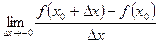 ,
,
не равные между собой, то говорят, что существуют односторонние производные функции в точке х0, а точку х0 называют угловой точкой графика функции. В приведенном примере односторонние производные (справа и слева) в точке х = 0 существуют.
Предположим, что точка М движется по некоторой прямой, которую примем за ось Ох. Каждому значению времени t соответствует определенное расстояние ОМ = х.
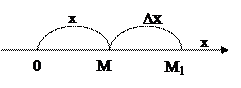 |
Следовательно, можно сказать, что абсцисса х движущейся точки есть функция времени t: х = f(t) – это уравнение называется уравнением движения, оно выражает закон движения точки.
Отношение  выражает среднюю скорость изменения абсциссы х за промежуток времени t.
выражает среднюю скорость изменения абсциссы х за промежуток времени t.
Скорость движения (мгновенная скорость) в данный момент времени t вычисляется непосредственно:
 .
.
Примеры:
1.Если s = s(t) – закон движения материальной точки, определяющий зависимость пути s от времени t, то производная  определяет мгновенную скорость материальной точки в момент времени t. Дифференциал
определяет мгновенную скорость материальной точки в момент времени t. Дифференциал 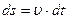 определяет путь, который прошла бы материальная точка, двигаясь равномерно с мгновенной скоростью
определяет путь, который прошла бы материальная точка, двигаясь равномерно с мгновенной скоростью 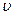 в момент времени t, за промежуток времени от момента t до (t + dt).
в момент времени t, за промежуток времени от момента t до (t + dt).
2.Если q = q(t) – закон, определяющий зависимость количества электричества, протекающего через поперечное сечение проводника, от времени t, то производная 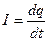 определяет силу тока в момент времени t. Дифференциал dq = I × dt определяет количество электричества, которое могло бы пройти через поперечное сечение проводника при постоянной силе тока I в момент времени t за промежуток времени dt.
определяет силу тока в момент времени t. Дифференциал dq = I × dt определяет количество электричества, которое могло бы пройти через поперечное сечение проводника при постоянной силе тока I в момент времени t за промежуток времени dt.
Замечание: именно рассмотрение задач о касательной и скорости движения исторически привело к понятию производной, являющейся одним из основных понятий высшей математики.
3.Пусть х = f(x) – закон, определяющий количество вещества, образовавшегося при химической реакции за промежуток времени t, тогда  - скорость химической реакции в данный момент времени t.
- скорость химической реакции в данный момент времени t.
Непосредственное нахождение производной можно осуществить, пользуясь определением, по следующей схеме:
1.дать аргументу х произвольное приращение 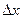 и найти соответствующее новое значение функции
и найти соответствующее новое значение функции  ;
;
2.определить приращение функции  ;
;
3.составить отношение 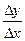 ;
;
4.найти предел 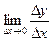
Пример: Точка движется по прямой, согласно закону s = 3t2 + 2t, где t – время в секундах, s – путь в метрах. Найти скорость точки в момент t = 3.
Решение:
1.  ;
;
2. 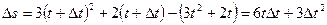 ;
;
3. 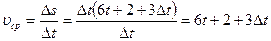 (средняя скорость за промежуток времени
(средняя скорость за промежуток времени  от t до
от t до 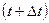 );
);
4. теперь найдем скорость в момент времени t = 3: 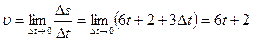 ., при t = 3
., при t = 3  (м/сек).
(м/сек).
Таблица основных элементарных функций, а также основные правила дифференцирования даны в Приложении 6.
Примеры:
1. Вычислить производные следующих функций:
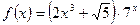 ,
,  .
.
Решение:
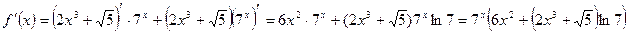

2. Вычислить значение производной функции
 в точке с абсциссой х0 = 1.
в точке с абсциссой х0 = 1.
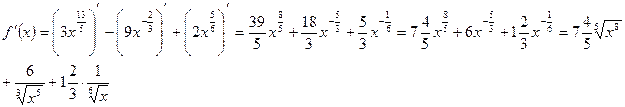
 .
.
3. Написать уравнение касательной к графику функции 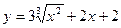 в точке с абсциссой х0 = -1.
в точке с абсциссой х0 = -1.
Ищем ординату точки касания: 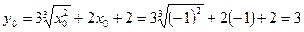 .
.
Угловой коэффициент касательной:
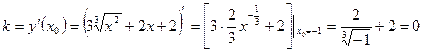 .
.
Подставив х0, у0 и k в уравнение касательной, получаем:
(у – 3) = 0(х + 1), откуда
у = 3
4. Какой угол образует с осью Ох касательная к кривой у = х – х2 в точке с абсциссой х = 0?
Найдем угловой коэффициент касательной: 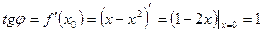 , следовательно
, следовательно  .
.
Пример: найти производные следующих функций:
1.  ;
;
2.  ;
;
3. 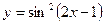 .
.
Решение: 1. Функция имеет вид у = u2, где  , значит
, значит  или
или 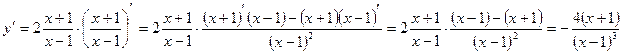
2.Функция имеет вид 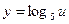 , где u = x3 – 1, следовательно,
, где u = x3 – 1, следовательно, 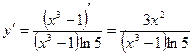 ;
;
3. Функция имеет вид: у = u2, где  , т.е.
, т.е.
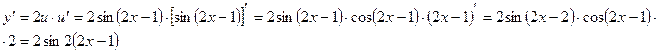 Пример: Вычислить производную функции
Пример: Вычислить производную функции  в точке
в точке 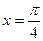 .
.
Решение: Здесь целесообразно сначала преобразовать функцию в правой части. Получим. 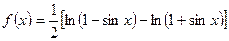 .
.
Теперь вычислим производную:  .
.
Полагая 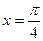 , найдем:
, найдем:  .
.
Логарифмической производной функции у = f(х) называется производная от логарифма этой функции, т.е.
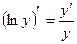
Нахождение производных от функций, которые допускают операцию логарифмирования (произведение, частное, возведение в степень и извлечение корня), значительно упрощается, если функции предварительно прологарифмировать.
Пример: Найти 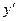 , если
, если 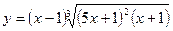 .
.
Решение: 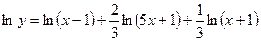 ;
;
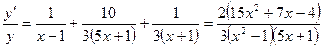 , отсюда
, отсюда
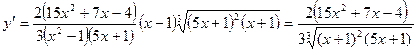 .
.
Чтобы найти производную от неявной функции, надо данное уравнение продифференцировать, считая у функцией от х, и вновь полученное уравнение решить относительно производной 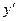 .
.
Пример:
1. 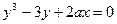
Дифференцируем обе части по х, считая у функцией от х: 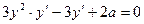 , отсюда
, отсюда 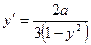 .
.
2. 
Дифференцируем обе части по х, считая у функцией от х: 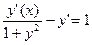 , отсюда
, отсюда 
Если для функции у = f(x) производная 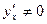 , то производная обратной функции
, то производная обратной функции 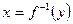 (см. § 2) есть
(см. § 2) есть 
Пример: Найти  , если у = х + lnх.
, если у = х + lnх.
Имеем 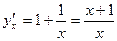 , следовательно,
, следовательно, 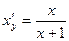 .
.
Если зависимость функции у и аргумента х задана посредством параметра t ( параметрически) 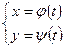 , то
, то  .
.
Пример: 
 .
.
Правило Лопиталя раскрытия неопределенностей.
Пусть функции f(x) и  дифференцируемы в окрестности точки а, причем производная
дифференцируемы в окрестности точки а, причем производная 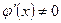 .
.
Если обе функции бесконечно малые или бесконечно большие при 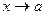 , т.е. если частное
, т.е. если частное 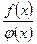 в точке а представляет неопределенность вида
в точке а представляет неопределенность вида  или
или  , то
, то  , при условии, что предел отношения производных существует (конечный или бесконечный).
, при условии, что предел отношения производных существует (конечный или бесконечный).
Правило применимо и для случая, когда 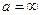 . Раскрытие неопределенностей вида
. Раскрытие неопределенностей вида  ,
, 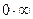 ,
, 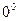 ,
, 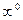 ,
, 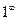 при помощи алгебраических преобразований и логарифмирования сводится к раскрытию неопределенностей вида
при помощи алгебраических преобразований и логарифмирования сводится к раскрытию неопределенностей вида  и
и  .
.
Примеры:
1. 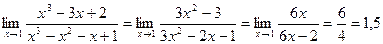 .
.
Здесь мы имеем неопределенность вида  и правило Лопиталя применяли дважды.
и правило Лопиталя применяли дважды.
2.  .
.
Здесь мы имеем неопределенность вида  и правило Лопиталя применяли трижды.
и правило Лопиталя применяли трижды.
3.  .
.
4.  .
.
Полагаем у = хх и логарифмируем обе части этого равенства:  . Найдем
. Найдем  . Из примера 3 видно:
. Из примера 3 видно: 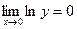 . Отсюда
. Отсюда 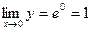 .
.
5.  .
.
Положим 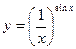 и прологарифмируем обе части полученного равенства:
и прологарифмируем обе части полученного равенства:  .
.
Найдем предел  :
: 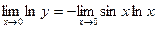 .
.
Полученную неопределенность вида 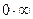 преобразуем к неопределенности вида
преобразуем к неопределенности вида  , а затем применим правило Лопиталя:
, а затем применим правило Лопиталя:  .
.
Отсюда получаем 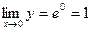 .
.
6. 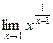 .
.
Положим 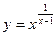 . При помощи логарифмирования получаем:
. При помощи логарифмирования получаем: 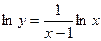 .
.
 , отсюда
, отсюда 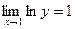 , т.е.
, т.е. 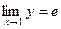 , т.е.
, т.е. 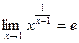 .
.
Замечание: правило Лопиталя применимо тогда, когда существует предел отношения производных. Если предел отношения функций существует, а предел отношения производных не существует, надо раскрывать неопределенности другим способом, например,  , а отношение производных
, а отношение производных 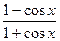 при
при  предела не имеет. Кроме того, производная знаменателя
предела не имеет. Кроме того, производная знаменателя 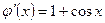 обращается в нуль в точках
обращается в нуль в точках 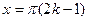 , что является нарушением условия правила Лопиталя.
, что является нарушением условия правила Лопиталя.
Производную 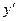 от у = f(x) будем называть производной первого порядка; производную от первой производной называют второй производной (или производной второго порядка) от функции у = f(x) и обозначают
от у = f(x) будем называть производной первого порядка; производную от первой производной называют второй производной (или производной второго порядка) от функции у = f(x) и обозначают  или
или 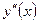 ; производную от производной второго порядка называют третьей производной и обозначают
; производную от производной второго порядка называют третьей производной и обозначают 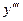 или
или 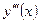 и т.д.
и т.д.
Производная от производной (n – 1)-го порядка называется производной n-го порядка от функции у = f(x) и обозначается  или
или  .
.
Пример: найти производные указанного порядка от данных функций:
1.  ;
; 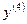 = ?
= ?
2. 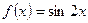 ;
; 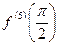 = ?
= ?
Решение:
1. найдем первую производную: 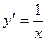 , теперь найдем вторую производную:
, теперь найдем вторую производную:  .
.
Продифференцируем еще два раза и получим производную четвертого порядка:  ;
;  .
.
2. Аналогично предыдущему примеру ищем сначала производную первого порядка, а затем более высоких:
 ,
,  ;
; 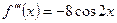 ;
;  ;
; 
При 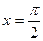 найдем
найдем 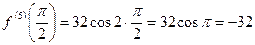 .
.
Пример: Показать, что функция у = cos2х удовлетворяет дифференциальному уравнению 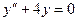 .
.
Решение: определяем 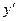 и
и  :
:  ;
; 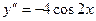 .
.
Подставив 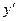 и
и  в данное уравнение, получим тождество:
в данное уравнение, получим тождество:  , т.е. 0 = 0.
, т.е. 0 = 0.
Если функция у = f(x) дифференцируема в интервале (a,b) и имеет положительную (отрицательную) производную 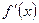 , то функция f(x) возрастает (убывает) в этом интервале.
, то функция f(x) возрастает (убывает) в этом интервале.
Замечание: производная в отдельных точках интервала может равняться нулю.
Пример: Найти промежутки возрастания и убывания следующих функций:
1. 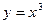 ;
;
2. 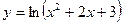 ;
;
3.  ;
;
4. 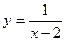 .
.
Решение:
1. Функция определена в интервале 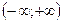 . Найдем производную
. Найдем производную 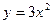 .
.
Производная 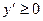 (обращается в нуль только в одной точке х = 0), следовательно, функция возрастает в интервале
(обращается в нуль только в одной точке х = 0), следовательно, функция возрастает в интервале 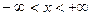 (см. рисунок).
(см. рисунок).
 2. Функция определена в интервале
2. Функция определена в интервале 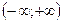 . Находим производную
. Находим производную 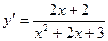 . Знаменатель дроби
. Знаменатель дроби 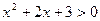 при любых значениях х (т.к. корни трехчлена комплексные), следовательно, знак производной совпадает со знаком числителя:
при любых значениях х (т.к. корни трехчлена комплексные), следовательно, знак производной совпадает со знаком числителя:  , если
, если 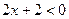 , т.е.
, т.е. 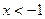
 , если
, если 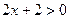 , т.е.
, т.е.  .
.
Функция убывает в интервале 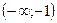 и возрастает в интервале
и возрастает в интервале 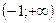 . В точке х = -1 убывание сменяется возрастанием.
. В точке х = -1 убывание сменяется возрастанием.
3. Данная функция определена при 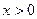 . Найдем производную:
. Найдем производную:  .
.
Функция возрастает, если 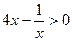 , т.е.
, т.е. 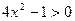
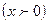 , или
, или  , т.е.
, т.е. 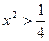 , или
, или 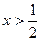 .
.
Функция убывает, если  , т.е.
, т.е.  , или
, или 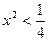 , т.е.
, т.е.  .
.
Итак, в интервале  функция убывает, в интервале
функция убывает, в интервале 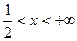 возрастает. В точке
возрастает. В точке  убывание сменяется возрастанием.
убывание сменяется возрастанием.
4. Точка х = 2 есть точка разрыва второго рода:  , при
, при 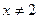 .
.
Следовательно, функция убывает в интервалах  и
и 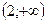 .
.
Функция у = f(x) имеет в точке х0 максимум (минимум) f(x0), если в некоторой окрестности этой точки (при 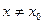 ) выполняется неравенство f(x) < f(x0) (f(x) > f(x0)).
) выполняется неравенство f(x) < f(x0) (f(x) > f(x0)).
Максимум или минимум функции называется экстремумом функции. Точка, в которой функция имеет минимум или максимум, называется точкой экстремума функции.
Если функция f(x) в точке х0 имеет экстремум, то производная в этой точке равна нулю, либо не существует (необходимое условие существования экстремума).
Точки возможного экстремума функции f(x) называются критическими точками для f(x).
Замечание: если х0 – критическая точка, то касательная в соответствующей точке М0 (х0,у0) графика функции параллельна оси Ох ( 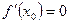 ) или Оу (
) или Оу ( 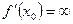 ), либо вовсе не существует, также заметим, что критические точки лежат внутри области определения функции.
), либо вовсе не существует, также заметим, что критические точки лежат внутри области определения функции.
Сформулируем достаточные признаки существования экстремума:
1. Если при переходе (слева направо) через критическую точку х0 производная 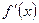 меняет знак с плюса на минус, то в точке х0 функция f(x) имеет максимум; если с минуса на плюс, то минимум; если знака не меняет, то экстремума нет.
меняет знак с плюса на минус, то в точке х0 функция f(x) имеет максимум; если с минуса на плюс, то минимум; если знака не меняет, то экстремума нет.
Для определения экстремума функции удобно использовать следующую схему:
- определить критические точки, т.е. найти действительные корни уравнения 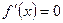 , а затем найти и те точки из области определения функции, в которых производная не существует;
, а затем найти и те точки из области определения функции, в которых производная не существует;
- исследовать на экстремум каждую критическую точку по первому достаточному признаку существования экстремума.
2. Пусть 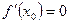 и в окрестности точки х0 существует конечная первая производная, а в самой точке х0 – вторая производная
и в окрестности точки х0 существует конечная первая производная, а в самой точке х0 – вторая производная  , тогда:
, тогда:
- если  , то в точке х0 имеется минимум;
, то в точке х0 имеется минимум;
- если  , то имеем максимум;
, то имеем максимум;
- если  , то этот признак ничего не дает и для решения вопроса надо применять первый достаточный признак.
, то этот признак ничего не дает и для решения вопроса надо применять первый достаточный признак.
Пример: Исследовать на максимум и минимум функцию 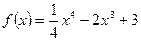 .
.
Решение: Функция определена и непрерывна на всей числовой оси. Найдем производную, приравняем ее к нулю и определим действительные корни:  ;
; 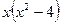 =0.
=0.
Следовательно, х1 = 0, х2 = 2, х3 = -2 – критические точки. Теперь исследуем знак производной в окрестности каждой из этих точек:
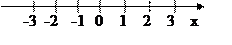 Так как левее точки х = -2 критических точек нет, то можно взять любое значение х и слева от точки –2, например, х = -3. Производная в этой точке имеет знак минус
Так как левее точки х = -2 критических точек нет, то можно взять любое значение х и слева от точки –2, например, х = -3. Производная в этой точке имеет знак минус
 , справа, при х = -1, – знак плюс
, справа, при х = -1, – знак плюс 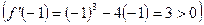 , следовательно, в точке х = -2 будет минимум (min).
, следовательно, в точке х = -2 будет минимум (min).
Слева от точки х = 0, как уже установлено, производная имеет знак плюс, справа можно брать любое значение х между 0 и 2, например, при х = 1 знак производной будет минус, т.е. в точке 0 мы имеем максимум (max).
Слева от точки 2, как уже известно, знак производной минус, т.е. нужно взять любое значение х правее точки 3, т.к. справа больше нет других критических точек, например, х = 3.  , следовательно, в точке х = 2 имеем минимум.
, следовательно, в точке х = 2 имеем минимум.
Найдем точки пересечения графика функции с осью Ох, пусть у = 0, тогда  ,
,  . Решая это уравнение, получаем:
. Решая это уравнение, получаем:  ;
;  ;
; 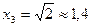 ;
; 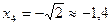 . С осью Оу имеем одну точку пересечения у = 3 (при х = 0).
. С осью Оу имеем одну точку пересечения у = 3 (при х = 0).
Воспользовавшись результатами, записанными в следующей таблице:
| х | 
| -2 | (-2;0) | 0 | (0;2) | 2 | 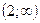
|
| у | -1 | 3 | -1 | ||||
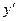
| <0 | 0 | >0 | 0 | <0 | 0 | >0 |
| вывод | 
| min | 
| max | 
| min | 
|

 Примечание: стрелки ( ) обозначают убывание (возрастание) функции на некотором данном интервале.
Примечание: стрелки ( ) обозначают убывание (возрастание) функции на некотором данном интервале.
А так же найденными точками пересечения кривой с осью Ох и Оу, построим график функции:
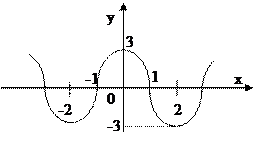 Примечание: ординаты точек экстремума находятся при помощи подстановки их абсцисс в уравнение кривой, например:
Примечание: ординаты точек экстремума находятся при помощи подстановки их абсцисс в уравнение кривой, например:
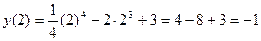
3.12. График дифференцируемой функции у = f(x) называется выпуклым (вогнутым) на интервале (a,b), если дуга кривой у = f(x) (a < x < b) расположена ниже (соответственно выше) касательной, проведенной в любой точке этой дуги.

Если на (a,b) существует  , то достаточным условием выпуклости (вогнутости) является выполнение неравенства
, то достаточным условием выпуклости (вогнутости) является выполнение неравенства 
 при a < x < b.
при a < x < b.
Точки, в которых выпуклость изменяется на вогнутость или наоборот, называется точками перегиба.
Если М(х0,у0) – точка перегиба графика функции у = f(x), то вторая производная 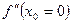 или не существует.
или не существует.
Пример: Найти точки перегиба следующих функций:
1. 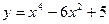 ;
;
2. 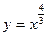 .
.
Решение:
1. Найдем вторую производную:  ;
;  .
.
Решим уравнение  ;
; 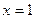 .
.
Исследуем знак второй производной в окрестности точек 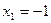 , х2 = 1.
, х2 = 1.
При 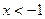 ,
,  и при
и при  ,
,  . (Знаки производных определяются аналогично примеру из п. 3.11. данного раздела).
. (Знаки производных определяются аналогично примеру из п. 3.11. данного раздела).
При 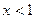 ,
,  и при
и при  ,
,  . Следовательно, точки перегиба: М1(-1;0) и М2(1;0). Результаты исследования удобнее сразу заносить в таблицу:
. Следовательно, точки перегиба: М1(-1;0) и М2(1;0). Результаты исследования удобнее сразу заносить в таблицу:
| х | 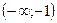
| -1 | (-1;1) | 1 | 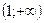
|

| >0 | 0 | <0 | 0 | >0 |
| вывод | вогнутость | перегиб | выпуклость | перегиб | вогнутость |
 т.е. в интервале
т.е. в интервале 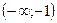 , где
, где  , кривая вогнута; в интервале (-1;1), где
, кривая вогнута; в интервале (-1;1), где  , кривая выпукла; в интервале
, кривая выпукла; в интервале 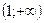 , где
, где  , вогнута.
, вогнута.
2.  ;
;  .
.
Производная  нигде не обращается в нуль. Приравнивая к нулю ее знаменатель, получаем, что в точке х = 0 вторая производная не существует. Исследуем знак второй производной в окрестности этой точки:
нигде не обращается в нуль. Приравнивая к нулю ее знаменатель, получаем, что в точке х = 0 вторая производная не существует. Исследуем знак второй производной в окрестности этой точки: 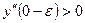 ,
,  , где
, где 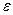 - некоторое положительное число.
- некоторое положительное число.
Точек перегиба нет. На интервале 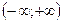 вогнутость кривой направлена вверх.
вогнутость кривой направлена вверх.
Пусть функция у = f(x) определена при всех х > х0, (х < x0). Если существуют числа k и b такие, что функция  при
при  (
( 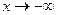 ), то прямую линию
), то прямую линию  называют асимптотой графика функции у = f(x) при
называют асимптотой графика функции у = f(x) при  (
( 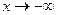 ).
).
При этом если 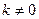 , то асимптоту называют наклонной, если k = 0 (тогда y = b), то горизонтальной.
, то асимптоту называют наклонной, если k = 0 (тогда y = b), то горизонтальной.
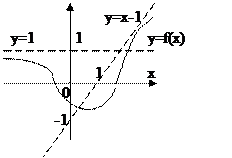 Условие f(x) – kx – b = 0 означает
Условие f(x) – kx – b = 0 означает  , и, следовательно, функция f(x) при
, и, следовательно, функция f(x) при  (
( 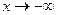 ) неограниченно
) неограниченно
приближается к прямой y = kx + b (ведет себя почти как линейная функция).
Например, на рисунке изображен график функции, имеющий наклонную асимптоту у = х – 1 при  (правая наклонная асимптота) и горизонтальную асимптоту у = 1, при
(правая наклонная асимптота) и горизонтальную асимптоту у = 1, при 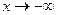 (левая горизонтальная асимптота).
(левая горизонтальная асимптота).
Если существуют пределы 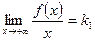 и
и  , то прямая
, то прямая 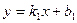 является наклонной асимптотой (при k1 = 0 – горизонтальной) графика функции y = f(x).
является наклонной асимптотой (при k1 = 0 – горизонтальной) графика функции y = f(x).
Если существуют пределы 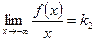 и
и  ,то прямая
,то прямая  является левой наклонной асимптотой (при k2 = 0 – горизонтальной) асимптотой графика функции y = f(x).
является левой наклонной асимптотой (при k2 = 0 – горизонтальной) асимптотой графика функции y = f(x).
Пусть функция у = f(x) определена в некоторой окрестности точки x = x0. Если  или
или  , то прямая х = х0 является вертикальной асимптотой графика функции у = f(x).
, то прямая х = х0 является вертикальной асимптотой графика функции у = f(x).
Пример: Найти асимптоты кривой 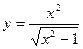 .
.
Решение: Приравнивая знаменатель к нулю, получаем две вертикальные асимптоты: х = -1, х = 1.
|
 получаем:
получаем: 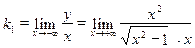
 , следовательно, правой асимптотой является прямая у = х, аналогично при
, следовательно, правой асимптотой является прямая у = х, аналогично при 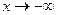 имеем:
имеем:  ,
, 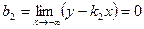 .
.
Таким образом, левая асимптота у = -х.
 Замечание: исследование на асимптоты данной кривой упрощается, если учесть симметрию этой кривой.
Замечание: исследование на асимптоты данной кривой упрощается, если учесть симметрию этой кривой.
3.13. Схема исследования функции и построения ее графика выглядит следующим образом:
1. область определения функции;
2. исследование на симметричность (четность, нечетность) и периодичность;
3. точки пересечения с осями координат (если это не вызывает особых осложнений);
4. точки экстремума и экстремальные значения;
5. точки разрыва;
6. интервалы возрастания и убывания;
7. точки перегиба, интервалы выпуклости и вогнутости;
8. асимптоты;
9. предельные значения функции при х, стремящемся к граничным точкам области определения.
В ходе построения графика по мере необходимости можно получить дополнительно ряд значений функции при некоторых частных значениях аргумента х, т.е. еще ряд точек графика. Строго придерживаться этой схемы не всегда обязательно. Часто бывает удобно изменить ее порядок.
Наименьшее (наибольшее) значение непрерывной функции f(x) на данном отрезке [a,b] достигается или в критических точках функции, или на концах отрезка [a,b].
Пример: Найти наибольшее и наименьшее значение функции  на отрезке
на отрезке  .
.
Решение: Так как 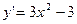 , то критическими точками функции являются
, то критическими точками функции являются 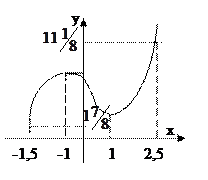 х1=-1 и х2 = 1.
х1=-1 и х2 = 1.
Сравнивая значения функции в этих точках и значения функции на концах отрезка 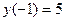 ;
;  ;
;  ;
;  , заключаем, что наименьшее значение функции m = 1 достигается в точке х = 1 (в точке минимума), а наибольшее
, заключаем, что наименьшее значение функции m = 1 достигается в точке х = 1 (в точке минимума), а наибольшее 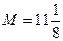 достигается в точке х = 2,5 (на правом конце отрезка).
достигается в точке х = 2,5 (на правом конце отрезка).
Примечание: студенты часто путают минимум (максимум) функции и наименьшее (наибольшее) значение функции. Это не одно и то же! Они очень часто не совпадают.
Пример: Проволокой длиной 20 м требуется огородить клумбу, которая должна иметь форму кругового сектора. Какой следует взять радиус круга, чтобы площадь клумбы была наибольшей?
 Решение: Обозначим радиус круга через х, а длину дуги сектора через у. Площадь кругового сектора
Решение: Обозначим радиус круга через х, а длину дуги сектора через у. Площадь кругового сектора  . Так как нам нужно сделать клумбу наибольшего размера, то исследуем функцию S на максимум.
. Так как нам нужно сделать клумбу наибольшего размера, то исследуем функцию S на максимум.
Сразу же заметим, что S зависит от 2-х переменных и у, поэтому выразим у через х (можно и наоборот). По условию задачи длина проволоки равна 20 метров, т.е. 2х + у = 20 (уравнение связи), поэтому у = 2(10 – х).
Следовательно: 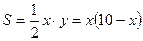 ,
,
 , 10 – 2х = 0, х = 5.
, 10 – 2х = 0, х = 5.
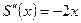 ,
,  (max) (
(max) (  - функция постоянная, равная –2 в любой точке, следовательно, и
- функция постоянная, равная –2 в любой точке, следовательно, и 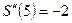 ).
).
Таким образом, радиус круга надо взять равным 5 м.
Переменная z называется однозначной функцией от переменных х и у, если каждой паре значений х и у из области их изменения соответствует одно значение z.
Переменные х и у называются независимыми переменными или аргументами, z-зависимой переменной.
Функциональная зависимость обозначается так: 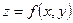 .
.
Областью определения функции 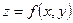 называется совокупность точек (х;у) плоскости хОу, в которой заданная функция определена, т.е. принимает действительные значения. Геометрическим изображением функции
называется совокупность точек (х;у) плоскости хОу, в которой заданная функция определена, т.е. принимает действительные значения. Геометрическим изображением функции 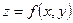 является некоторая поверхность в пространстве. Частное (числовое) значение функции
является некоторая поверхность в пространстве. Частное (числовое) значение функции  при х = х0, у = у0 обозначается так:
при х = х0, у = у0 обозначается так:  .
.
Аналогично определяются функции от большего числа переменных:  .
.
Пример: Найти область определения функции 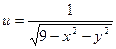 и вычислить ее частное значение при х = 2, у = 1.
и вычислить ее частное значение при х = 2, у = 1.
Решение: Функция существует лишь для тех пар значений х и у, которые удовлетворяют неравенству 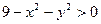 , откуда
, откуда  , т.е. область определения функции есть круг, с центром в начале координат и радиусом r = 3 (не включая границ круга, т.е. окружность
, т.е. область определения функции есть круг, с центром в начале координат и радиусом r = 3 (не включая границ круга, т.е. окружность 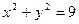 ). Найдем частное значение функции:
). Найдем частное значение функции: 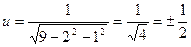 .
.
Последовательность точек 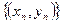 сходится к точке при (х0,у0), если
сходится к точке при (х0,у0), если 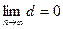 , где
, где 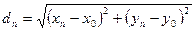 . Пусть функция f(x,y) определена внутри некоторого круга К с центром в точке (х0,у0), за исключением, быть может, самой точки (х0,у0).
. Пусть функция f(x,y) определена внутри некоторого круга К с центром в точке (х0,у0), за исключением, быть может, самой точки (х0,у0).
Число А называется пределом функции z = f(x,y) в точке М0(х0,у0), если для любой последовательности точек 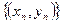 области определения функций, отличных от (х0,у0) и сходящихся к (х0,у0), последовательность значений функций
области определения функций, отличных от (х0,у0) и сходящихся к (х0,у0), последовательность значений функций 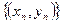 сходится к А. Обозначение
сходится к А. Обозначение  .
.
Если 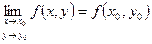 , то функция f(x,y) называется непрерывной в точке (х0,у0).
, то функция f(x,y) называется непрерывной в точке (х0,у0).
Замечание: это определение в другой записи выглядит следующим образом:  или
или  .
.
Функция непрерывна в каждой точке своей области, называется непрерывной в этой области.
Если существует предел  , то он называется частной производной функции z по х в точке (х0,у0) и обозначается символами
, то он называется частной производной функции z по х в точке (х0,у0) и обозначается символами  или
или  .
.
Аналогично определяется частная производная по y.
Примечание: на практике для нахождения частных производных пользуются теми же правилами дифференцирования, что и для функции 2-х переменных, помня, что  ,
,  .
.
Пример: Найти частные производные функции  .
.
Решение: Рассматривая у как постоянную величину, дифференцируем функцию только по переменной х: 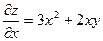 . Аналогично, рассматривая х как постоянную величину, имеем:
. Аналогично, рассматривая х как постоянную величину, имеем:  .
.
Замечание: Частное значение функций нескольких переменных в некоторой точке вычисляется аналогично функции 2-х переменных путем подстановки координат точки в полученную частную производную.
Полным приращением функции z = f(x,y) называется разность  .
.
Линейная (главная) часть приращения функции z = f(x,y) относительно приращения аргументов 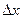 и
и 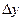 называется ее полным дифференциалом и обозначается dz или df(x,y).
называется ее полным дифференциалом и обозначается dz или df(x,y).
Функция f(x,y) называется дифференцируемой в точке (x,y), если она имеет полный дифференциал в этой точке.
Полный дифференциал функции z = f(x,y) обычно находят по формуле
 ,
,
где  ,
,  .
.
При достаточно малых 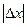 и
и 
 или
или  .
.
Пример: Найти полное приращение и полный дифференциал функции 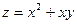 при х = 2; у = 1;
при х = 2; у = 1; 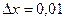 ;
;  .
.
Решение: Воспользуемся формулой для полного приращения и определением полного дифференциала функции z = f(x,y):  , откуда
, откуда 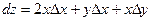 . Подставляя данные в условии значения, получаем
. Подставляя данные в условии значения, получаем 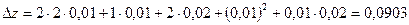 .
.
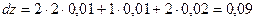 .
.
Пример: Найти полный дифференциал функции 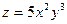 .
.
Решение: Сначала найдем частные производные: 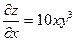 ,
, 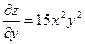 .
.
По формуле полного дифференциала получаем:  .
.
Линией уровня функции z = f(x,y) называется такая линия f(x,y) = c на плоскости хОу, в точках которой функция понимает одно и то же значение
z = c (обычно проставляемое на чертеже в виде отметки).
Поверхностью уровня функции 3-х аргументов  называется такая поверхность
называется такая поверхность 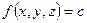 , в точках котрой функция принимает постоянное значение u = c.
, в точках котрой функция принимает постоянное значение u = c.
Пример: Построить линии уровня функции  .
.
Решение: Уравнение линий уровня имеет вид  или
или 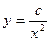 . Полагая
. Полагая  получим семейство линий уровня.
получим семейство линий уровня.
 Производной функции z = f(x,y) в точке Р в данном направлении
Производной функции z = f(x,y) в точке Р в данном направлении 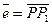 называется
называется 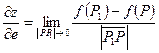 , где f(P) и f(P1) – значения функции в точках Р и Р1 соответственно.
, где f(P) и f(P1) – значения функции в точках Р и Р1 соответственно.
Другими словами: под производной  функции в данном направлении
функции в данном направлении 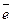 понимается предел отношения приращения функции в этом направлении к величине перемещения, при условии, что последняя стремится к нулю.
понимается предел отношения приращения функции в этом направлении к величине перемещения, при условии, что последняя стремится к нулю.
 Если функция z дифференцируема, то справедлива формула
Если функция z дифференцируема, то справедлива формула 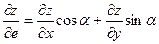 , где
, где  - угол, образованный вектором
- угол, образованный вектором 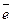 с осью Ох.
с осью Ох.
Производная  дает скорость изменения функции в направлении е.
дает скорость изменения функции в направлении е.
Примечание: для функции 3-х аргументов, аналогично:  , где
, где  ,
,  ,
, 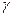 - углы между направлением
- углы между направлением 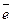 и соответствующими координатными осями.
и соответствующими координатными осями.
Пример: Найти производную функции 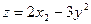 в точке Р (1;0) в направлении, составляющем с осью Ох угол, равный 1200.
в точке Р (1;0) в направлении, составляющем с осью Ох угол, равный 1200.
Решение: Найдем частные производные данной функции и их значения в точке Р:  ;
;  ;
;  ;
;  . Здесь
. Здесь 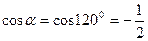 ,
, 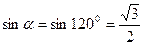 . Следовательно:
. Следовательно:  .
.
Знак минус показывает, что функция в данной точке и в данном направлении убывает.
Градиентом функции z = f(x,y) в точке Р (х,у) называется вектор, проекции которого на координатные оси являются соответствующие частные производные данной функции:
 .
.
Градиент функции в каждой точке направлен по нормали к соответствующей линии уровня функции. Направление градиента функции в данной точке есть направление наибольшей скорости возрастания функции в этой точке.
Аналогично определяется градиент функции 3-х аргументов.
Производную по направлению  на практике удобно вычислять, используя скалярное произведение
на практике удобно вычислять, используя скалярное произведение 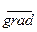 U и единичного вектора
U и единичного вектора  направления
направления 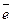 :
:
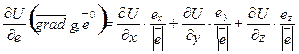 .
.
Пример: Найти поверхности уровня скалярного поля  , вычислить производную поля в точке
, вычислить производную поля в точке  по направлению вектора
по направлению вектора  , где В(0;-4;3).
, где В(0;-4;3).
Решение: Поверхностями уровня данного поля являются концентрические сферы с центром в начале координат: 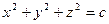 .
.
Градиент U вычислим через частные производные: 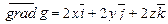 .
.
Найдем единичный вектор  :
: 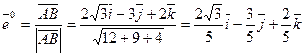 .
.
Производная скалярного поля U по направлению вектора  в точке А:
в точке А:
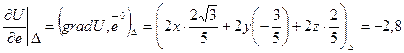 , т.к.
, т.к. 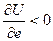 , то данное скалярное поле убывает в направлении вектора
, то данное скалярное поле убывает в направлении вектора 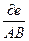 .
.
Говорят, что в данной области  (на множестве
(на множестве  ) определено скалярное поле, если для каждой точки
) определено скалярное поле, если для каждой точки  задан некоторый скаляр: u = f(M), то есть числовая функция точки.
задан некоторый скаляр: u = f(M), то есть числовая функция точки.
Примеры скалярных полей: температурное поле (распределение температуры в нагретом теле); распределение концентрации вещества в растворе и т.п.
Если область  расположена на плоскости хОу, то любая ее точка М определяется двумя координатами (х,у), и плоское скалярное поле (т.е. f(x,y) – функция двух переменных) может быть записано в виде:
расположена на плоскости хОу, то любая ее точка М определяется двумя координатами (х,у), и плоское скалярное поле (т.е. f(x,y) – функция двух переменных) может быть записано в виде:

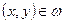 ,
,
т.е. скалярное поле – физическая трактовка функции нескольких переменных.
Векторным полем, определенным в данной области  , называется векторная функция точки
, называется векторная функция точки  :
:
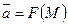 ,
,
т.е. для каждой точки  задан некоторый вектор.
задан некоторый вектор.
Примеры векторных полей: поле скоростей в данный момент времени точек потока жидкости; силовое поле, создаваемое некоторым притягивающим центром, и т.п.
Для функции 2-х аргументов, при переходе к координатам вектора  будет:
будет:
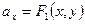 ,
, 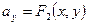 ,
,
т.е. задание векторного поля равносильно заданию 2-х скалярных полей.
Примечание: как видите, удобство «векторного языка» позволяет в одной векторной формуле записывать несколько скалярных соотношений.
Примечание: скалярное поле порождает векторное поле градиентов
 .
.
Пример: Найти и построить градиент функции  в точке Р(1;1).
в точке Р(1;1).
Решение: Вычислим частные производные и их значения в точке Р: 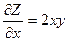 ;
;
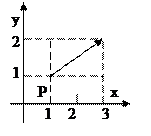
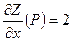 ;
;  ;
; 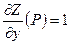 .
.
Следовательно, 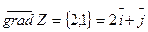 .
.
Частными производными второго порядка функции z = f(x,y) называются частные производные от ее частных производных первого порядка.
Обозначения:
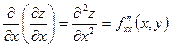 ,
, 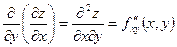 и т.д.
и т.д.
Аналогично определяются частные производные более высоких порядков.
Пример: Найти частные производные второго порядка от функции  .
.
Решение: Сначала найдем частные производные первого порядка: 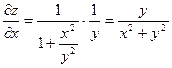 ;
;  .
.
Теперь дифференцируем вторично:  ,
,  ,
, 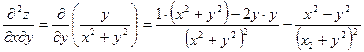 ,
,
 .
.
Примечание: обратите внимание на так называемые «смешанные частные производные»: 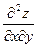 и
и  . Они оказались равными. Запомните это факт исключительной важности для практических приложений.
. Они оказались равными. Запомните это факт исключительной важности для практических приложений.
Дифференциалом второго порядка функции z = f(x,y) называется дифференциал от дифференциала первого порядка этой функции:
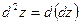 .
.
На практике дифференциал второго порядка вычисляется по формуле:
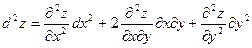 ,
,
если f(x,y) имеет непрерывные частные производные второго порядка.
Пример: Найти полные дифференциалы 1-го и 2-го порядка функции 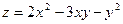 .
.
Решение: Имеем: 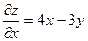 ,
,  . Поэтому
. Поэтому  .
.
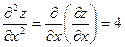 ;
; 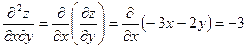 ;
;
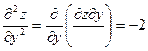 , т.е.
, т.е. 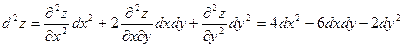 .
.
Можно применить и другой способ нахождения дифференциала.
Дифференцированием находим:  .
.
Дифференцируем еще раз, помня, что dx и dy не зависят от х и у: 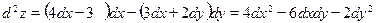 .
.
Функция f(x,y) имеет максимум (минимум) f(a,b) в точке Р(a,b), если для всех отличных от Р точек  в достаточно малой окрестности точки Р выполнено неравенство f(a,b) > f(x,y) (или соответственно f(a,b) < f(x,y))).
в достаточно малой окрестности точки Р выполнено неравенство f(a,b) > f(x,y) (или соответственно f(a,b) < f(x,y))).
Максимум или минимум функции называется ее экстремумом.
Необходимые условия экстремума: точки, в которых дифференцируемая функция f(x,y) может достигать экстремума (стационарные точки), находится путем решения системы уравнений:
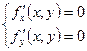 .
.
Замечание: эта система эквивалентна одному уравнению df(x,y) = 0. В общем случае в точке экстремума P(a,b) функция f(x,y) или df(a,b) = 0 или df(a,b) не существует.
Достаточные условия экстремума:
1. Если 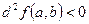 при
при  , то f(a,b) – есть максимум функции f (x,y).
, то f(a,b) – есть максимум функции f (x,y).
2. Если  при
при  , то f(a,b) – есть минимум функции f (x,y).
, то f(a,b) – есть минимум функции f (x,y).
3. Если 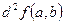 меняет знак, то f(a,b) не является экстремумом.
меняет знак, то f(a,b) не является экстремумом.
Приведенные условия на практике проще заменить следующими эквивалентами:
Пусть 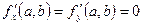 и
и 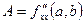 ,
,  ,
,  . Составим дискриминант:
. Составим дискриминант:
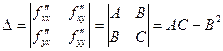 , тогда:
, тогда:
1. Если 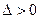 , то в точке Р(a,b) функция имеет экстремум, а именно, максимум при А < 0 (или С < 0), и минимум, если А > 0 (С > 0);
, то в точке Р(a,b) функция имеет экстремум, а именно, максимум при А < 0 (или С < 0), и минимум, если А > 0 (С > 0);
2. Если 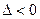 , то экстремума в точке Р(a;b) нет;
, то экстремума в точке Р(a;b) нет;
3. Если  , то вопрос о наличии экстремума в точке P(a;b) остается открытым, т.е. требуется дальнейшее исследование.
, то вопрос о наличии экстремума в точке P(a;b) остается открытым, т.е. требуется дальнейшее исследование.
Пример: Исследовать на экстремум функцию 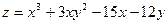 .
.
Решение: Найдем частные производные и составим систему уравнений (необходимое условие экстремума):  ;
; 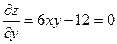 , или
, или 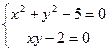 .
.
Решив систему уравнений, получим четыре стационарные точки: 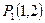 ,
,  ,
, 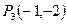 ,
, 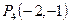 .
.
Найдем производные 2-го порядка: 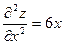 ,
, 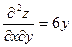 ,
,  и составим дискриминант
и составим дискриминант  для каждой стационарной точки.
для каждой стационарной точки.
Для  :
:  ,
, 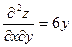 ,
,  ; дискриминант
; дискриминант  , значит в точке
, значит в точке 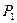 экстремума нет.
экстремума нет.
Для 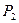 :
: 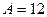 , В = 6, С = 12,
, В = 6, С = 12, 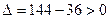 , А > 0, значит в точке
, А > 0, значит в точке 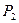 функция имеет минимум. Этот минимум равен значению функции при х = 2,
функция имеет минимум. Этот минимум равен значению функции при х = 2,
у = 1.
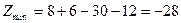
Для  : А = -6, В = -12, С = -6,
: А = -6, В = -12, С = -6,  - экстремума нет.
- экстремума нет.
Для  : А = -12, В = -6, С = -12,
: А = -12, В = -6, С = -12, 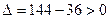 , А < 0 – максимум
, А < 0 – максимум

Условным экстремумом функции f(x,y) в простейшем случае называется максимум или минимум этой функции, достигнутый при условии, что ее аргументы связаны уравнением 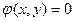 (уравнением связи).
(уравнением связи).
Для нахождения условного экстремума при наличии уравнения связи составляют функцию Лагранжа:
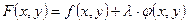 ,
,
где  - неопределенный постоянный множитель, и ищут экстремум этой вспомогательной функции.
- неопределенный постоянный множитель, и ищут экстремум этой вспомогательной функции.
Необходимые условия экстремума:

Функция f(x,y) имеет условный максимум, если 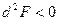 и условный минимум, если
и условный минимум, если 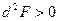 , где
, где  . В частности, если
. В частности, если 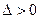 и
и
А < 0 (C < 0), то в этой точке имеется условный максимум, если А > 0 (C > 0), то условный минимум.
Пример: Найти экстремумы функции z = 6 – 4х – 3у при условии, что 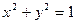 .
.
Решение:  . Имеем
. Имеем 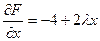 ,
, 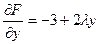 . Необходимые условия дают систему уравнений:
. Необходимые условия дают систему уравнений:
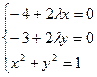 ,
,
решая которую, находим: 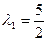 ,
, 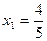 ,
, 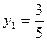 и
и 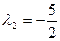 ,
,  ,
,  .
.
Так как 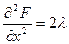 ,
,  ,
, 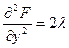 , то
, то 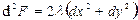 .
.
Если 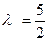 ,
,  и
и  , то
, то 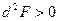 , т.е. в этой точке функция имеет условный минимум.
, т.е. в этой точке функция имеет условный минимум.
Если  ,
, 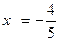 и
и 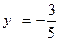 , то
, то 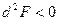 , и, следовательно, в этой точке функция имеет условный минимум.
, и, следовательно, в этой точке функция имеет условный минимум.
Таким образом,
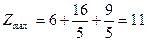
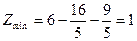
Функция, дифференцируемая в ограниченной замкнутой области, достигает своего наибольшего (наименьшего) значения или в стационарной точке, или в точке границы области.
Пример: Определить наибольшее и наименьшее значения функции 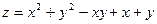 в области
в области 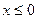 ,
,  ,
,  .
.
Решение: Указанная область есть треугольник, изображенный на рисунке.
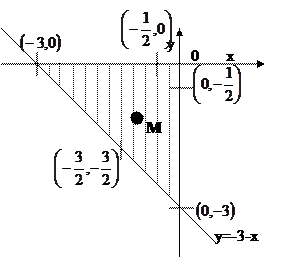
1.Найдем стационарные точки 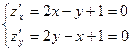 , отсюда х = -1, у = -1, получаем точку М(-1;-1). В точке М значение функции
, отсюда х = -1, у = -1, получаем точку М(-1;-1). В точке М значение функции 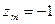 . Исследование на экстремум – не обязательно.
. Исследование на экстремум – не обязательно.
Примечание: Еще раз обратите внимание и запомните: максимум (или минимум) и наибольшее (или наименьшее) значение функции – это абсолютно разные понятия! Не путайте их.
2. Исследуем функцию на границах области.
При х = 0 имеем 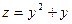 , и задача сводится к отысканию наибольшего и наименьшего значений этой функции одного аргумента на отрезке.
, и задача сводится к отысканию наибольшего и наименьшего значений этой функции одного аргумента на отрезке.
Проведя исследование, найдем, что 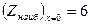 в точке (0;-3);
в точке (0;-3); 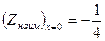 в точке
в точке 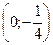 .
.
При у = 0 получаем 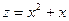 . Аналогично найдем, что
. Аналогично найдем, что 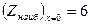 в точке (0;-3);
в точке (0;-3); 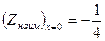 в точке
в точке 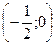 .
.
При х + у = -3 или у = -3 – х будет иметь  .
.
Аналогичным образом найдем, что  в точке
в точке  ;
;  совпадает с
совпадает с  и
и  . На прямой х + у = -3 можно было бы исследовать функцию на условный экстремум, не приводя к функции одного аргумента.
. На прямой х + у = -3 можно было бы исследовать функцию на условный экстремум, не приводя к функции одного аргумента.
3. Сопоставляя все полученные значения функции z, заключаем, что 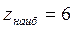 в точках (0;-3) и (-3;0);
в точках (0;-3) и (-3;0);  в стационарной точке М.
в стационарной точке М.
Тест №3
1. Касательная к графику функции  в точке с абсциссой х = 0 образует с осью Ох угол:
в точке с абсциссой х = 0 образует с осью Ох угол:
1) 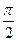 ; 2)
; 2)  ; 3) 60°; 4) p.
; 3) 60°; 4) p.
2. Наибольшее значение функции  на отрезке [-1,5; 2,5] достигается
на отрезке [-1,5; 2,5] достигается
1) в точке х = -1; 2) в точке х = 1; 3) х = 2,5; 4) х = -1,5.
3. Область определения функции 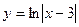 есть интервал:
есть интервал:
1) 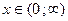 ;
;
2)  ;
;
3) 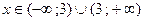 ;
;
4) правильный ответ отсутствует в предыдущих вариантах.
4.  в точке О(1, 1) для
в точке О(1, 1) для 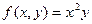 есть вектор:
есть вектор:
1)  ; 2)
; 2) 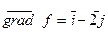 ;
;
3) 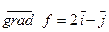 ; 4)
; 4)  .
.
Задания для контрольных и самостоятельных работ
I. Найти производные первого порядка данных функций, используя в п. в) логарифмическую производную, в задании д) найти производную обратной функции или функции заданной параметрами.
1. а) 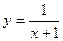 ; б) y = sin(3x + 1);
; б) y = sin(3x + 1);
в) 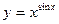 ; г) 2х – 3у + 1 = 0;
; г) 2х – 3у + 1 = 0;
д) найти 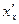 , если у = 3х + х2.
, если у = 3х + х2.
2. а)  ; б) у = (1 + 2х8);
; б) у = (1 + 2х8);
в) 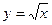 ; г)
; г) 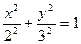 ;
;
д)  .
.
3. а) 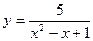 ; б) у = sin(x + sinx);
; б) у = sin(x + sinx);
в) 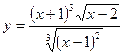 ; г)
; г) 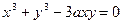 ;
;
д) найти  , если у = 2х2 + х.
, если у = 2х2 + х.
4. а) 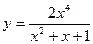 ; б) у = 5cos(2 – 3x);
; б) у = 5cos(2 – 3x);
в) 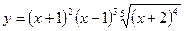 ; г)
; г) 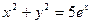 ;
;
д)  .
.
5. а) 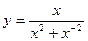 ; б) у = ctg(xsinx);
; б) у = ctg(xsinx);
в)  ; г)
; г) 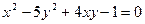 ;
;
д) найти  , если
, если 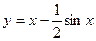 .
.
6. а) 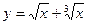 ; б)
; б)  ;
;
в) 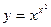 ; г)
; г) 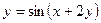 ;
;
д)  .
.
7. а) 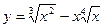 ; б) y = tg(3x + 1)3;
; б) y = tg(3x + 1)3;
в) 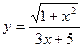 ; г) х2 + у2 = 1;
; г) х2 + у2 = 1;
д) найти  , если
, если  .
.
8. а) 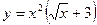 б)
б) 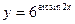 ;
;
в)  ; г) у2 = 4х;
; г) у2 = 4х;
д) 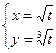 .
.
9. а) 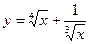 ; б)
; б) 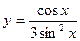 ;
;
в) у = хх; г) х = у + siny;
д) найти  , если
, если  .
.
10.а)  ; б)
; б) 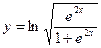 ;
;
в)  ; г)
; г)  ;
;
д) 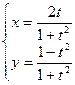 .
.
11.а) 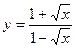 ; б)
; б) 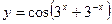 ;
;
в) 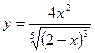 ; г)
; г)  ;
;
д) найти  , если
, если 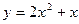 .
.
12.а) 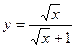 ; б)
; б)  ;
;
в) 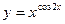 ; г)
; г)  ;
;
д) 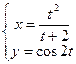 .
.
13.а)  ; б)
; б)  ;
;
в) 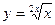 ; г)
; г)  ;
;
д) найти  , если
, если 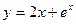 .
.
14.а)  ; б)
; б)  ;
;
в) 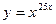 ; г)
; г)  ;
;
д)  .
.
15.а) 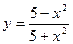 ; б)
; б) 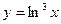 ;
;
в) 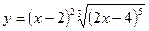 ; г)
; г) 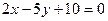 ;
;
д) найти  , если
, если 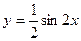 .
.
16.а)  ; б)
; б) 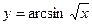 ;
;
в) 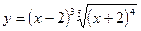 ; г)
; г) 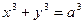 ;
;
д)  .
.
17.а)  ; б)
; б)  ;
;
в) 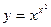 ; г)
; г)  ;
;
д) найти  , если
, если  .
.
18.а) 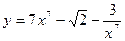 ; б)
; б) 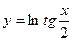 ;
;
в) 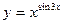 ; г)
; г)  ;
;
19.а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) найти  , если
, если  .
.
20.а) 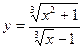 ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) 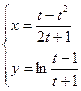 .
.
II. Составить уравнение касательной и нормали к кривой в указанной точке. Определить угол между касательной и осью Ох:
1. 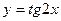 , ,  . .
| 11.  , , 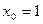 . .
|
2.  , , 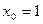
| 12. 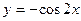 , ,  . .
|
3.  , , 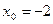 . .
| 13. 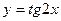 , , 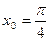 . .
|
4.  , ,  . .
| 14. 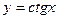 , , 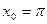 . .
|
5.  , , 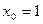 . .
| 15. 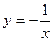 , , 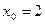 . .
|
6. 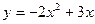 , , 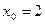 . .
| 16. 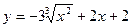 . .
|
7.  , ,  . .
| 17. 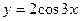 , ,  . .
|
8. 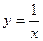 , , 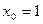 . .
| 18.  , , 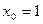 . .
|
9. 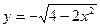 , , 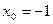 . .
| 19. 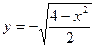 , , 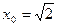 . .
|
10.  , , 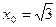 . .
| 20.  , , 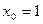 . .
|
III. Пользуясь правилом Лопиталя, вычислить указанный предел. Если это невозможно, то вычислить его каким-либо другим способом.
1. 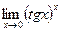 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5. 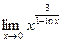 . 6.
. 6. 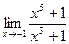 . 7.
. 7. 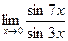 . 8.
. 8. 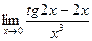 .
.
9.  . 10.
. 10.  . 11.
. 11.  . 12.
. 12. 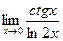 .
.
13.  . 14.
. 14.  . 15.
. 15.  . 16.
. 16.  .
.
17. 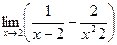 . 18.
. 18. 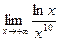 . 19.
. 19. 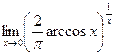 . 20.
. 20. 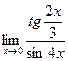 .
.
IV. Используя общую схему исследования и построения графика функции, построить следующие кривые:
1.  . 2.
. 2.  . 3.
. 3. 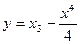 .
.
4.  . 5.
. 5.  . 6.
. 6.  .
.
7. 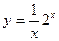 . 8.
. 8. 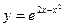 . 9.
. 9. 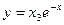 .
.
10. 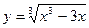 . 11.
. 11.  . 12.
. 12.  .
.
13.  . 14.
. 14.  . 15.
. 15. 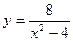 .
.
16. 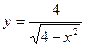 . 17.
. 17.  . 18.
. 18. 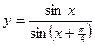 .
.
19. 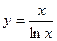 . 20.
. 20.  .
.
V. Решить задачу при помощи производных.
1. Бак цилиндрической формы должен вмещать 8 литров воды. Каковы должны быть его размеры, чтобы поверхность (без крышки) была наименьшей?
2. Окно имеет форму прямоугольника, завершенного полукругом. Периметр задан. Каковы должны быть размеры окна, чтобы оно пускало наибольшее количество света?
3. Резервуар, который должен иметь форму прямоугольного параллелепипеда (открытого сверху) с квадратным основанием нужно вылудить внутри оловом. Каковы должны быть размеры резервуара, чтобы на его лужение пошло наименьшее количество олова, если он должен вмещать 108 литров воды?
4. В треугольник с основанием b и высотой h вписать прямоугольник с наибольшей площадью.
5. Нужно построить прямоугольную площадку возле каменной стены, так чтобы с трех сторон она была огорожена проволочной сеткой, а четвертой примыкала к стене. Для этого имеется “а” погонных метров сетки. Каково должно быть соотношение сторон, чтобы площадка имела наибольшую площадь?
6. Требуется изготовить коническую воронку с образующей, равной 20 метров. Какова должна быть высота воронки, чтобы ее объем был наибольшим?
7. Найти высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R.
8. Найти соотношение между радиусом R и высотой H цилиндра, имеющего при данном объеме наименьшую полную поверхность.
9. Консервная банка данного объема имеет форму цилиндра. Каково должно быть соотношение ее размеров (высоты и диаметра), чтобы на изготовление пошло минимальное количество жести?
2. Какой сектор следует вырезать из круга радиуса R, чтобы из оставшейся части можно было свернуть воронку наибольшей вместимости?
3. Найти угол, под которым пересекаются параболы  и
и 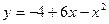 .
.
4. Закон движения точки по оси Ох есть  . Найти скорость движения точки, для моментов времени
. Найти скорость движения точки, для моментов времени 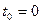 ,
, 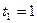 ,
, 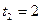 (х дается в сантиметрах, t – в секундах).
(х дается в сантиметрах, t – в секундах).
5. Показать, что гиперболы  и
и  пересекаются под прямым углом.
пересекаются под прямым углом.
6. Точка совершает колебательное движение по оси абсцисс по закону
x = 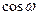 t. Найти момент времени, когда скорость равна нулю. Чему в это время равно х?
t. Найти момент времени, когда скорость равна нулю. Чему в это время равно х?
7. Количество электричества, протекшее через проводник, начиная с момента
t = 0 определяется формулой 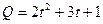 (к). Найти силу тока в конце десятой секунды.
(к). Найти силу тока в конце десятой секунды.
8. Прямоугольник вписан в эллипс с осями 2а и 2b. Каковы должны быть стороны прямоугольника, чтобы его площадь была наибольшей?
9. Из круглого бревна, диаметр которого равен d, требуется вырезать балку прямоугольного поперечного сечения. Каковы должны быть его ширина и высота, чтобы балка оказывала наибольшее сопротивление на изгиб?
Замечание: сопротивление балки на изгиб пропорционально произведению ширины х ее поперечного сечения на квадрат его высоты y: Q = kxy2, k = const.
10. Требуется изготовить из жести ведро цилиндрической формы без крышки данного объема V. Каковы должны быть высота ведра и радиус его дна, чтобы на его изготовление шло наименьшее количество жести?
11. Над центром круглой площадки радиуса R = 10 м нужно повесить фонарь. На какой высоте это нужно сделать, чтобы края площадки были максимально освещены?
Замечание: степень освещенности некоторой площадки пропорциональна косинусу угла падения лучей и обратно пропорциональна квадрату расстояния от источника света:  , k = const.
, k = const.
20. Требуется изготовить открытый цилиндрический бак данного объема V. Стоимость квадратного метра материала, идущего на изготовление дна бака, равна 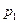 руб., а стенок -
руб., а стенок - 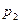 рублей. Каковы должны быть радиус дна и высота бака, чтобы затраты на материал для его изготовления были наименьшими?
рублей. Каковы должны быть радиус дна и высота бака, чтобы затраты на материал для его изготовления были наименьшими?
VI. Исследовать на экстремум данную функцию и найти ее наибольшее и наименьшее значение в указанной области:
1. 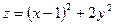 ;
;  ,
, 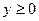 ;
;  .
.
2. 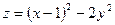 ;
;  ,
, 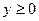 ;
;  .
.
3.  ;
;  ,
, 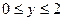 .
.
4.  ;
;  ,
,  .
.
5.  ;
;  ,
,  .
.
6.  ;
; 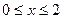 ,
, 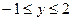 .
.
7. 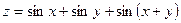 ;
; 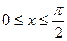 ,
, 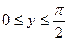 .
.
8.  ;
; 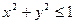 .
.
9. 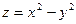 ;
; 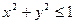 .
.
10.  ;
;  ,
, 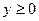 ;
; 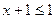 .
.
11.  ;
;  ;
; 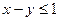 .
.
12. 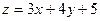 ;
; 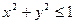 .
.
13. 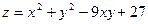 ;
;  ,
, 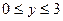 .
.
14. 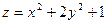 ;
;  ,
, 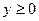 ;
; 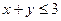 .
.
15.  ;
; 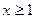 ,
, 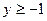 ;
; 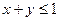 .
.
16. 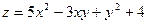 ;
;  ,
, 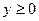 ;
; 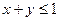 .
.
17. 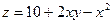 ;
; 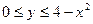 .
.
18.  ;
; 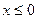 ,
,  ;
;  .
.
19. 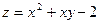 ;
;  .
.
20. 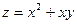 ;
;  ,
, 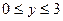 .
.
VII. Даны функция z = f(x,y), точка 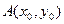 и вектор
и вектор 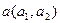 . Найти:
. Найти:
- gradZ в точке А;
- производную в точке А по направлению вектора А.
1. 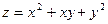 ; А (1,1), а (2,-1).
; А (1,1), а (2,-1).
2.  ; А (2,1), а (3,-4).
; А (2,1), а (3,-4).
3.  ; А (1,1), а (3,2).
; А (1,1), а (3,2).
4.  ; А (1,1), а (2,-1).
; А (1,1), а (2,-1).
5.  ; А (2,1), а (1,2).
; А (2,1), а (1,2).
6.  ; А (2,3), а (4,-3).
; А (2,3), а (4,-3).
7. 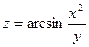 ; А (1,2), а (5,-12).
; А (1,2), а (5,-12).
8.  ; А (1,3), а (2,-1).
; А (1,3), а (2,-1).
9.  ; А (-1,2), а (4,-3).
; А (-1,2), а (4,-3).
10. 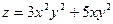 ; А (1,1), а (2,1).
; А (1,1), а (2,1).
11. 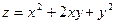 ; А (1,1), а (1,1).
; А (1,1), а (1,1).
12.  ; А (0,1), а (1,2).
; А (0,1), а (1,2).
13.  ; А (2,1), а (-1,1).
; А (2,1), а (-1,1).
14.  ; А (1,3), а (2,1).
; А (1,3), а (2,1).
15.  ; А (2,-1), а (-1,1).
; А (2,-1), а (-1,1).
16.  ; А (1,2), а (-2,1).
; А (1,2), а (-2,1).
17. 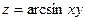 ; А (1,2), а (2,3).
; А (1,2), а (2,3).
18. 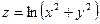 ; А (2,3), а (1,2).
; А (2,3), а (1,2).
19.  ; А (1,1), а (2,-1).
; А (1,1), а (2,-1).
20.  ; А (1,1), а (2,-1).
; А (1,1), а (2,-1).
Дата добавления: 2021-07-19; просмотров: 86; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
