Линейные дифференциальные уравнения первого
Министерство образования и науки Красноярского края
КГБПОУ «Боготольский техникум транспорта»
Занятие по теме:
ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ
Методические указания для специальности
23.02.06 Техническая эксплуатация подвижного состава железных дорог
среднего профессионального образования базовой подготовки
ОГЛАВЛЕНИЕ
Введение……………………………………………………………………
1.Дифференциальные уравнения первого порядка
с разделяющимися переменными…………………………..
2.Линейные дифференциальные уравнения первого
порядка……………………………………………………………….
Задачи для самостоятельного решения……………………………..
3.Дифференциальные уравнения второго порядка………….…
Задачи для самостоятельного решения……………………………..
Ответы…………………………………………………………………………
Литература……………………………………………………………………
ВВЕДЕНИЕ
Математическое описание самых разнообразных явлений, происходящих в природе, часто приводит к уравнениям, связывающим независимую переменную, искомую функцию (одной переменной) и производные этой функции. Такого рода уравнения называют обыкновенными дифференциальными уравнениями. (В дальнейшем будем называть их дифференциальными уравнениями). Если в дифференциальное уравнение входит только независимая переменная, функция и её первая производная, то уравнение называется дифференциальным уравнением первого порядка.
В общем виде его можно записать так: 
если оно решается относительно производной, то его можно записать так: 
Если дифференциальное уравнение содержит ещё и производную второго порядка от искомой функции, то оно называется дифференциальным уравнением второго порядка:
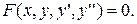
Основную трудность при решении задач, приводящих к дифференциальным уравнениям, представляет составление самих дифференциальных уравнений. Здесь нет универсального метода. Каждая задача требует индивидуального подхода, основанного на глубоком понимании соответствующего закона физики, химии, зоологии, биологии и умение переводить эти задачи на математический язык.
Рассмотрим задачи, приводящие к дифференциальным уравнениям.
Дифференциальные уравнения первого порядка с разделяющимися переменными.
Задача 1. Найти закон движения свободно падающего в пусто-
те тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна нулю. Скорость в этом случае выражается, как известно, формулой 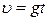 .
.
Решение.
Скорость переменного движения есть производная по времени. Поэтому  =gt (1.1)
=gt (1.1)
Из этого уравнения следует, что функция s есть первообразная функции gt. Следовательно,  или
или 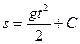 (1.2)
(1.2)
Для определения произвольной постоянной С используем то условие, что начало отсчёта пути совпадает с началом отсчёта времени, то есть при t = 0 s = 0. Подставляя эти значения в равенство (1.2), находим 0 = 0+С, то есть С = 0, и следовательно, окончательно получаем  .
.
Задача 2. (Об охлаждении тела). Скорость охлаждения тела в воздухе пропорциональна разности между температурой тела и температурой воздуха. Температура воздуха равна 200С. Известно, что в течение 20 минут тело охлаждается от 100 до 600С. Определить закон изменения температуры 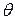 тела в зависимости от времени t.
тела в зависимости от времени t.
Решение.
Согласно условию задачи имеем  или
или
 (1.3)
(1.3)
где k>0 – коэффициент пропорциональности и x = 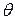 - 20.
- 20.
Разделяя в уравнении (1.3) переменные и затем, интегрируя, получаем 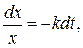
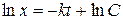 ,
,
что после потенцирования даёт  .
.
Для определения С используем начальное условие x = 80 при
t =0:

Следовательно, 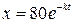 или
или  откуда
откуда 
Коэффициент пропорциональности k определяем из дополни - тельного условия: при t = 20, 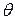 = 60. Отсюда 60=20+80
= 60. Отсюда 60=20+80 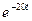 или
или
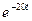 =
=  и, следовательно,
и, следовательно,  .
.
Итак, искомая функция  .
.
Задача 3. (О движении моторной лодки). Моторная лодка движется в спокойной воде со скоростью 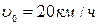 . На полном ходу её мотор выключается и через 40 с после этого скорость лодки уменьшается до
. На полном ходу её мотор выключается и через 40 с после этого скорость лодки уменьшается до 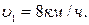 Сопротивление воды пропорционально скорости движения лодки.
Сопротивление воды пропорционально скорости движения лодки.
Определить скорость движения лодки через 2 мин. после остановки мотора.
Решение.
На движущуюся лодку действует сила сопротивления воды
 ,
,
где 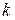 >0 – коэффициент пропорциональности.
>0 – коэффициент пропорциональности.
С другой стороны по второму закону Ньютона 
и, значит,  или
или 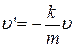 .
.
Решим это дифференциальное уравнение, разделяя переменные и интегрируя, получим:
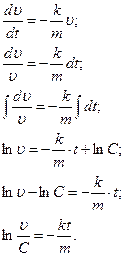
После потенцирования получаем:

Найдём С, используя начальное условие 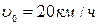 при t = 0:
при t = 0:

Поэтому 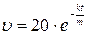 .
.
Теперь, используя дополнительное условие – при t = 40c = 
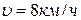 - получаем
- получаем  или
или 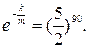
Следовательно,  .
.
Отсюда искомая скорость равна:
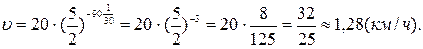
Задача 4. (О потере заряда проводником). Изолированному проводнику сообщим заряд 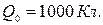 Вследствие несовершенства изоляции проводник постепенно теряет свой заряд. Скорость потери заряда в данный момент времени пропорциональна наличному заряду проводника. Какой заряд останется на проводнике по истечении времени t = 10 мин., если за первую минуту потеряно 100 Кл?
Вследствие несовершенства изоляции проводник постепенно теряет свой заряд. Скорость потери заряда в данный момент времени пропорциональна наличному заряду проводника. Какой заряд останется на проводнике по истечении времени t = 10 мин., если за первую минуту потеряно 100 Кл?
Решение.
Пусть в момент времени t заряд проводника равен  . Тогда скорость потери заряда в этот момент времени равна -
. Тогда скорость потери заряда в этот момент времени равна - 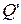 . По условию задачи
. По условию задачи  или
или  ,
,
где 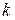 >0 – коэффициент пропорциональности.
>0 – коэффициент пропорциональности.
Решим последнее уравнение – это дифференциальное уравнение с разделяющимися переменными.
Разделив переменные и проинтегрировав, получим:

Потенцируя, последнее уравнение получим:

Используя начальное условие  при t = 0, найдём С:
при t = 0, найдём С:

Следовательно, 
Далее, используя дополнительное условие – при t = 1 мин.  , имеем
, имеем  ,
, 
Поэтому 
Следовательно, через 10 минут на проводнике останется заряд

Задача 5. (Заряд конденсатора). Конденсатор ёмкостью С включается в цепь с напряжением U и сопротивлением R. Определить заряд конденсатора в момент времени t после включения.
Решение.
Сила I электрического тока представляет собой производную от количества электричества q, прошедшего через проводник, по времени t  В момент t заряд конденсатора q и сила тока
В момент t заряд конденсатора q и сила тока  в цепи действует электродвижущая сила Е, равная разности между напряжением цепи U и напряжением конденсатора
в цепи действует электродвижущая сила Е, равная разности между напряжением цепи U и напряжением конденсатора 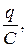 то есть
то есть 
Согласно закону Ома 
Поэтому 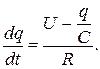
Отсюда 
или 
 ,
,
то есть, имеем дифференциальное уравнение с разделяющимися переменными.
Решим его:


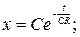
используя начальное условие x = СU при t=0, получим:  или
или 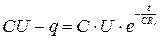
Откуда 
Задача 6. (Падение с парашютом). Составить закон движения парашютиста, масса тела которого равна m.
Решение.
При падении тел в безвоздушном пространстве их скорость равномерно увеличивается. Иначе обстоит дело, если падение происходит в воздухе. Будем для простоты считать, что сила сопротивления воздуха прямо пропорциональна скорости падения. Сила F, действующая на тело массы m, равна  (знак минус перед
(знак минус перед 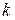 поставлен потому, что сила сопротивления воздуха направлена в сторону, противоположную направлению падения). Далее, так как по второму закону Ньютона
поставлен потому, что сила сопротивления воздуха направлена в сторону, противоположную направлению падения). Далее, так как по второму закону Ньютона  , где
, где 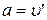 - ускорение, получаем уравнение:
- ускорение, получаем уравнение:

или
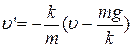
с начальным условием  при t = 0. Отсюда, вводя обозначение
при t = 0. Отсюда, вводя обозначение  , получаем
, получаем 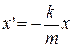 с начальным условием
с начальным условием  при t = 0, то есть имеем уравнение с разделяющимися переменными и начальным условием
при t = 0, то есть имеем уравнение с разделяющимися переменными и начальным условием  при t = 0.
при t = 0.
Значит  или
или 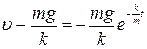 откуда
откуда 
По прошествии некоторого времени  станет очень малым числом и скорость падения будет почти в точности равна
станет очень малым числом и скорость падения будет почти в точности равна 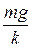 , то есть падение станет равномерным.
, то есть падение станет равномерным.
Теперь найдём закон движения парашютиста s = s(t). Для этого перепишем найденное выражение для скорости  в виде
в виде



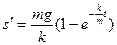 ,
,
откуда

что после интегрирования 
где С – производная постоянная. Для отыскания С заметим, что при t = 0 пройденный путь равен нулю, то есть при t = 0 имеем
S = 0.
Подставляя эти значения в последнее равенство, получаем
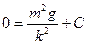 , т.е.
, т.е.  . Итак, закон движения парашютиста имеет вид
. Итак, закон движения парашютиста имеет вид 
Задача №7 (О прожекторе). Определить форму зеркала, обладающего тем свойством, чтобы все лучи, исходящие из источника света, помещённого в точке О на оси вращения, отражались бы зеркалом параллельно этой оси.
Решение.
Для решения задачи будем рассматривать плоское сечение зеркала, проходящее через ось вращения. Поместим источник света в начале координат, и пусть ось вращения совпадает с осью Ох (см. рис. 1). Обозначим через  угол, образованный осью Ох и касательной AS в произвольной точке сечения М (х; у).
угол, образованный осью Ох и касательной AS в произвольной точке сечения М (х; у).
|


Наша цель найти форму сечения, то есть зависимость координаты у от координаты х: у=у(х). Ломанная ОМТ изображает путь луча, исходящего из источника света в точке О и отражающегося в точке М от поверхности зеркала параллельно оси Ох. Проведём нормаль МN и опустим из точки М на ось Ох перпендикуляр МР. Так как  (угол падения равен углу отражения), имеем
(угол падения равен углу отражения), имеем 
 .
.
Следовательно,  NOM – равнобедренный и поэтому ОМ = ОN. Кроме этого, по построению
NOM – равнобедренный и поэтому ОМ = ОN. Кроме этого, по построению  . Можно переходить к составлению дифференциального уравнения:
. Можно переходить к составлению дифференциального уравнения:
ОN = РN – PO, PN= ytg  , PO = -x, ON=OM=
, PO = -x, ON=OM=  ,
,
ON = ytg  + x =
+ x =  .
.
Учитывая геометрический смысл производной:  , получаем для определения зависимости у от х дифференциальное уравнение первого порядка
, получаем для определения зависимости у от х дифференциальное уравнение первого порядка
 .
.
Для нахождения решения уравнения преобразуем его следующим образом. Умножаем обе части равенства на 2dx:
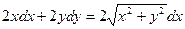 или
или 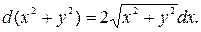
Подстановкой  приводим уравнение к уравнению с разделяющимися переменными
приводим уравнение к уравнению с разделяющимися переменными 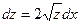 .
.
которое преобразуется к виду 
Отсюда находим  .
.
Заменяя переменную z её выражением через х и у, получаем

Упрощая полученное уравнение возведением в квадрат обеих его частей, получаем 
Таким образом, искомая кривая – парабола с параметром р = С и вершиной, лежащей на расстоянии  влево от начала координат (см. рис. 2). Следовательно, искомая отражательная поверхность – параболоид вращения.
влево от начала координат (см. рис. 2). Следовательно, искомая отражательная поверхность – параболоид вращения.
Линейные дифференциальные уравнения первого
Порядка.
Задача №1.
Скорость v, путь s и время t связаны уравнением  . Найти закон движения, если при t = 0 s = 2.
. Найти закон движения, если при t = 0 s = 2.
Решение:
Так как 
 ,
,  то подставляя это значение v в данное
то подставляя это значение v в данное  уравнение, получаем дифференциальное уравнение движения:
уравнение, получаем дифференциальное уравнение движения:

или 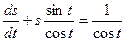 - это линейное дифференциальное уравнение первого порядка.
- это линейное дифференциальное уравнение первого порядка.
Решим его методом Бернулли, применив подстановку  , где
, где  ,
, 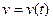 ;
;  , получаем
, получаем 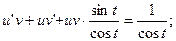
Сгруппировав члены, содержащие u и вынеся за скобки общий множитель, получим

Выражение в скобках приравняем к нулю:


Для отыскания u имеем уравнение:


По условию при t=0 s=2 и поэтому С=2. Таким образом, искомый закон движения 
 .
.
Задача2.
В помещении для крупного рогатого скота работают 2 вентилятора, каждый из которых в минуту доставляет по 60м3 чистого воздуха, содержащего 0,01% углекислоты. Полагая, что в коровнике объёмом 1600м3 с начальным содержанием углекислоты в 0,2% находится 120 коров, каждая из которых выдыхает в минуту 0,1м3 воздуха с 5% углекислоты, определить наличие углекислоты в 1м3 воздуха после двухчасового содержания животных в помещении.
Решение.
Пусть содержание углекислоты в 1м3 воздуха в момент времени t есть y(t) (в дальнейшем y). Скорость изменения концентрации равна приращению углекислоты 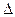 у, делённому на соответствующий промежуток времени
у, делённому на соответствующий промежуток времени 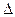 t;
t; 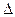 у определяется углекислотой:
у определяется углекислотой:
1) выделяемой при дыхании 120 животных,
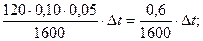
2) вводимой вентилятором на каждый кубометр,
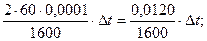
3) удаляемой за счёт работы вентиляторов
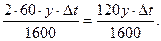
Следовательно,

Как видим, скорость изменения содержания углекислоты пропорциональна у. Перейдя к пределу при  , имеем:
, имеем:
 . Получено линейное дифференциальное уравнение. Находим его решение. Имеем:
. Получено линейное дифференциальное уравнение. Находим его решение. Имеем: 
Обозначим  тогда
тогда 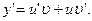 Примем следующее обозначение:
Примем следующее обозначение: 
 и подставим в последнее уравнение. В результате получим:
и подставим в последнее уравнение. В результате получим:
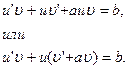
Положим  Тогда, учитывая, что
Тогда, учитывая, что  , имеем
, имеем

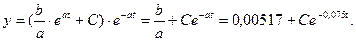
Определим произвольную постоянную С. При t = 0 согласно условию задачи у = 0,002. 
Окончательно имеем:

Если t = 120, то у 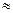 0,00517, так как второй член очень мал
0,00517, так как второй член очень мал

Таким образом, количество углекислоты в 1м3 (концентрация) увеличится в  раза и в дальнейшем увеличиваться уже не будет благодаря работе вентиляторов.
раза и в дальнейшем увеличиваться уже не будет благодаря работе вентиляторов.
Дата добавления: 2021-07-19; просмотров: 438; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
