NP -полные и NP-трудные задачи

Рассмотрим сводимость задач. Хотя сведение одних задач к другим является традиционной математической деятельностью, оно до работ С. Кука не было подвержено самостоятельному исследованию. Именно Куку принадлежит честь выделения этого понятия как центрального в теории полиномиальной сводимости.

Говорят, что задача Z₁сводится к задаче Z₂, если метод решения задачи Z₂можно преобразовать в метод решения задачи Z₁.

& Определение. Сводимость называется полиномиальной, если указанное преобразование можно осуществить за полиномиальное время.

 

& Определение. Если одновременно задача Z₁полиномиально сводится к задаче Z₂и Z₂полиномиально сводится к задаче Z₁, то задачиZ₁и Z₂ полиномиально эквивалентны.

 

& Определение. Задача называется NP-трудной если каждая задача из NP полиномиально сводится к ней.

 

NP-трудная задача имеет тот смысл, что эта задача не проще, чем «самая трудная в NP».

В классе NP выделяются NP-полные задачи.

 

& Определение. Задача называется NP-полной, если она входит в NP и каждая задача из NP полиномиально сводится к ней (т. е. является NP-трудной).

 

NP-полные задачи понимаются как самые трудные задачи из класса NP.

Класс NP-полных задач обладает следующими свойствами.

1. Никакую NP-полную задачу нельзя решить никаким известным полиномиальным алгоритмом.

2. Если бы удалось построить полиномиальный алгоритм для какой-нибудь NP-полной задачи, то это бы означало полиномиальную разрешимость каждой NP-полной задачи.

Основываясь на этих двух свойствах, многие высказывают гипотезу, что P NP. Практическое значение понятия NP-полной задачи лежит именно в широко распространенном мнении, что такие задачи по существу трудно решаемы. Следовательно, при их решении в худшем случае потребуется экспоненциальное количество времени и не будет возможности решить на практике такие задачи, за исключением очень малого числа индивидуальных задач.

 

& Теорема Кука. Задача выяснения выполнимости формулы логики высказываний, представленной в КНФ, является NP-полной.

 

Все приведенные ранее примеры NP-задач являются
NP-полными задачами. Список NP-полных задач в настоящее время содержит несколько сотен задач и продолжает пополняться. Многие вновь установленные NP-полные задачи печатаются в журналах.
В действительности о большей части задач комбинаторной оптимизации известна либо полиномиальная разрешимость, либо
NP-полнота, что является еще одним подтверждением гипотезы
P  NP.

 

Класс Е

Алгоритм имеет полиномиальную временную сложность, если существует полином p(x)такой, что на любом входном слове длины n алгоритм завершает вычисления после выполнения не более чем p(n) операций. Если такого полинома не существует, временная сложность считается экспоненциальной. Таким образом для них число операций возрастает быстрее значений любого полинома.

Кроме этого определения существует и второе определение: алгоритм имеет экспоненциальную временную сложность если его временная сложность имеет порядок не меньше, чем сaⁿ, где с > 0, a > 1 – постоянные. Иначе, временная сложность f(n) является экспоненциальной, если существуют постоянные с > 0, a > 1, что

                                                   саⁿ f(n)                                                   

для всех, кроме конечного числа значений n.

При первом определении, например задача, имеющая сложность порядка О( )О( 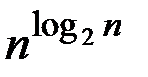) = О( 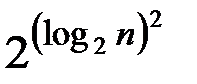) будет отнесена к задаче с экспоненциальной временной сложностью, а по второму определению – нет.

Отметим, что функция 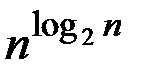 хотя и растет быстрее любого полинома, но растет медленнее, чем, например, 2ⁿ.

Большинство экспоненциальных алгоритмов – это просто варианты полного перебора. Экспоненциальные алгоритмы не считаются «хорошими», в отличие от полиномиальных алгоритмов, которые, считаются «хорошими». К экспоненциальным задачам относятся задачи, в которых требуется построить множество всех подмножеств данного множества, все полные подграфы некоторого графа или же все поддеревья некоторого графа.

Некоторые экспоненциальные алгоритмы весьма хорошо зарекомендовали себя на практике. Дело в том, что временная сложность определяется для худшего случая, а многие задачи могут быть не так плохи.

Для решения задачи линейного программирования существует так называемый симплекс-метод, который хотя и экспоненциален в худшем случае – уверено работает на практике для задач достаточно большого размера. Отметим, что для решения задачи линейного программирования Хачиян Л. Г. в 1979 г. предложил алгоритм эллипсоидов, который имеет полиномиальную временную сложность.

Метод ветвей и границ успешно решает задачу о рюкзаке, хотя этот алгоритм имеет экспоненциальную временную сложность.

Примеров экспоненциальных алгоритмов, успешно используемых на практике, мало. Более того даже для полиномиальных алгоритмов представляют практический интерес алгоритмы сложность которых имеет порядок n²или n³. Ясно, что алгоритмы со сложностью порядка n¹⁰⁰вряд ли будут практически используемы.

Интересно, что экспоненциальный алгоритм может оказаться при малом размере задачи более быстрым, чем полиномиальный, однако с ростом размера задачи полиномиальный становится более быстрым.

Экспоненциальная сложность задачи имеет следующие аспекты: – для отыскания решения требуется экспоненциальное время;

– искомое решение может быть настолько велико, что не может быть представлено выражением, длина которого была бы ограничена полиномом от длины входа.

Вторая ситуация возникает, например, если в задаче коммивояжера требуется найти все маршруты длины, не превосходящей заданной величины L. Может оказаться, что имеется экспоненциальное число маршрутов длины не превосходящей L.

 

 

Учебное издание

 

 

ПОРЕЧНЫЙ Сергей Сергеевич

ЖИТНИКОВА Наталья Ивановна

ШЕРЫХАЛИНА Наталия Михайловна

УРАКОВ Айрат Ренатович

 

ДИСКРЕТНАЯ МАТЕМАТИКА

 

Редактор Ф. Х. Гарипова

Компьютерная верстка Ф. Х. Гарипова

Оформление обложки О. М. Толкачева

 

Подписано в печать 00.03.2019. Формат 60´84 1/16.

Бумага офсетная. Печать плоская. Гарнитура Times New Roman.

Усл. печ. л. 0,0. Уч.-изд. л. 0,0.

Тираж 100 экз. (1-й завод – 1–31 экз.). Заказ №

ФГБОУ ВО «Уфимский государственный авиационный

технический университет»

Редакционно-издательский комплекс УГАТУ

450008, г. Уфа, ул. К. Маркса, д. 12.

 

---

Дата добавления: 2021-02-10; просмотров: 427; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!