Полиномиальные алгоритмы и задачи. Класс Р

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

& Определение. Алгоритм называется полиномиальным или имеющим полиномиальную временную сложность, если существует полином p(x)такой, что на любом входном слове длины n алгоритм завершает вычисления после выполнения не более чем p(n) операций.

Алгоритмы А1и А2, временные сложности которых равны, например, О(n^3/2) и О(n²log₂n) будут считаться полиномиальными, так как их сложности ограничены полиномами, т. е. имеют порядок не выше, чем О(n²) и О(n³)соответственно.

& Определение. Задача разрешима за полиномиальное время или полиномиально разрешима, если для нее существует полиномиальный алгоритм. При этом считается, что задача является «хорошей».

& Определение. Множество всех задач, для каждой из которых существует полиномиальный алгоритм, называется классом Р.

Среди полиномиальных алгоритмов быстрыми являются линейные алгоритмы, которые обладают сложностью порядка n, где n – размерность входных данных. К линейным алгоритмам относится школьный алгоритм нахождения суммы десятичных чисел, каждое из которых состоит из n цифр. Сложность этого алгоритма – О(n).

В класс Р кроме линейных задач попадают:

– умножение целых чисел. Школьный метод умножения 2-х
n-разрядных чисел имеет временную сложность порядка О(n²). Существует алгоритм Шенхаге–Штрассена умножения чисел (заданных в двоичной системе счисления) с меньшей сложностью, именно со сложностью порядка О(n log₂n log₂ log₂n).

– Умножение матриц. Обычный метод имеет порядок сложности О(n³). Существует более быстрый алгоритм умножения матриц – алгоритм Штрассена, который имеет сложность порядка
О( ).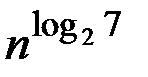

– Найти кратчайший путь на графе из n вершин и m ребер. Сложность алгоритма О(mn). Быстрое преобразование Фурье требует
О(n log₂n)арифметических операций.

& Определение. Задачи, для которых не существует полиномиального алгоритма, считаются трудно разрешимыми.

Рассмотрим пример определения сложности вычислений (алгоритма) на примерах.

Пример

v Пусть задано множество S, содержащее n действительных чисел. Требуется найти наибольший и наименьший элементы из S. Положим, что каждое одно сравнение двух любых чисел осуществляется за одинаковое время.

Один из возможных методов состоит в поиске сначала наибольшего элемента из S, а затем – наименьшего. Наибольший элемент можно найти, проводя n – 1сравнений, например по следующему алгоритму.

begin

MAX←произвольный элемент из S;

for все другие элементы х из S do

if x>MAX then MAX←x;

end.

В результате n – 1сравнений найдется наибольший элемент. Заметим, что не учитывается время на выборку элемента. Далее начинается поиск наименьшего элемента по аналогичному алгоритму. Если считать эти процедуры независимыми, то вновь потребуется n – 1сравнений. В итоге для нахождения наибольшего и наименьшего элементов из S потребуется 2n – 2сравнений.

Число необходимых сравнений можно уменьшить, если использовать принцип «разделяй и властвуй», который в теории алгоритмов называют еще стратегией дублирования.

Стратегия дублирования состоит в следующем. Пусть размер задачи (размер входных данных задачи) равен n. Разобьем задачу на две подзадачи размера n/2той же структуры, что и исходная задача. Если решения этих задач можно скомбинировать в решение исходной задачи, то получится эффективный алгоритм.

Рассмотрим, как стратегия дублирования дает ускорение для решения предыдущей задачи.

Примеры

v Положим, что число элементов множества S является степенью числа 2, т. е. n = 2^k, для некоторого k, k ≥1. Реализуем рекурсивный поиск, при котором множество S разбивается последовательно на два подмножества по следующей процедуре MAXMIN.

procedure MAXMIN(S):

1. if |S| = 2 then

begin

2. пусть S = {a,b};

3. return (MAX(a,b), MIN(a,b))

end

else

begin

4. разбить S на два равных подмножества S₁ и S₂;

5. (max1, min1)←MAXMIN(S 1);

6. (max2, min2)←MAXMIN(S 2);

7. return (MAX(max1, max2). MIN(min1, min2))

end

В этой процедуре сравнения происходят только на 3-м шаге, где сравниваются два элемента множества S из которых оно и состоит, и на шаге 7, где сравниваются max1 с max2 и min1 с min2. Пусть Т(n) – число сравнений элементов множества S. Очевидно, что Т(2) = 1.Если n > 2, то Т(n) – общее число сравнений, произведенных в двух вызовах процедуры MAXMIN (строка 5 и 6), работающих на множествах размера n/2и еще два сравнения в строке 7. Таким образом,

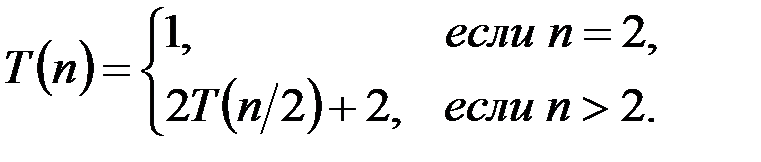. (П1.1)

Решением данных рекуррентных уравнений служит функция Т(n) = (3/2)n – 2. Таким образом, вместо 2n – 2 сравнений получили (3/2)n – 2 сравнений чисел, т. е. на (n/2)сравнений меньше.

v Рассмотрим второй пример. Пусть требуется умножить два n разрядных двоичных чисел. При традиционном алгоритме требуется О(n²)битовых операций. Применим стратегию дублирования и разобьем числа х и у на две равные части:

x =	a	b
y =	c	d

Считаем, что n есть степень числа 2. Тогда

xy = (a2ⁿ^/2+ b)(c2ⁿ^/2+ d) = ac2ⁿ + (ad + bc)2ⁿ^/2+ bd. (П1.2)

Равенство (П1.2) дает способ вычисления ху с помощью четырех умножений (n/2) разрядных чисел и нескольких сложений и сдвигов (умножений на степень числа 2). Можно достичь вместо О(n²) битовых операций О( ) ≈ О(n^1,59)битовых операций. Здесь число разбивалось на два блока. Разбивая эти числа на большее число блоков можно получить, что умножение двух чисел имеет сложность О(n log₂n log₂ log₂n)для алгоритма Шенхаге–Штрассена.

Абстрактной моделью полиномиального алгоритма является детерминированная машина Тьюринга, которая в каждый данный момент времени находится в строго определенном состоянии, за один шаг она совершает одно из некоторого конечного множества действий. Затем она переходит в следующее состояние и все начинается вновь, пока не придет к ситуации останова.

NP класс

Наиболее простыми считаются полиномиальные задачи, т. е. задачи класса Р.

Другим, возможно более широким, «сложностным классом» является класс NP. Эта аббревиатура обозначает выражение «разрешимых на Недетерминированной машине Тьюринга за Полиномиальное время».

Класс NP стали впервые изучать Эдмонде, Кук и Кири. Оказалось, что многие известные задачи принадлежат к NP классу.

В обычных машинах Тьюринга (их называют детерминированными, чтобы отличать от недетерминированных) новое состояние, в которое машина переходит на очередном шаге, полностью определяется текущим состоянием и тем символом, который обозревает головка на ленте.

В недетерминированных машинах Тьюринга для каждого состояния может быть несколько следующих состояний, в соответствии с функцией перехода. И в каждом следующем состоянии запускается новая копия данной машины Тьюринга.

Недетерминированность лучше всего понять, рассматривая алгоритм, который производит вычисления до тех пор, пока не доходит до места, в котором должен быть сделан выбор из нескольких альтернатив. Детерминированный алгоритм исследовал бы сначала одну альтернативу, а потом вернулся для рассмотрения следующей альтернативы. Недетерминированный алгоритм может исследовать все альтернативы одновременно, «копируя», в сущности, самого себя для каждой альтернативы. Все копии работают независимо. Если копия обнаруживает, что данный путь безрезультатный, то она прекращает выполняться. Если копия находит требуемое решение, она объявляет об этом, и все копии прекращают работать.

& Определение. NP класс – классзадач, которые можно решить недетерминированными алгоритмами, работающими в течение полиномиального времени.

Чтобы доказать, что некоторая задача принадлежит классу NP, достаточно построить недетерминированный алгоритм (алгоритм недетерминированной машины Тьюринга), который решает эту задачу за полиномиальное время.

Пусть имеем, например, задачу выяснения существования в орграфе гамильтонового цикла, длина которого меньше или равна M.

Рассмотрим следующий алгоритм.

begin

v₁←1 {Пункт отправления}

S ←{2,3,…,n}{Множество вершин, которые нужно посетить}

Длина пути ←0{Общая длина пути}

nv←1 {Число пройденных вершин}

{Пусть преемник (v _nv) обозначает допустимое, (не содержащее паразитных циклов) множество вершин, в которые можно попасть из v _nv}

while преемник (v _nv) do

begin

v _nv _–₁ ←ВЫБОР (преемник(v _nv));

nv ← nv+1;

Длина пути ←Длина пути+длина дуги (v _nv _–₁, v _nv)

end

if nv = n and Длина пути M then успех

else неудача

end

В этом алгоритме рассмотрение каждого варианта, т. е. последовательности соединенных дугами вершин v₁, v _i₂, v _i₃,…,v _in требует n шагов. Следовательно, каждая процедура ВЫБОР(иначе каждая копия алгоритма просмотра одного пути) работает не более, чем полиномиальное время, точнее имеет сложность порядка О(n). Таким образом, задача выяснения существования в орграфе гамильтонового цикла, длина которого меньше или равна M, является NP задачей.

Детерминированная машина Тьюринга является частным случаем недетерминированной машины Тьюринга (которая не имеет копий), поэтому имеем, что 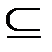P NP.

Вопрос о том, будет ли P = NP,является открытой проблемой теории сложности. Широко распространено мнение, что P 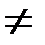NP, следовательно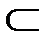, P NP.

Примеры

v Примеры задач из класса NP:

1) выяснение выполнимости формулы логики высказываний, записанной в КНФ;

2) нахождение целочисленных решений системы линейных

уравнений;

3) задача распознавания простого числа;

4) выяснение гамильтоновости графа;

5) задача коммивояжера;

6) размещение обслуживающих центров (телефон, телевидение, срочные службы) для максимального числа клиентов при минимальном числе центров;

7) оптимальный раскрой (бумага, стальной прокат, отливка), оптимизация маршрутов в воздушном пространстве, инвестиций, станочного парка;

8) составление расписаний, учитывающих определенные условия;

9) оптимальная загрузка емкости (рюкзак, поезд, корабль, самолет) при некоторых условиях;

10) динамическое распределение памяти. Раскроем эту проблему. Пусть заданы А – множество элементов данных, размер s(a) 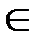N, для каждого элемента данных а А, время поступления r(a) N и время d(a) N окончания работы с элементом данных а 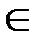А, положительное целое число D – размер области памяти.

Вопрос. Существует ли для множества элементов данных допустимое распределение памяти? Иначе говоря, существует ли такая функция σ: А→{1,2,3,…}, что для каждого элемента а А интервал

l(a) = [σ(a),σ(a) + s(a) – 1]

содержится в [1, D], причем для любых а, а* 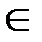А, если l(a)∩ l(a*) , то либо d(a) r(a*),либо d(a*) r(a).

В случае, когда размеры всех элементов данных одинаковы, то задача решается за полиномиальное время.

Дата добавления: 2021-02-10; просмотров: 175; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!