Краткий анализ основ геометрий 27 страница

⇐ ПредыдущаяСтр 27 из 48Следующая ⇒

Однако эти отношения не являются следствием деления отрезка на доли, и оказываются не отношениями долей, а пропорциями некоторых неизвестных безразмерностных чисел, отнесенных к делению отрезка. Числа же могут быть не причастными к делению отрезка в крайнем и среднем отношении. Их принадлежность к геометрии золотого сечения еще следует доказать нахождением геометрических пропорции длин долей АВ и ВС. И потому, при алгебраическом решении (3.20) со степенями р = 1, 2, 3, … получаемый ряд 2; 1,618; 1,465;1,380; … не имеет никакого отношения к золотой пропорции даже при наличии в нем х = 1,618… .

Тем не менее, в настоящее время, считается возможным обобщить их, на основе не имеющего геометрического смысла алгебраического уравнения (3.22), в единый класс золотых пропорций и считать “обобщенными золотыми р - пропорциями”. Покажем, что корректно этого сделать не удается и ряд (3.23), за исключением одного числа t₁, имеющего численную но не размерностную величину равную Ф, не образует обобщенных золотых пропорций. К тому же использование t ^р не обусловливает вычисление длин долей а и с, и построение треугольников типа (3.18) или других геометрических фигур, а члены данного (3.23) обобщения не отвечают критериям чисел Фибоначчи или Люка.

Деление отрезка в золотой пропорции приводит, как показано выше, к появлению уравнения прямоугольного золотого треугольника. Следовательно, по аналогии, и делению по формуле (3.22) должно соответствовать некое уравнение, отображающее геометрическое смысл этого деления. Получим его для р² и р³, исходя из (3.20):

с^р+1= аd^р

при р² имеем: с³ = аd², (3.24)

при р³ имеем: с₁⁴ (?) = а₁d³. (3.25)

Уравнение (3.24) приравнивает объем куба к объему некоего “бруска”, а уравнение (3.25) геометрически бессмысленно. Но алгебраически все верно. Решаем их подставляя соответствующие значение х в (3.24) и (3.25) получаем: с = 2,146а, с₁ = 2,268а₁. Т.е. длина долей остается неизвестными, а образуемая пропорция может быть отнесена не только к долям отрезка, а к любым пропорциональным 1,464 и 1,380 случайным числам.

Предположим однако, по аналогии с золотым сечением, что, например, t ₃ как доля отрезка полученная при р = 3, образует прямоугольный треугольник в той же пропорции, что золотой треугольник, т.е. а³ = b² = с¹. Или в численном выражении: 1,175; 1,38; 1,621 и проверим предположение.

(1,175)² + (1,380)² = (1,38) + (1,904) = 3,287 ¹ (1,621)² = 2,628

Итак, численная величина t ₃ = 1,38 с приданием ей функции долей-отрезков не образует прямоугольного треугольника, что указывает на отсутствие у числа 1,38 золотых качеств.

Другой критерий: при последовательном делении или умножении 1 на золотое число 1,618 образуется греческий ряд чисел

…; 0,056;0,090;0,146; 0,236; 0,382;0,618;1,000;1,618;2,618; (3.26)

в котором выполняется правило Фибоначчи сложения двух последовательных чисел с образованием следующего за ними числа ряда:

0,056 + 0,090 = 0,146 + 0,236 = 0,382 и т.д.

Образуем, например, из числа 1,38 аналогичный ряд и проведем операцию сложения двух любых последовательных чисел:

…; 0,1998; 0,2757; 0,3805; 0,5251; 0,7246; 1,000; 1,380;1 ,904; … (3.27)

0,3805 + 0,5251 = 0,9056 ¹ 0,7246,

или

0,7246 + 1,000 = 1,7246 ¹ 1,380 и т.д.,

равенства слагаемых последующему числу не получается, что также свидетельствует об отсутствии у t ₃ золотых качеств. И так по всем t _р , образуемым числами “обобщенных золотых пропорций”.

Наконец, главным свидетельством отнесения образуемых чисел к золотым является получение, при делении одного из них на другое, золотого числа Ф с тем большей точностью, чем дальше от начала ряда берутся числа. Все числа греческого ряда этому критерию соответствуют, поскольку получены именно через золотое число Ф. Числа рядов, полученных из “обобщенных золотых р-сечений” не соответствуют и этому критерию. И можно сделать вывод: золотая пропорция в виде (3.13) единственна в математике и потому не может быть обобщена. Надо отметить, что ряд (3.27) как и (3.26) является геометрической прогрессией и как таковой имеет прямое отношения к золотому ряду, но в неявном виде (об этом разговор отдельный). Однако в виде (3.27) те золотые качества, которые имеются у греческого ряда, он не проявляет и потому к золотой пропорции не принадлежит.

И можно сделать вывод: Деление отрезка в крайнем и среднем отношении производится геометрическим методом с сохранением за долями – отрезками формальных и размерностных качеств, с соблюдением качественных переходов от геометрии к алгебре и обратно и является единственной операцией деления, не поддающейся обобщению.

Гармония золотых пропорций

В архитектуре известно, что объекты, построенные с соблюдением золотых пропорций, обладают высокими эстетическими качествами и гармоничностью своих частей. Для древних греков, широко применявших золотые пропорции в проектировании своих сооружений, условием гармонии или устойчивого совершенства являлось присутствие пропорциональной связи между всеми элементами сооружения. Да и само слово «гармония» означает в переводе с древнегреческого – «связь». А гармоничное сочетание частей в целом выражается через числовое соотношение – пропорции. Можно сказать, что гармония это система качеств, пропорционированная природе. Или, другими словами, разнообразие элементов (предметов, фигур, чисел и т.д.), пропорционированное природным параметрам. Что же обусловливает появление гармонии? Какие качества свидетельствуют о ее наличии?

К гармонически выдержанным искусственным или числовым системам, отображающим природные процессы, можно отнести совокупность следующих свойств:

Пропорционирование элементов золотому числу.

Единство целого в многообразии.

Всеобщая взаимосвязь между элементами.

Структурность одного отношения, позволяющая восстанавливать систему по минимуму исходных данных.

Отсутствие случайных операций и элементов в системе.

Степенная и арифметическая комбинаторика элементов.

Память числа (каждый элемент помнит о наличии остальных). И т.д.

Все эти свойства можно и не перечислять, ибо они заложены в пропорционировании по золотому числу. Но, к сожалению, ученые еще не научились понимать и использовать золотое сечение так, чтобы его можно было применять ко всем природным явлениям. Мы не собираемся рассматривать всю гамму взаимосвязей гармонических систем, некоторые их аспекты будут отображены в дальнейшем. Покажем только элементы гармонии в геометрии и для наглядности приведем из Библии пример восстановления основных параметров Храма, построенного царем Соломоном для Господа, точные размеры которого к настоящему времени утеряны. А сейчас вернемся к ряду 1.

Архитектор А. Пилецкий, изучая числовые системы архитектурного пропорционирования, обратил внимание на то, что числам рядов Фибоначчи свойственна многовариантная слагаемость членов с получением результатирующего числа в их же системе [25]. Например:

3 + 5 = 8; 3 + 5 + 13 = 21; 3 + 5 + 13 + 34 = 55 и т.д.

Эти арифметические комбинаторные свойства рядов являются первым признаком гармоничности создаваемой системы. И система имеет тем большую гармонию, чем более высокими комбинаторными свойствами обладают ее члены, чем лучше они связаны между собой и чем более они отображают природу. Возможно, поэтому природа, в том числе и живая, постоянно использует в своей структуре и компоновках элементы золотых пропорций и ряды типа Фибоначчи. И числовая система А. Пилецкого из строк Фибоначчи и столбцов Паскаля (таблица 3), обладает более высокими комбинаторными возможностями, чем отдельные ряды Фибоначчи. В ней взаимозависимость между членами рядов распространяется на все поле. Покажем это на примере получения одного и того же результата слагаемыми из разных рядов (табл. 3):

3 + 52 = 55; 4 + 5 + 13 + 16 + 17 = 55;

2 х 3 + 2 х 6,5 + 2 х 8 + 2 х 10 = 55 и т.д.

Возможны не только действия сложения и вычитания чисел, но и пропорционирование многих из них. Однако наивысшими комбинаторными «способностями» обладают матрицы типа русских матриц, фрагмент одной из которых показан ранее (матрица 1). В них проявляется первый признак гармоничности – взаимное степенное пропорционирование чисел всего поля. Именно это свойство заложено в структуру древнерусских саженей [23] и оно же отображается в проективной геометрии как сложное отношение четырех точек. Это настолько важное, для понимания геометрии и физики, отношение, что мы, опираясь на [26], вкратце изложим его получение:

«Пусть в некоторой плоскости имеется окружность и точка М вне - ее (рис. 46). Из этой точки (даже если она бесконечно удалена) можно провести две касательные. Точки касания определяют единственную прямую m. Точка М становится полюсом прямой m, а прямая m – полярой точки М. Через полюс и центр окружности проведем прямую. Она пересечет окружность в точках А и В, а поляру в точке N. Таким образом, на этой прямой получатся две пары точек: одна пара на окружности, а вторая полюс и точка на поляре. Оказывается, отношение длин отрезков АN и NВ равно отношению длин отрезков АМ и МВ. Его можно записать в виде равенства:

ô AN ô / ô NB ô = ô AM ô / ô MB ô ,

или равносильного ему равенства

( ô AN ô / ô NB ô ): ( ô AM ô / ô MB ô ) = 1 - const.» (3.28)

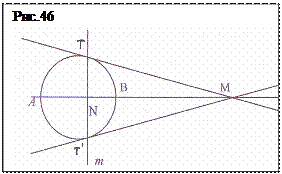Принято говорить, что точки N и М делят отрезок АВ гармонически или, что на прямой имеется «гармоническая четверка точек»: А, N, В, М».

Сложное отношение (3.28) - основное отношение гармонического пропорциониро-вания в проективной геометрии. Оно пронизывает все девять проективных геометрий. Но оно избыточно. Для построения гармоничес-ких систем всех элементов проективной геометрии нужно не четыре, а три точки. Те самые три точки, которые появляются при делении отрезка в крайнем и среднем отношении. Три точки необходимо и достаточно для построения гармоничной бесконечной системы отрезков на рис. 46. Три числа необходимы и достаточны для построения каждой (кроме объемной) золотой матрицы. Три свойства необходимы и достаточны для нахождения всех параметров любой отдельной физической системы. На числе три базируется вся теория физической размерности. Да и в православной религии, как и во многих других, число три, отображающее духовную взаимосвязь между действующими личностями: Отец, Сын и Дух Святой, занимает очень значимое положение, отображая всю систему духовного взаимодействия.

Все начинается с числа З. (Вспомним пословицу: «Бог троицу любит».) И не потому, что оно простое и, находясь в натуральном ряду после двух, в некоторых случаях имеет значение «много», а потому, что число два создает размерность, обусловливая появление эталонного размера, а число три соразмерность, обусловливая появление гармонии в системе. Для нахождения гармоничных золотых фигур проективной геометрии начнем построение с деления отрезка в крайнем и среднем отношении методом, например, двумерного квадрата (рис. 47). Возьмем отрезок ВА произвольной длины и проведем деление в крайнем и среднем отношении методом двойного квадрата. Порядок деления отрезка показан пунктиром. В результате деления получили на прямой три точки В, N, А и два отрезка АN и ВN, отношение которых АN / NВ = 1,618, длина же в см АN = 2,057 см, а ВN = 1,272 см. Прямая ТТ¢, перпендикуляр, восстановленный из точки N, становится полярой четвертой, отсутствующей на чертеже точки М. Обозначения соответствуют рис. 46. 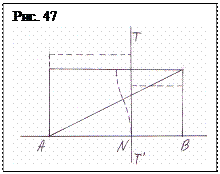Перенесем три точки на новую прямую (рис. 48) и определим для них четвертую точку – полюс М. Полюс можно отыскать двумя способами: геометрическим и проективным. На рис. 48 показаны оба способа. Геометрическим способом делим отрезок АВ пополам и из центра циркулем проводим окружность, у которой АВ – диаметр. К точке пересечения окружности с полярой ТТ¢ проводим касательную МД. Ее пересечение в точке М с продолжением диаметра и будет полюсом - четвертой гармонической точкой. Построение проективное: Проводим из точки В две «случайные» прямые 1 и 2 (все обозначены пунктиром). Из точки N проводим прямую 3 до пересечения с прямой 1 в точке 6. Из точки А проводим в точку 6 прямую 4, и из нее же через точку пересечения прямых 2 и 3, проводим прямую 5. Через точки пересечения прямых 1 и 5, 2 и 4 проводим прямую МК, которая и пересечет продолжение диаметра АВ в той же точке М, и снова получаем четвертую гармоническую точку

– полюс. Проведя прямые АL и ВL получим вписанный прямоугольный треугольник АLВ составленный из двух подобных треугольников ВLN и АLN. Зная длину отрезков АN = 2,058 см и ВN = 1,272 см, определяем длины всех отрезков между найденных точек. Получаем: АВ = 3,33 см, NL = 1,618 см, ВL = 2,058 см, АL = 2,618 см, МВ = 5,39 см, МL = 6,85 см, АМ = 8,72 см. Все модули этих отрезков входят в восходящую ветвь русского ряда золотых чисел [23]:

1; 1,272; 1,618: 2,058; 2,618; 3,330; 4,236; 5,388; 6,854; 8,718; … (3.29)

Ряд (3.29) можно разложить на ряд Пилецкого:

…; 1,000; 1,618; 2,618; 4,236; 6,854; …

…; 1,272; 2,058; 3,330; 5,388; 8,718; …

получив фрагмент удивительной многобазисной русской матрицы.

Все образовавшиеся точки связаны отрезками, модули длин которых кратны золотому числу Ф = 1,618 и, следовательно, эти точки квантованы гармонически через Ф, которая и лежит в основах проективных геометрий. Построение точек можно продолжить используя систему найденных точек и на прямой и на поляре, например, проведя из точки А радиусом АВ дугу до пересечения с полярой. Отсеченная часть поляры будет иметь длину - 2,618 см, длина же касательной от этой точки до точки пересечения М¢¢ будет равна 4,236 см, и т.д.

Следует обратить внимание на то, что с возрастанием количества искомых точек их сложное пропорционирование отображается отрезками не только на прямой, на которой расположен отрезок АВ, но и сопровождается пропорционированием поляры по золотому числу. И ее также можно использовать для нахождения последующих гармонических точек.

Количество взаимосвязанных точек бесчисленно и путем построения, как геометрическим методом, так и методами проективной геометрии можно получить любое их гармоничное количество, начиная с трех первых.

Нахождение проективными методами геометрической золотой пропорции обусловливает появление сложных отношений не только между отрезками и точками проективной геометрии подобных (3.28), но и между модулями этих отрезков. Причем пропорционирование проявляет себя в степенной форме, образуя своеобразную геометрическую степенную комбинаторику, связывающую в единую систему все многообразие получаемых проективными методами модулей. Приведем несколько примеров:

ВL / АN = 1 - const. АВ / ВN³ = 1 - const. ВL² × МВ × АL / АВ⁴ × ВN = 1 - const.

М L² / АВ ² × NL² × В N²− const. М L² = АВ ² × NL² × В N²-const. И т.д. (3.30)

Основой геометрической степенной комбинаторики, образующей гармонические системы, включая систему физической размерности, является в своей совокупности класс русских матриц. Именно всеобщая взаимосвязь членов числового поля русских матриц становится качественной основой математической гармонии и описывает гармонию природных, геометрических и физических систем.

Это свойство гармоничных фигур и комбинаторика, степенная и арифметическая, чисел обусловливает, например, возможность восстановления отдельных элементов фигур или чисел в том случае, когда они оказываются утраченными или еще не были найдены. Естественно, такое возможно только в том случае, когда построение фигур, или уравнения, связывающие утраченные числа, базируются на золотых пропорциях. Ибо золотые пропорции это гармоническая система, обеспечивающая взаимосвязь всех своих членов. Приведем пример восстановления размеров храма Господа, построенного Соломоном. Предварительно отметим, что существуют соизмерительные инструменты – древнерусские сажени в количестве 15, восстановленные А. Пилецким, названная им «Всемером», и базирующиеся на золотом числе. Операции соизмерения, проводимые в древности с комплексом древнерусских инструментов – саженей, до сих пор остается непонятными не только для широкой общественности, но и для специалистов, реставрирующих древние сооружения и храмы. Не ясно, почему их было много? Зачем было использовать для разметки объекта в высоту одни сажени в ширину другие и в длину третьи? Почему они несоразмерны между собой? И т.д. Логика длины требовала применения единообразного измерительного инструмента. И таким инструментом стал метр. Однако метр эталон для отделения частей от целого. Им невозможно соизмерять. Он годится только для измерения найденных пропорций. Проектировать и строить на основании метра нельзя.

Воссоздание А. Пилецким «Всемера» из 15-ти древнерусских саженей - важнейшее историческое, культурное и архитектурное открытие ХХ века (см. приложение 2.). Особенность, отличающая древнерусские сажени от всех других инструментов, заключается в том, что получение их долей происходило путем раздвоения (делением пополам). Никакого дробления элементов на части более 2-х не допускалось. Всего сажень включала шесть элементов (долей), и последний – вершок был 32-ой частью сажени. Каждый элемент имел двойное название. Например, сажень великая, локоть греческий или пядь церковная, поскольку ни один из них не был равен по длине никакому другому. И только элементы малой сажени не имеют второго названия. К тому же каждая сажень по воле зодчего могла «возрастать» по длине в полтора, два и два с половиной раза. Естественно, что части этих саженей тоже пропорционально увеличатся. В приложении 3 приведена таблица длин саженей и локтей в метрических величинах (в см.) с округлением до 4-х знаков.

Последовательное деление саженей надвое производилось для того, чтобы в любой части строительного объекта укладывалось только целое число саженей или их элементов. Причем разбивка плана каждого объекта производилась четным числом саженей. Объем объекта формировался, начиная с высоты – от Бога, в котором укладывалось четное число одной сажени, затем разбивалась ширина четным числом других саженей и, наконец, длина аналогичным числом третьих саженей. Разметка внутренних объемов объекта производилась так же, но уже элементами саженей и чем меньше было помещение, тем меньшая часть сажени использовалась.

Дата добавления: 2021-02-10; просмотров: 92; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 22 23 24 25 262728 29 30 31 Следующая ⇒

Мы поможем в написании ваших работ!