Метод интегрирования подстановкой (замена переменной).
Часто интеграл можно значительно упростить, сделав замену переменной. Такой метод интегрирования заключается в том, что при помощи подстановки переменная интегрирования заменяется на функцию от другой независимой переменной.
Пусть нужно найти  .
.
Сделаем замену переменной  , где
, где  – функция, имеющая непрерывную производную. Тогда
– функция, имеющая непрерывную производную. Тогда  .
.
Получим формулу интегрирования подстановкой:
 .
.
Эта формула также называется формулой замены переменной в неопределенном интеграле. После вычисления интеграла правой части формулы следует вернуться к старой переменной интегрирования x.
Иногда бывает удобнее сделать подстановку в виде  . Как это сделать мы увидим далее в процессе решения примеров.
. Как это сделать мы увидим далее в процессе решения примеров.
Примеры.
1. Найти 
Решение.
Сделаем замену 
Тогда 
 , и
, и
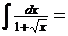

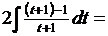

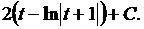
Возвращаясь к переменной x, получаем
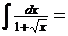

Можно использовать краткую запись, выделяя замену переменной и выкладки, связанные с ней, вертикальными линиями. Запись данного примера будет выглядеть так:



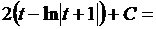

2. Вывести формулу для табличного интеграла 
Решение.
Введем новую переменную 
Такая подстановка называется подстановкой Л. Эйлера. Выразим переменную x через t. Для этого проделаем следующие выкладки:




Найдем dx: 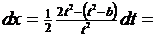

Выразим  через t:
через t:
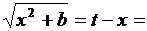

Подставим dx и  под знак интеграла и получим
под знак интеграла и получим





Замечание. Так как этот интеграл часто встречается в приложениях, а нахождение его трудоемко, мы включили его в основную таблицу интегралов.
|
|
|
3. Найти 
Решение.
Сделаем замену  . Тогда
. Тогда 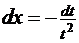 ,
, 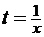 .
.


Теперь нужно вернуться к старой переменной. Получим

4. Решим предыдущий пример другим способом.
Сделаем замену  . Тогда
. Тогда 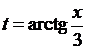 и
и 
Применяя тригонометрическую формулу
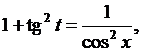
получим

Следовательно,

 .
.
Мы видим, что при различных подстановках получены разные по виду результаты. На самом деле можно доказать, что результаты одинаковы.
1. Найти 
Решение.
Выделим в знаменателе полный квадрат

и сделаем замену  тогда
тогда
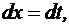
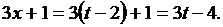
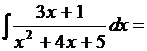




Примеры для самостоятельного решения
| Задание | Ответ | Подстановка |
1. 
| 
| 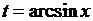
|
2. 
| 
| 
|
3. 
| 
| Выделить полный квадрат в подкоренном выражении. |
4. 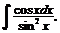
| 
| |
5. 
| 
| |
6. 
| 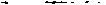
| |
7. 
| 
| |
8. 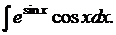
| 
| |
9. 
| 
| 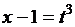
|
Приложение
Алгебраические выражения
 ;
;
 ;
;
C войства степеней

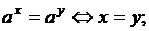


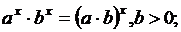
Логарифмы
(  )
)
 ,
, 
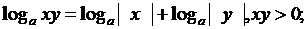

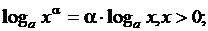





Тригонометрические функции


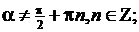

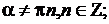

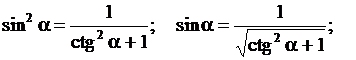





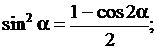
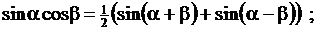
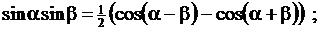


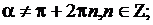


ЛИТЕРАТУРА
1. Берман Н.Г. Сборник задач по курсу математического анализа. – СПб.: Специальная литература, 2000.
|
|
|
1. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. – М.: Наука, 1984.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1. – М., 2004.
3. Пискунов Н.С. Дифференциальное и интегральное исчисление для
ВТУЗов. Т. 1,2. – М.: Наука, 1996.
4. Письменный Дм. Конспект лекций по высшей математике. Полный курс. – М.: Айрис-Пресс, 2011.
5. Васильева Н.И., Непомнящая Е.Ю., Филиппова А.Ф. Неопределенный интеграл. Учебное пособие.– СПбГУКиТ. 2007.
Оглавление
Стр.
§1. Первообразная и неопределенный интеграл………………………………..3
§2. Вычисление интегралов с помощью таблицы интегралов и их свойств….6
§3. Интегрирование методом подведения под знак дифференциала………..10
§4. Интегрирование по частям………………………………………………….15
§5. Метод интегрирования подстановкой (замена переменной)……………..19
Приложение………………………………………………………………………23
Литература……………………………………………………………………….25
Дата добавления: 2021-01-20; просмотров: 70; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
