Вычисление интегралов с помощью таблицы интегралов и их свойств
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
КИНО И ТЕЛЕВИДЕНИЯ»
Кафедра математики и информатики
Н.И. Васильева, Е.Ю. Непомнящая
МЕТОДЫ
ИНТЕГРИРОВАНИЯ

Методические указания
к решению задач по теме «Методы интегрирования»
для студентов ФАВТ, ФМА, ФФиТРМ
дневного, вечернего и заочного отделений
САНКТ-ПЕТЕРБУРГ
2012
Составители: Н.И. Васильева, Е.Ю. Непомнящая
Рецензент: Е.Н. Бегун
Утверждено на заседании кафедры математики и информатики.
Протокол №8 от 9 января 2012 года.
Данные методические указания предназначены для самостоятельного изучения раздела высшей математики "Неопределенный интеграл" и содержат теоретические сведения и примеры решения задач по технике интегрирования.
Первообразная и неопределенный интеграл.
Определение 1. Функция  называется первообразной функции
называется первообразной функции 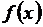 на интервале
на интервале 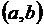 , если для любого
, если для любого  выполняется равенство
выполняется равенство
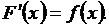
Пример.
Функция 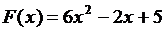 является первообразной для функции
является первообразной для функции 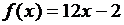 , так как
, так как  .
.
Функция 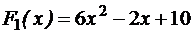 также является первообразной для функции
также является первообразной для функции 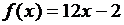 .
.
Мы видим, что две первообразные для одной и той же функции отличаются только постоянной.
Очевидно, что если  – первообразнаяи С – произвольная постоянная, то
– первообразнаяи С – произвольная постоянная, то 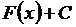 содержит все первообразные функции
содержит все первообразные функции 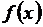 .
.
|
|
|
Определение 2. Совокупность всех первообразных 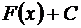 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  и обозначается символом
и обозначается символом 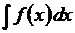 , то есть
, то есть

 ,
,
где 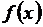 называется подынтегральной функцией,
называется подынтегральной функцией,  – подынтегральным выражением, а С – произвольной постоянной интегрирования.
– подынтегральным выражением, а С – произвольной постоянной интегрирования.
Примеры.
1.  , так как
, так как  .
.
2. 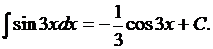
Понятно, что проверку нужно сделать дифференцированием. Сделайте это самостоятельно.
Свойства неопределенного интеграла.
1. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная от неопределенного интеграла равна подынтегральной функции:
 ,
,
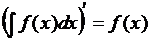 .
.
3. Постоянный множитель можно выносить за знак интеграла

4. Неопределенный интеграл от суммы двух или конечного числа функций равен сумме интегралов от этих функций:
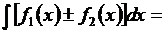
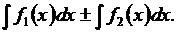
5. 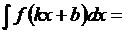
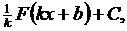
где  – первообразная функции
– первообразная функции 
Инвариантность формулы интегрирования
Если  , то и
, то и 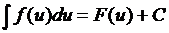 , где
, где  – произвольная функция, имеющая непрерывную производную.
– произвольная функция, имеющая непрерывную производную.
Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или функцией от нее.
|
|
|
Операция нахождения неопределенного интеграла называется интегрированием.
Запишем ряд интегралов, которые в дальнейшем будем считать табличными.
Таблица 1
1. 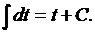
2. 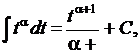 .
. 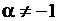
2а. 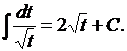
2b. 
3. 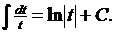
4. 
5. 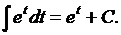
6. 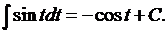
7. 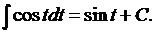
8. 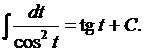
9. 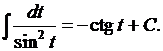
10.  .
.
11. 
12. 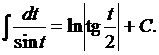
13. 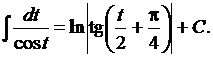
14. 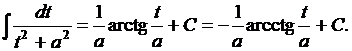
15. 
16. 
17. 
Формулы 2a и 2b являются частными случаями формулы 2 при  и
и 
В таблице аргумент подынтегральной функции обозначен через t, при этом аргумент может быть как независимой переменной, так и функцией.
В дальнейшем под термином "интеграл" мы будем понимать «неопределенный интеграл».
Вычисление интегралов с помощью таблицы интегралов и их свойств
Рассмотрим несколько интегралов, которые могут быть получены с использованием таблицы интегралов, свойств интегралов (§1) и преобразований подынтегральной функции.
1. Найти 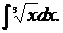
Решение.
Используя формулу 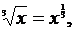 сведем интеграл к табличному (формула 2):
сведем интеграл к табличному (формула 2):


2. Найти 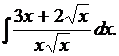
Решение.
Преобразуем подынтегральную функцию: проведем почленное деление и преобразование степеней.
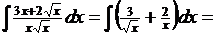
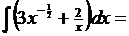



Здесь мы использовали свойства 3, 4, а также табличные интегралы 2,3.
3. Найти 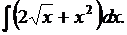
Решение.


4. Найти 
Решение.
Используя свойство 5 и табличный интеграл 5, получаем
|
|
|

5. Найти  .
.
Решение.
Для удобства вынесем знак минус за знак интеграла (свойство 3):
 .
.
Самостоятельно определите, какое свойство и какой табличный интеграл были использованы.
6. Найти 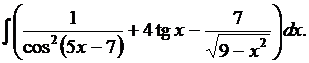
Решение.
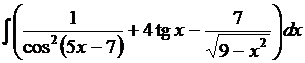

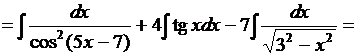

7. Найти 
Подынтегральную функцию преобразуем в сумму (см. Приложение).
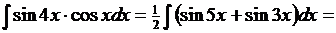
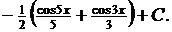
8. Найти 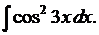
Преобразуем подынтегральную функцию, используя формулу понижения степени (см. Приложение) 

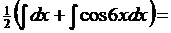

9. Найти 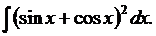
Преобразуем подынтегральную функцию.
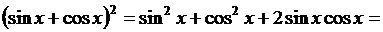
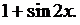


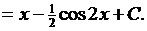
Задачи для самостоятельного решения.
Дата добавления: 2021-01-20; просмотров: 60; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
