Пример работы машины Тьюринга
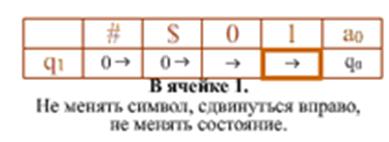
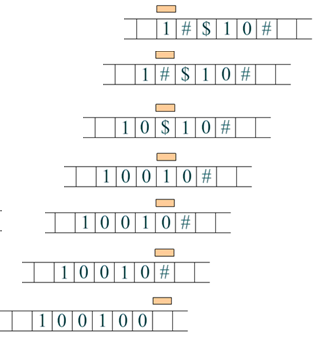
Допустим, на ленте есть слово, состоящее из символов #, $, 1 и 0. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над первой буквой слова слева. Завершается программа тогда, когда головка оказывается над пустым символом после самой правой буквы слова.
Примечание: длина слова и последовательность символов значения не имеют. На рисунке приводится пример последовательности выполнения команд для конкретного случая. Если на ленте будет другое слово, то и последовательность выполнения команд будет другой. Несмотря на это, данная программа для машины Тьюринга применима к любым словам описанного внешнего алфавита (соблюдается свойство применимости алгоритма ко всем однотипным задачам – массовость).
Можно усложнить программу. Допустим, головка располагается не обязательно над первым, а над любым символом слова. Тогда программа для данной машины Тьюринга может быть такой (а могла бы быть и другой):
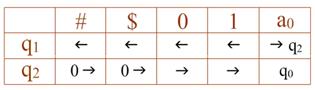
Задача. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над любой буквой слова.
Даны два целых положительных числа в десятичной системе счисления. Сконструировать машину Тьюринга, которая будет находить разность этих чисел, если известно, что первое число больше второго, а между ними стоит знак минус. Каретка находится над левой крайней цифрой левого числа.
Практическое применение результатов теории алгоритмов
Полученные в теории алгоритмов теоретические результаты находят достаточно широкое практическое применение, при этом можно выделить следующие два аспекта:
Теоретический аспект : при исследовании некоторой задачи результаты теории алгоритмов позволяют ответить на вопрос: является ли эта задача в принципе алгоритмически разрешимой. Для алгоритмически неразрешимых задач: возможно ли их сведение к задаче останова машины Тьюринга. В случае алгоритмической разрешимости задачи возникает следующий важный теоретический вопрос: о принадлежности этой задачи к классу NP–полных задач*. При утвердительном ответе на вопрос о принадлежности к классу NP–полных задач можно говорить о существенных временных затратах для получения точного решения для больших размерностей исходных данных.

Практический аспект : методы и методики теории алгоритмов позволяют осуществить:
· рациональный выбор из известного множества алгоритмов решения данной задачи с учетом особенностей их применения (например, при ограничениях на размерность исходных данных или объема дополнительной памяти);
· получение временных оценок решения сложных задач;
· получение достоверных оценок невозможности решения некоторой задачи за определенное время, что важно для криптографических методов;
· разработку и совершенствование эффективных алгоритмов решения задач в области обработки информации на основе практического анализа.
Понятие алгоритма
В сегодняшнем социуме слово «алгоритм» настолько широко распространено, что большинству интуитивно понятно. Под ним мы понимаем какую-либо последовательность шагов для достижения той или иной цели. Однако для теоретической науки понятие «алгоритма» достаточно сложное.
Считается, что однозначного определения алгоритма нет, хотя в основном различные источники дают очень близкие определения.
Итак, в широко распространенных определениях алгоритма можно выделить следующие составляющие:
Алгоритм – это конечная последовательность указаний …
· … на языке понятном исполнителю, …
· … задающая процесс решения задач определенного типа …
· … и ведущая к получению результата, однозначно определяемого допустимыми исходными данными.
В последнем пункте определения говорится о том, что результат выполнения алгоритма напрямую зависит от исходных данных. Т.е. один и тот же алгоритм при разных исходных данных даст разные результаты. С другой стороны, если одному и тому же алгоритму передать несколько раз одни и те же данные, он должен столько же раз выдать один и тот же результат.
Свойства алгоритма
· Дискретность (в данном случае, разделенность на части) и упорядоченность. Алгоритм должен состоять из отдельных действий, которые выполняются последовательно друг за другом.
· Детерминированность (однозначная определенность). Многократное применение одного алгоритма к одному и тому же набору исходных данных всегда дает один и тот же результат.
· Формальность. Алгоритм не должен допускать неоднозначности толкования действий для исполнителя.
· Результативность и конечность. Работа алгоритма должна завершаться за определенное число шагов, при этом задача должна быть решена.
· Массовость. Определенный алгоритм должен быть применим ко всем однотипным задачам.
Дата добавления: 2020-12-12; просмотров: 497; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
