Цели и задачи теории алгоритмов
Лекция 8. А лгоритмизация и программирование
Введение в теорию алгоритмов
Исторический обзор
Первым дошедшим до нас алгоритмом в его интуитивном понимании – конечной последовательности элементарных действий, решающих поставленную задачу, считается предложенный Евклидом в III веке до нашей эры алгоритм нахождения наибольшего общего делителя двух чисел (алгоритм Евклида).
Отметим, что в течение длительного времени, вплоть до начала XX века само слово «алгоритм» употреблялось в устойчивом сочетании «алгоритм Евклида». Для описания пошагового решения других математических задач использовалось слово «метод».
 Слово «алгоритм» происходит от имени ученого IX века Муххамеда бен Аль-Хорезми («аль-хорезми» - «алгоритм»), который описал правила выполнения арифметических действий в десятичной системе счисления.
Слово «алгоритм» происходит от имени ученого IX века Муххамеда бен Аль-Хорезми («аль-хорезми» - «алгоритм»), который описал правила выполнения арифметических действий в десятичной системе счисления.

Сначала определение понятия алгоритма было проблемой математики, однако с течением времени теория алгоритмов стала развиваться за счет влияния открытий не только в математике, но и в информатике. В настоящее время алгоритм является одним из главных понятий информатики.
Другими словами, следует понимать, что первоначально теория алгоритмов возникла в математике и представляла собой поиск способов решения задач определенного типа посредством определенного набора указаний.
Теория алгоритмов
Теория алгоритмов - раздел математики, в котором изучаются теоретические возможности эффективных процедур вычисления (алгоритмов) и их приложения. Теория алгоритмов является в настоящее время важным и быстроразвивающимся разделом математической логики. Интерес к ней объясняется, с одной стороны, внутренними интересами самой математики (алгоритмические проблемы алгебры, вопросы оснований математики и т.п.), а, с другой - бурным развитием электронной вычислительной техники и теоретической кибернетики. Практические и теоретические вопросы реализации алгоритмов на современных вычислительных машинах являются содержанием такого важного раздела теоретической кибернетики, как программирование.
|
|
|
Точные математические понятия, которые в том или ином смысле формализовали интуитивное понятие алгоритма, предложены только в середине 30-х годов нашего столетия. Исторически первые из предложенных понятий можно разделить на два вида.
1. Описывается некоторый класс арифметических функций (вообще говоря, частных), то есть функций от конечного числа натуральных аргументов с натуральными значениями. Эти функции обладают некоторыми эффективными процедурами нахождения значения функции (если оно существует) по заданным значениям аргументов. Функции из этого класса называются частично рекурсивными (ч.р.ф.), а в случае, если ч.р.ф. всюду определены, их называют общерекурсивными.
|
|
|
2. Описываются точные математические понятия машины и вычислимости на машине. Такие понятия машины и вычислимости на машине предложили независимо один от другого Э.Пост и А.Тьюринг. Эти "теоретические вычислительные машины" обычно называют машинами Тьюринга. Оказалось, что класс арифметических функций, для которых существует машина Тьюринга, вычисляющая по значениям аргументов значение функции (если оно существует), совпадает с классом всех ч.р.ф. и наоборот, каждая ч.р.ф. вычислима на подходящей машине Тьюринга.
В общих чертах различие между двумя рассмотренными выше видами определений можно сформулировать так: в первом дается точное описание класса вычислимых арифметических функций, во втором - точное описание некоторого класса алгоритмических преобразований (вычислений на машине Тьюринга).
Начальной точкой отсчета современной теории алгоритмов можно считать работу немецкого математика Курта Гёделя (1931 год - теорема о неполноте символических логик), в которой было показано, что некоторые математические проблемы не могут быть решены алгоритмами из некоторого класса. Общность результата Геделя связана с тем, совпадает ли использованный им класс алгоритмов с классом всех (в интуитивном смысле) алгоритмов. Эта работа дала толчок к поиску и анализу различных формализаций алгоритма.
|
|
|
Первые фундаментальные работы по теории алгоритмов были опубликованы независимо в 1936 году годы Аланом Тьюрингом, Алоизом Черчем и Эмилем Постом. Предложенные ими машина Тьюринга, машина Поста и лямбда-исчисление Черча были эквивалентными формализмами алгоритма. Сформулированные ими тезисы (Поста и Черча-Тьюринга) постулировали эквивалентность предложенных ими формальных систем и интуитивного понятия алгоритма. Важным развитием этих работ стала формулировка и доказательство алгоритмически неразрешимых проблем.
В 1950-е годы существенный вклад в теорию алгоритмов внесли работы Колмогорова и Маркова.
Колмогоров: Алгоритм – это всякая система вычислений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.
Марков: Алгоритм – это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату.
|
|
|
К 1960-70-ым годам оформились следующие направления в теории алгоритмов:
· Классическая теория алгоритмов (формулировка задач в терминах формальных языков, понятие задачи разрешения, введение сложностных классов, формулировка в 1965 году Эдмондсом проблемы P=NP, открытие класса NP-полных задач и его исследование);
· Теория асимптотического анализа алгоритмов (понятие сложности и трудоёмкости алгоритма, критерии оценки алгоритмов, методы получения асимптотических оценок, в частности для рекурсивных алгоритмов, асимптотический анализ трудоемкости или времени выполнения), в развитие которой внесли существенный вклад Кнут, Ахо, Хопкрофт, Ульман, Карп;
· Теория практического анализа вычислительных алгоритмов (получение явных функции трудоёмкости, интервальный анализ функций, практические критерии качества алгоритмов, методика выбора рациональных алгоритмов), основополагающей работой в этом направлении, очевидно, следует считать фундаментальный труд Д. Кнута «Искусство программирования для ЭВМ».
Отметим, что различные определения алгоритма, в явной или неявной форме, постулируют следующий ряд требований:
ü алгоритм должен содержать конечноеколичество элементарно выполнимых предписаний, т.е. удовлетворять требованию конечности записи;
ü алгоритм должен выполнять конечное количество шагов при решении задачи, т.е. удовлетворять требованию конечности действий;
ü алгоритм должен быть единым для всех допустимых исходных данных, т.е. удовлетворять требованию универсальности;
ü алгоритм должен приводить к правильному по отношению к поставленной задаче решению, т.е. удовлетворять требованию правильности.
Другие формальные определения понятия алгоритма связаны с введением специальных математических конструкций (машина Поста, машина Тьюринга, рекурсивно-вычислимые функции Черча) и постулированием тезиса об эквивалентности такого формализма и понятия «алгоритм».
Цели и задачи теории алгоритмов
Обобщая результаты различных разделов теории алгоритмов можно выделить следующие цели и соотнесенные с ними задачи, решаемые в теории алгоритмов:
· формализация понятия «алгоритм» и исследование формальных алгоритмических систем;
· формальное доказательство алгоритмической неразрешимости ряда задач;*
· классификация задач, определение и исследование сложностных классов;
· асимптотический анализ сложности алгоритмов;
· исследование и анализ рекурсивных алгоритмов;
· получение явных функций трудоемкости в целях сравнительного анализа алгоритмов;
· разработка критериев сравнительной оценки качества алгоритмов.

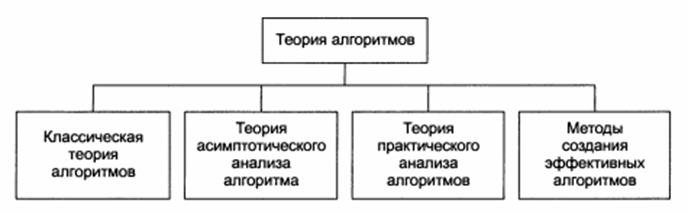
Разделы современной теории алгоритмов
Рассмотрим одну из фундаментальных работ по теории алгоритмов.
Строгие определения понятия «алгоритм» связаны с введением специальных математических конструкций – формальных моделей вычислений. Одной из таких моделей является машина Тьюринга.
В 1936 г. Аланом Тьюрингом для уточнения понятия алгоритма был предложен абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель. Например, операции, которые выполняют реальные вычислительные машины можно имитировать на универсальном исполнителе. В последствие, придуманная Тьюрингом вычислительная конструкция была названа машиной Тьюринга.
Кроме того, предполагается, что универсальный исполнитель должен уметь доказывать существование или отсутствие алгоритма для той или иной задачи.
Машина Тьюринга состоит из бесконечной в обе стороны ленты, разделенной на ячейки. Лента может протягиваться на одну клетку вправо или влево под управлением автомата (головки), которая является неподвижной.
Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице.
Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:
· Внешний алфавит. Конечное множество (например, А), элементы которого называются буквами (символами). Одна из букв этого алфавита (например, а0) должна представлять собой пустой символ.
· Внутренний алфавит. Конечное множество состояний головки (автомата). Одно из состояний (например, q1) должно быть начальным (запускающим программу). Еще одно из состояний (q0) должно быть конечным (завершающим программу) – состояние останова.
· Таблица переходов. Описание поведения автомата (головки) в зависимости от состояния и считанного символа.
Автомат машины Тьюринга в процессе своей работы может выполнять следующие действия:
· Записывать символ внешнего алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой).
· Передвигаться на одну ячейку влево или вправо.
· Менять свое внутреннее состояние.
Одна команда для машины Тьюринга как раз и представляет собой конкретную комбинацию этих трех составляющих: указаний, какой символ записать в ячейку (над которой стоит автомат), куда передвинуться и в какое состояние перейти. Хотя команда может содержать и не все составляющие (например, не менять символ, не передвигаться или не менять внутреннего состояния).
Дата добавления: 2020-12-12; просмотров: 125; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
