Интегрирование определенного интеграла методом подстановки
Пусть для вычисления интеграла  от непрерывной функции сделана подстановка х=φ(t). Если функция х=φ(t) и её производная
от непрерывной функции сделана подстановка х=φ(t). Если функция х=φ(t) и её производная 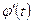 непрерывны на отрезке [α, β], причём a=φ(α), b=φ(β), то справедлива формула:
непрерывны на отрезке [α, β], причём a=φ(α), b=φ(β), то справедлива формула:
 . .
|
Отметим, что :
1).функцию х=φ(t) следует подобрать так, чтобы, подставив её вместо х в подынтегральное выражение, получить более простой интеграл;
2).при вычислении определённого интеграла методом подстановки возвращаться к старой переменной не требуется;
3) вместо подстановки х=φ(t) применяют и подстановку t=ψ(x).
Пример 7.
С помощью подстановки вычислить интегралы:
а)  ; б)
; б)  ; в)
; в)  .
.
Решение.
а). Применим подстановку  . Тогда x=t2; dx=2tdt.
. Тогда x=t2; dx=2tdt.
Находим новые пределы интегрирования:
| x | 1 | 9 |
| t=√x | 1 | 3 |
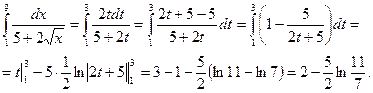
б). Положим  . Тогда получаем x= 2arctgt, dx=
. Тогда получаем x= 2arctgt, dx= 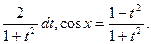
Находим новые пределы интегрирования:
| x | 0 | 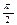
|
| t | 0 | 1 |
 в). Полагая t=3-x, получим : x=3-t, dx=-dt. Пределы интегрирования:
в). Полагая t=3-x, получим : x=3-t, dx=-dt. Пределы интегрирования:
| x | 2 | 3 |
| t | 1 | 0 |

Интегрирование определенного интеграла по частям
Если функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [a;b], то имеет место формула

|
Пример 8.
Вычислить интегралы с помощью формулы интегрирования по частям:
а)  ; б)
; б)  ; в)
; в) 
Решение.
а). Пусть u=lnx, dv=(x+1)dx. Тогда 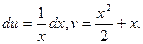

б). Пусть u=arctgx, dv=dx. Тогда  Имеем
Имеем

в). Пусть u=x2, dv=sin2xdx, du=2xdx, v=-1/2cos2x.
 Снова интегрируем по частям: u=x, dv=cos2xdx, du=dx, v=1/2sin2x.
Снова интегрируем по частям: u=x, dv=cos2xdx, du=dx, v=1/2sin2x.
|
|
|


Приложения определённого интеграла
Вычисление площадей плоских фигур
Площадь криволинейной трапеции, ограниченной сверху графиком функции y=f(x) (f(x)≥0), слева и справа соответственно прямыми х=а и х=b, снизу отрезком [a;b] оси Ох, вычисляется по формуле

|

В этом и состоит геометрический смысл определённого интеграла: он численно равен площади криволинейной трапеции.
Если f(x)≤0 при хє[a;b], то
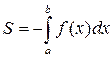
|
Площадь фигуры, ограниченной кривыми y=f1(x) и y=f2(x), причём f1(x)≤f2(x), прямыми х=а и х=b вычисляется по формуле

|
Пример 9.
Вычислить площадь между кривыми y1=x2 и y2=3x.
Решение.
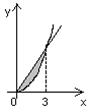
Найдём абсциссу точки пересечения графиков данных функций, для этого решаем уравнение: x2=3x.
Отсюда х1=0, х2=3.

Ответ: 4,5 кв.ед.
Вычисление объёмов тел
Если криволинейная трапеция, ограниченная кривой y=f(x) и прямыми y=0, x=a, x=b, вращается вокруг оси 0x, то объём тела вращения вычисляется по формуле:
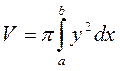
|
Пример 10.
Найти объём тела, образуемого вращением вокруг оси 0х сегмента параболы y=x2-4.
Решение.
Найдём точки пересечения параболы y=x2-4 с осью 0х:
x2-4=0; х1=-2, х2=2;
 парабола пересекает ось 0х в точках А(-2;0) и В(2;0), построим её.
парабола пересекает ось 0х в точках А(-2;0) и В(2;0), построим её.
 Ответ: V=
Ответ: V= 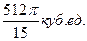
Пример 11.
|
|
|
Найти объём тела, образованного вращением вокруг оси 0х
фигуры, ограниченной кривой y2=(x-1)3 и прямой х=2.
Решение.

 Ответ: V=
Ответ: V=  куб.ед.
куб.ед.
Дата добавления: 2020-11-29; просмотров: 99; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
