Основные способы интегрирования

1.Метод непосредственного интегрирования

 заключается в использовании основных свойств неопределённого интеграла и приведении подынтегрального выражения к табличному виду.

 Пример 2.

Используя таблицу и основные свойства неопределённого интеграла, найти интеграл:

а) 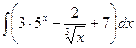; б)

Решение.

б) Почленно поделим числитель подынтегральной дроби на знаменатель: 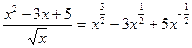. Отсюда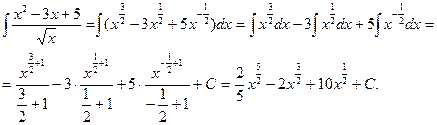

2. Метод подстановки (замена переменной)

Замена переменной в неопределённом интеграле производится с помощью подстановок двух видов:

1). х=φ(t), где φ(t) – монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид

Из формулы следует, что для вычисления интеграла  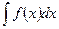с помощью подстановки x=φ(t) надо в функции f(x) заменить х через φ(t) и положить

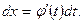
2). u=ψ(x), где u – новая переменная. Формула замены переменной в этом случае имеет вид

 

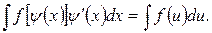
Полученные после применения той или иной подстановки интегралы должны быть более удобны для интегрирования, чем исходные.

 

 

Пример 3.

Найти интеграл, используя подходящую подстановку:

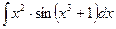а)  ; б) ; в) .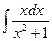

Решение.

а) Применим подстановку t=7x-1. Тогда dt=7dx, откуда dx=1/7dt. Поэтому

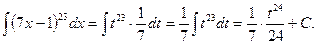
Возвращаясь к переменной х, получим окончательно:

б) Подынтегральное выражение содержит сложную функцию sin(x³+1), поэтому стоит попробовать подстановку t= x³+1. Тогда dt=d(x³+1)=3x²dx, откуда x²dx=1/3dt. Таким образом,

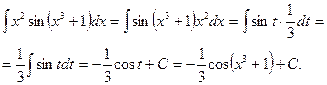
в) Сделаем замену t=x²+1, тогда , .

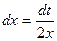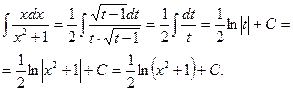
Мы избавились от знака модуля в последнем выражении, так как х²+1>0, для любых х.

 

Пример 4.

Найти интеграл, используя подходящую подстановку х=φ(t):

а) 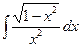; б) .

Решение.

а) Сделаем такую замену х=φ(t), чтобы подкоренное выражение 1-х² стало полным квадратом. Например x=sint. Тогда dx=costdt:

Учитывая, что t=arcsin x, получим окончательно:

б) Сделаем замену x=t², чтобы корни извлекались нацело, тогда dx=2tdt, t=√x :

Понятие об определенном интеграле

Теорема Ньютона–Лейбница

Теорема Ньютона – Лейбница.

Пусть f – данная функция, F – её произвольная первообразная. Тогда

Определённый интеграл – это разность значений любой первообразной функции для f)x) при верхнем и нижнем пределах интегрирования.

Алгоритм нахождения определённого интеграла .

I. Найти первообразную функцию F(x) для функции f(x).

II.Вычислить значение F(x) при х=b ( b – верхний предел).

III.Вычислить значение F(x) при х=а ( а – нижний предел).

IV.Вычислить разность .

Пример 5.

Вычислить определённые интегралы:

а) ; б) ; в) .

Решение.

а)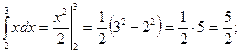

б) ;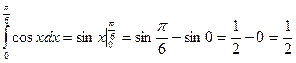

Основные свойства определённого интеграла

1.При перестановке пределов изменяется знак интеграла:

.

2.Интеграл с одинаковыми пределами равен нулю:

.

3.Переменную интегрирования можно обозначать любой буквой:

.

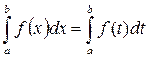4.Определённый интеграл суммы функций равен сумме определённых интегралов этих функций:

.

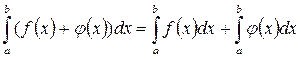5.Постоянный множитель подынтегрального выражения можно выносить за знак определённого интеграла:

.

Пример 6.

Используя свойства определённого интеграла, вычислить интегралы:

а) ; б) .

Решение.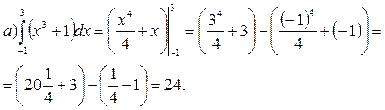

---

Дата добавления: 2020-11-29; просмотров: 101; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!