Как находить нули числителя и знаменателя?

Метод интервалов, примеры, решения.

Метод интервалов (или как его еще иногда называют метод промежутков) – это универсальный метод решения неравенств. Он подходит для решения разнообразных неравенств, однако наиболее удобен в решении рациональных неравенств с одной переменной. Поэтому в школьном курсе алгебры метод интервалов вплотную привязывают именно к рациональным неравенствам, а решению других неравенств с его помощью практически не уделяют внимания.

В этой статье мы детально разберем метод интервалов и затронем все тонкости решения неравенств с одной переменной с его помощью. Начнем с того, что приведем алгоритм решения неравенств методом интервалов. Дальше поясним, на каких теоретических аспектах он базируется, и разберем шаги алгоритма, в частности, подробно остановимся на определении знаков на интервалах. После этого перейдем к практике и покажем решения нескольких типовых примеров. А в заключение рассмотрим метод интервалов в общем виде (то есть, без привязки к рациональным неравенствам), другими словами, обобщенный метод интервалов.

Алгоритм

Знакомство с методом интервалов в школе начинается при решении неравенств вида f(x)<0 (знак неравенства может быть и другим ≤, > или ≥), где f(x) – это либо многочлен, представленный в виде произведения линейных двучленов с коэффициентом 1 при переменной x и/или квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом и их степеней, либо отношение таких многочленов. Для наглядности приведем примеры подобных неравенств: (x−5)·(x+5)≤0, (x+3)·(x²−x+1)·(x+2)³≥0, , .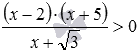

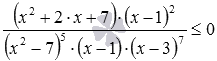Чтобы сделать дальнейший разговор предметным, сразу запишем алгоритм решения неравенств указанного выше вида методом интервалов, а потом разберемся, что да как да почему. Итак, по методу интервалов:

· Сначала находятся нули числителя и нули знаменателя. Для этого числитель и знаменатель выражения в левой части неравенства приравниваются к нулю, и решаются полученные уравнения.

· После этого точки, соответствующие найденным нулям, отмечаются черточками на координатной прямой. Достаточно схематического чертежа, на котором не обязательно соблюдать масштаб, главное придерживаться расположения точек относительно друг друга: точка с меньшей координатой находится левее точки с большей координатой. После этого выясняется, какими следует их изобразить: обычными или выколотыми (с пустым центром). При решении строгого неравенства (со знаком < или >) все точки изображаются выколотыми. При решении нестрогого неравенства (со знаком ≤ или ≥) точки, отвечающие нулям знаменателя, делаются выколотыми, а оставшиеся отмеченные черточками точки – обычными. Эти точки разбивают координатную прямую на несколько числовых промежутков.

· Дальше определяются знаки выражения f(x) из левой части решаемого неравенства на каждом промежутке (как это делается, подробно расскажем в одном из следующих пунктов), и над ними проставляются + или − в соответствии с определенными на них знаками.

· Наконец, при решении неравенства со знаком < или ≤ изображается штриховка над промежутками, отмеченными знаком −, а при решении неравенства со знаком > или ≥ - над промежутками, отмеченными знаком +. В результате получается геометрическое представление числового множества, которое и является искомым решением неравенства.

Заметим, что приведенный алгоритм согласован с описанием метода интервалов в школьных учебниках [1, с. 12-23; 2, с. 88-91].

На чем базируется метод?

Подход, лежащий в основе метода интервалов, имеет место в силу следующего свойства непрерывной функции [3, с. 125]: если на интервале (a, b) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак (от себя добавим, что аналогичное свойство справедливо и для числовых лучей (−∞, a) и (a, +∞)). А это свойство в свою очередь следует из теоремы Больцано-Коши (ее рассмотрение выходит за рамки школьной программы), формулировку и доказательство которой при необходимости можно найти, например, в книге [4, с. 123-124].

Для выражений f(x), имеющих указанный в предыдущем пункте вид, постоянство знака на промежутках можно обосновать и иначе, отталкиваясь от свойств числовых неравенств и учитывая правила умножения и деления чисел с одинаковыми знаками и разными знаками.

В качестве примера рассмотрим неравенство 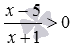. Нули его числителя и знаменателя разбивают числовую прямую на три промежутка (−∞, −1), (−1, 5) и (5, +∞). Покажем, что на промежутке (−∞, −1) выражение из левой части неравенства имеет постоянный знак (можно взять и другой промежуток, рассуждения будут аналогичными). Возьмем любое число t из этого промежутка. Оно, очевидно, будет удовлетворять неравенству t<−1, и так как −1<5, то по свойству транзитивности, оно же будет удовлетворять и неравенству t<5. Из этих неравенств в силу свойств числовых неравенств следует, что t+1<0 и t−5<0. То есть, t+1 и t−5 – отрицательные числа, не зависимо от того, какое конкретно число t мы возьмем из промежутка (−∞, −1). Тогда правило деления отрицательных чисел позволяет констатировать, что значение выражения будет положительным, откуда следует, что значение выражения будет положительным при любом значении x из промежутка (−∞, −1). Итак, на указанном промежутке выражение имеет постоянный знак, причем, это знак +.

Так мы плавно подошли к вопросу определения знаков на промежутках, но не будем перескакивать через первый шаг метода интервалов, подразумевающий нахождение нулей числителя и знаменателя.

Как находить нули числителя и знаменателя?

С нахождением нулей числителя и знаменателя дроби указанного в первом пункте вида обычно не возникает никаких проблем. Для этого выражения из числителя и знаменателя приравниваются к нулю, и решаются полученные уравнения. Принцип решения уравнений такого вида подробно изложен в статье решение уравнений методом разложения на множители. Здесь лишь ограничимся примером.

Рассмотрим дробь 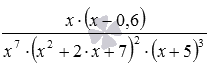и найдем нули ее числителя и знаменателя. Начнем с нулей числителя. Приравниваем числитель к нулю, получаем уравнение x·(x−0,6)=0, от которого переходим к совокупности двух уравнений x=0 и x−0,6=0, откуда находим два корня 0 и 0,6. Это искомые нули числителя. Теперь находим нули знаменателя. Составляем уравнение x⁷·(x²+2·x+7)²·(x+5)³=0, оно равносильно совокупности трех уравнений x⁷=0, (x²+2·x+7)²=0, (x+5)³=0, и дальше x=0, x²+2·x+7=0, x+5=0. Корень первого из этих уравнений очевиден, это 0, второе уравнение корней не имеет, так как его дискриминант отрицательный, а корень третьего уравнения есть −5. Итак, мы нашли нули знаменателя, их оказалось два: 0 и −5. Заметим, что 0 оказался как нулем числителя, так и нулем знаменателя.

Для нахождения нулей числителя и знаменателя в общем случае, когда в левой части неравенства дробь, но не обязательно рациональная, также числитель и знаменатель приравниваются к нулю, и решаются соответствующие уравнения.

Дата добавления: 2020-11-27; просмотров: 480; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!