Методы вычисления определителей.
1. Разложение по строке или столбцу.
2. Метод обращения в нуль всех (кроме одного) элементов строки или столбца. Метод состоит в том, что с учетом свойств определителя при помощи какого-либо столбца (строки) путём умножения его на соответствующие числа и вычитания из остальных столбцов (строк), зануляются все элементы выбранной строки (столбца) кроме одного, принадлежащего вычитаемому столбцу (строке).
3. Метод приведения к треугольному виду. Алгоритм, предложенный в предыдущем пункте, используется для последовательного зануления всех элементов первой строки (столбца) кроме одного, второй строки (столбца) – всех кроме двух и т.д. В итоге определитель преобразуется к треугольному виду. Величина такого определителя равна произведению элементов главной диагонали.
4. Вычисление с использованием теоремы Лапласа, согласно которой определитель 
- го порядка равен сумме произведений всех его миноров 
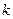- го порядка, стоящих в выделенных 
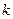строках (столбцах), на их алгебраические дополнения.
Примеры.
1. Вычислить данный определитель четвёртого порядка с помощью разложения по строке или столбцу:
Решение. Удобнее всего делать разложение по строке или столбцу, в которых встречается наибольшее число нулевых элементов. В данном случае – это четвёртый столбец. Итак, имеем
 |
Полученные в итоге два определителя третьего порядка вычислим тем же методом. В определителе 
нулевых элементов нет, поэтому можно выбрать для разложения любой из столбцов, например, первый. В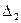 
единственный нулевой элемент находится на пересечении первого столбца со второй строкой. Для разнообразия будем разлагать 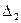по второй строке:
|
|
|
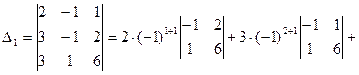
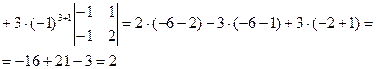
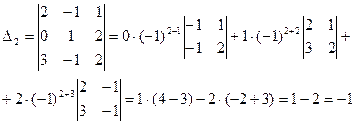
Таким образом, окончательно получим 
.
Система линейных алгебраических уравнений. Основная и расширенная матрица. Совместная, несовместная и однородная системы уравнений.
Система линейных алгебраических уравнений, содержащая 
уравнений и неизвестных имеет следующий вид:
(1)
Обозначим матрицу-столбец из неизвестных через X и матрицу-столбец из свободных членов через B.
– столбец неизвестных, 
– столбец свободных членов.
Тогда систему (1) можно записать в виде: 
, (2)
где 
– основная матрица системы.
Уравнение (2) называется матричным уравнением. Перепишем уравнение (2) следующим образом 
.
Тогда получим решение матричного уравнения в виде: 
(3)
Матрицу 
называют расширенной матрицей системы.
Определение. Система линейных алгебраических уравнений называется прямоугольной, если 
, и квадратной, если 
.
Определение. Система линейных алгебраических уравнений называется однородной, если 
, т.е., если столбец свободных членов состоит из одних нулей.
|
|
|
Определение. Система линейных алгебраических уравнений называется неоднородной, если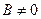 
.
Определение. Система линейных алгебраических уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Определение. Совместная система линейных алгебраических уравнений называется определенной, если она имеет только одно решение, и неопределенной, если она имеет более одного решения.
Определение. Две системы называются эквивалентными, если любое решение одной из них является решением и другой системы. Заметим, что все несовместные системы являются эквивалентными.
Элементарные преобразования системы линейных уравнений:
1. перестановка любых двух уравнений;
2. умножение обеих частей одного уравнения на любое число отличное от нуля;
3. прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число.
Элементарные преобразования переводят данную систему в эквивалентную.
Дата добавления: 2020-11-15; просмотров: 99; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!