Прием моделирования с помощью диаграмм (кругов) Эйлера-Венна
Данный метод позволяет графически решать математические задачи на основе применения теории множеств.
Задача 10. В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический – 14, химический – 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек – и математический и физический, 5 – и математический и химический, 3 – и физический и химический.
Сколько учеников класса не посещают никаких кружков?
Решение.
На рисунке самый большой круг изображает множество всех учеников класса. Внутри этого круга расположены три пересекающихся круга меньшего диаметра: эти круги изображают членов математического, физического и химического кружков и обозначены буквами М, Ф, Х.
Пусть МФХ – множество ребят, каждый из которых посещает все 3 кружка. Дадим аналогичные имена и другим множествам: МФ – множество занимающихся и в математическом, и в физическом кружке (и, возможно, также в химическом), МФ - и в математическом, и в физическом, но не в химическом и т.д.
Впишем нужные имена множеств в области, изображенные на рисунке:
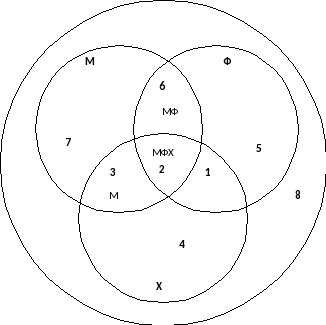
Х
Обратимся к числовым данным. В область МФХ впишем число 2, так как все три кружка посещают 2 ученика. Далее известно, что ребят, посещающих и математический, и физический кружок, - 8. Значит, множество МФ состоит из 8 человек. Но это множество является объединением множеств МФХ и МФ, причем в МФХ входят 2 человека. Значит, на долю МФ остается 6 человек.
|
|
|
Теперь рассмотрим множество МХ, состоящее из 5 человек. Оно также состоит из двух частей: на МФХ приходится 2 человека. Значит, на МХ – 3.
Множество ФХ состоит из 3 человек. На ФХ приходится 1 человек.
Рассмотрим теперь множество М, в которое входит 18 учеников. Оно состоит из четырех частей. Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 3. Значит, в четвертое подмножество, а именно в М, входит 18 – (2 + 3 + 6) = 7 человек.
Аналогично определим количество учащихся в множествах и :
14 – (6 + 2 + 1) = 5, 10 – (3 + 2 + 1) = 4.
Три пересекающихся круга образуют 7 непересекающихся областей, изображающих непересекающиеся подмножества учеников, каждый из которых посещает хотя бы 1 кружок. Просуммируем цифры в этих областях: 6 + 5 + 7 + 3 + 2 + 1 + 4 = 28 человек посещает кружки.
Значит, 36 – 28 = 8 ребят не посещают никаких кружков.
Ответ: в классе 8 учеников, не посещающих кружки.
Задача 11. Среди 150 школьников марки собирают только мальчики. 67 человек собирают марки СССР, 48 человек – Африки и 32 человека – Америки, 11 человек – только СССР, 7 человек – только Африки, 4 человека – только Америки и только Иванов собирал марки СССР, Африки, Америки. Найдите максимальное число девочек.
|
|
|
Решение.
Изобразим с помощью кругов Эйлера условие задачи
Имеем систему трех уравнений:
(56 = 67 – 11),
(41 = 48 – 7),
(28 = 32 – 4),
откуда 2 (x + y + z) = 122, т.е. x + y + z = 61.
Следовательно, марки собирают 61 + 11 + 7 + 4 + 1 = 84 мальчика, максимальное число девочек: 150 – 84 = 66.
Ответ: 66 девочек.
Задача 12. После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников класса двое не были ни в кино, ни в театре, ни в цирке. В кино побывало 25 человек, в театре – 11, в цирке – 17; и в кино, и в театре – 6; и в кино, и в цирке – 10; и в театре, и в цирке – 4.
Сколько человек побывало и в кино, и в театре, и в цирке?
Решение.
Изобразим с помощью кругов Эйлера условие задачи.
В область КТЦ впишем х. Известно, что в кино и в театре побывала 6 человек, значит, на долю КТ остается (6 –х) человек. Аналогично на КЦ приходится (10 – х) человек, на ТЦ – (4 – х) человек.
Рассмотрим множество К, в которое входит 25 человек. Оно состоит из четырех частей. Количественный состав трех подмножеств мы уже нашли: это х, 6-х и 10-х. Значит, в четвертое подмножество, содержащее ребят, которые побывали только в кино входит
|
|
|
25 – (х + 6 – х + 10 – х) = 9 + х человек.
Аналогично определим количество учащихся, посетивших только театр:
11 – (х + 6 – х + 4 – х) = 1 + х и количество учащихся, посетивших только цирк:
17 – (х + 10 – х + 4 – х) = 3 + х.
Просуммируем выражения в 7 непересекающихся областях, изображающих подмножества учеников, каждый из которых посетил хотя бы одно культурное заведение:
(9+х)+(6-х)+(1+х)+(10-х)+х+(4-х)+(3+х)=33+х.
По условию из 36 учеников класса 2 ученика нигде не были. Значит,
33 + х = 34, х = 1
Ответ: один человек побывал и в кино, и в театре, и в цирке.
Дата добавления: 2020-11-15; просмотров: 98; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
