Задача линейного программирования в канонической форме
ПРИМЕР № 1: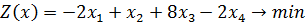 
Алгоритм решения задачи методом искусственного базиса:
1) В рассматриваемом примере исходная задача приведена в канонической форме и не имеет начального базиса, следовательно, нужно ввести искусственный базис, который войдёт в целевую функцию с коэффициентами «+М», т.к. задача решается на отыскание минимума (рис. 5.1.1):
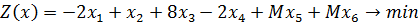
Рисунок 5.1.1. Введение искусственного базиса
2) Составляем симплексную таблицу. В столбец «Базис» вписываем базисные векторы из системы ограничений и заполняем таблицу коэффициентами векторов из системы ограничений (табл. 5.1.1):
Таблица 5.1.1
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 |
| х5 | 6 | 5 | –1 | –7 | 2 | 1 | 0 |
| х6 | 2 | 3 | –1 | –4 | 1 | 0 | 1 |
3) Ввиду того, что начальное опорное решение расширенной задачи содержит искусственные переменные, входящие в целевую функцию с коэффициентом «+М» вычисляемые оценки разложений векторов системы ограничений по базису, которые являются признаками оптимальности решения,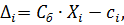 
состоят из двух слагаемых: 
одно из которых ( 
) не зависит от М, а другое (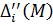 
) зависит от М.
Для разбираемой в данном примере задачи оценки разложений векторов будут следующими:
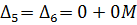
Далее вносим вычисленные оценки в симплексную таблицу (табл. 5.1.2):
Таблица 5.1.2
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | ||
| х5 | 6 | 5 | –1 | –7 | 2 | 1 | 0 | ||
| х6 | 2 | 3 | –1 | –4 | 1 | 0 | 1 | ||
| Δ ’ | 0 | 2
| –1 | –8 | 2 | 0 | 0 | ||
| Δ ’’ | 8M | 8M | –2M | –11M | 3M | 0 | 0 |
4) В данном примере задача решается на минимум, поэтому помечаем положительные оценки векторов в строке Δ’’ (табл. 5.1.2):
5) Для найденных оценок вычисляем вспомогательный параметр 
для оценки векторов х1 и х2 (табл. 5.1.3):
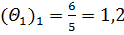
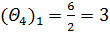
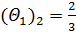
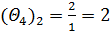
Таблица 5.1.3
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ4 |
| х5 | 6 | 5 | –1 | –7 | 2 | 1 | 0 | 1,2 | 3 |
| х6 | 2 | 3 | –1 | –4 | 1 | 0 | 1 | 2/3 | 2 |
| Δ ’ | 0 | 2 | –1 | –8 | 2 | 0 | 0 | ||
| Δ ’’ | 8M | 8M | –2M | –11M | 3M | 0 | 0 |
6) Выбираем минимальный параметр 
в каждом столбце и составляем критерий выбора вектора, вводимого в базис:
.
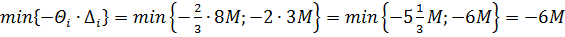Cледовательно, новым базисным вектором будет 
, и он заменит собой вектор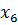 
(табл. 5.1.3):
7) Далее применяем элементарные преобразования Жордана-Гаусса и приводим выбранный столбец ( ) к базисному виду. При этом разрешающий элемент находится на пересечении выбранного столбца и выбранной строки (в нашем примере он равен 1, табл. 5.1.3). В М-методе векторы, соответствующие искусственным переменным, которые выводятся из базиса, исключаются из рассмотрения и далее не рассчитываются. Проведённые расчёты представлены в табл. 5.1.4 (вспомогательный параметр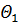 
в расчётах не участвует):
|
|
|
Таблица 5.1.4
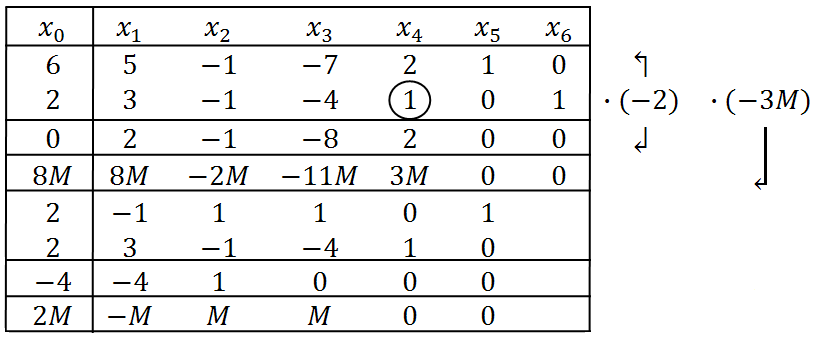
8) После выполнения преобразований симплексная таблица будет выглядеть следующим образом (табл. 5.1.5).
Таблица 5.1.5
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ4 |
| х5 | 6 | 5 | –1 | –7 | 2 | 1 | 0 | 1,2 | 3 |
| х6 | 2 | 3 | –1 | –4 | 1 | 0 | 1 | 2/3 | 2 |
| Δ ’ | 0 | 2 | –1 | –8 | 2 | 0 | 0 | ||
| Δ ’’ | 8M | 8M | –2M | –11M | 3M | 0 | 0 | Θ2 | Θ3 |
| х5 | 2 | –1 | 1 | 1 | 0 | 1 | 2 | 2 | |
| х4 | 2 | 3 | –1 | –4 | 1 | 0 | – | – | |
| Δ ’ | –4 | –4 | 1 | 0 | 0 | 0 | |||
| Δ ’’ | 2М | –М | М | М | 0 | 0 |
9) Далее продолжаем решение с нахождения признаков оптимальности решения: 
. Вектор х2 входит в базис и заменяет собой вектор х5. Продолжаем итерации до тех пор, пока не исключим все оценки разложения Δ’’ (т.е. не выведем из базиса все искусственные векторы), а оценки Δ’ не будут соответствовать экстремуму задачи (табл.5.1.6).
Таблица 5.1.6
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ4 | ||
| х5 | 6 | 5 | –1 | –7 | 2 | 1 | 0 | 1,2 | 3 | ||
| х6 | 2 | 3 | –1 | –4 | 1 | 0 | 1 | 2/3 | 2 | ||
| Δ ’ | 0 | 2 | –1 | –8 | 2 | 0 | 0 | ||||
| Δ ’’ | 8M | 8M | –2M | –11M | 3M | 0 | 0 | Θ2 | Θ3 | ||
| х5
| 2 | –1 | 1 | 1 | 0 | 1 | 2 | 2 | |||
| х4 | 2 | 3 | –1 | –4 | 1 | 0 | – | – | |||
| Δ ’ | –4 | –4 | 1 | 0 | 0 | 0 | |||||
| Δ ’’ | 2М | –М | М | М | 0 | 0 | |||||
| х2 | 2 | –1 | 1 | 1 | 0 | ||||||
| х4 | 4 | 2 | 0 | –3 | 1 | ||||||
| Δ ’ | –6 | –3 | 0 | –1 | 0 |
10) В данном примере все коэффициенты в строке оценок Δ’ отрицательны, следовательно, признак оптимальности решения выполнен. Выписываем ответ из соответствующих ячеек симплексной таблицы (табл. 5.1.6):
Ответ: 
Замечание : В том случае, если искусственные переменные нельзя исключить из базиса, задача не имеет решения ввиду несовместности системы ограничений.
5.2. Задача линейного программирования в стандартном виде
В предыдущем примере задача линейного программирования была представлена в канонической форме. Далее рассмотрим пример задачи, система ограничений которой представлена в виде системы неравенств.
ПРИМЕР № 1: 
Решение:
1) Данную задачу сначала необходимо представить в канонической форме. Для этого во все неравенства вида «≤» нужно добавить (а из неравенств вида «≥» нужно вычесть) дополнительные переменные с нумерацией в порядке возрастания, которые войдут в целевую функцию с нулевыми коэффициентами. Затем в уравнения, не имеющие базисных переменных, нужно добавить искусственные переменные, которые войдут в целевую функцию с коэффициентами « 
» (рис. 5.2.1):
|
|
|
Рисунок 5.2.1
После этих действий исходная задача будет представлена в канонической форме записи:
2) Составляем симплексную таблицу. В столбец «Базис» вписываем базисные векторы в порядке следования (х4, х5 и х7) и заполняем таблицу коэффициентами векторов из системы ограничений и оценками разложения векторов системы по базису (табл. 5.2.1):
Таблица 5.2.1
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х7 |
| х 4 | 4 | –1 | 1 | –2 | 1 | 0 | 0 | 0 |
| х5 | 2 | 3 | 2 | 1 | 0 | 1 | 0 | 0 |
| х 7 | 1 | 2 | –1 | 1 | 0 | 0 | –1 | 1 |
| Δ ’ | 0 | –2 | –1 | –1 | 0 | 0 | 0 | 0 |
| Δ ’’ | –M | –2M | M | –M | 0 | 0 | M | 0 |
Вычисляем оценки разложений векторов системы ограничений по базису:
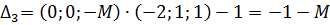
3) Для оценок, показывающих признак неоптимальности решения, вычисляем вспомогательные параметры, заносим их в симплексную таблицу и выбираем наименьший в каждом столбце (табл. 5.2.2):
Таблица 5.2.2
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х7 | Θ1 | Θ3 |
| х 4 | 4 | –1 | 1 | –2 | 1 | 0 | 0 | 0 | – | – |
| х5 | 2 | 3 | 2 | 1 | 0 | 1 | 0 | 0 | 2/3 | 2 |
| х 7 | 1 | 2 | –1 | 1 | 0 | 0 | –1 | 1 | 0,5 | 1 |
| Δ ’ | 0 | –2 | –1 | –1 | 0 | 0 | 0 | 0 | ||
| Δ ’’ | –M | –2M | M | –M | 0 | 0 | M | 0 |
4) Составляем критерий выбора вектора, вводимого в базис, и вектора, выводимого из него: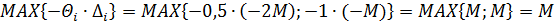 
, следовательно, новый вектор, который войдёт в базис – х3, а выйдет из базиса вектор х7 Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 1 (табл. 5.2.2).
5) Далее применяем элементарные преобразования Жордана-Гаусса и проводим необходимые итерации до получения оптимального решения. Результаты решения представлены в табл. 5.2.3:
Таблица 5.2.3
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х7 | Θ1 | Θ3 |
| х 4 | 4 | –1 | 1 | –2 | 1 | 0 | 0 | 0 | – | – |
| х5 | 2 | 3 | 2 | 1 | 0 | 1 | 0 | 0 | 2/3 | 2 |
| х 7 | 1 | 2 | –1 | 1 | 0 | 0 | –1 | 1 | 0,5 | 1 |
| Δ ’ | 0 | –2 | –1 | –1 | 0 | 0 | 0 | 0 | ||
| Δ ’’ | –M | –2M | M | –M | 0 | 0 | M | 0 | Θ 2 | Θ 6 |
| х4 | 6 | 3 | –1 | 0 | 1 | 0 | –2 | – | – | |
| х5 | 1 | 1 | 3 | 0 | 0 | 1 | 1 | 1/3 | 1 | |
| х 3 | 1 | 2 | –1 | 1 | 0 | 0 | –1 | – | – | |
| Δ ’ | 1 | 0 | –2 | 0 | 0 | 0 | –1 | |||
| х 4 | 8 | 5 | 5 | 0 | 1 | 2 | 0 | |||
| х 6 | 1 | 1 | 3 | 0 | 0 | 1 | 1 | |||
| х 3 | 2 | 3 | 2 | 1 | 0 | 1 | 0 | |||
| Δ ’ | 2 | 1 | 1 | 0 | 0 | 1 | 0 |
6) Все оценки разложения векторов Δi>0, что соответствует условию задачи (максимуму) и говорит о том, что найденное решение единственное, следовательно, найденное решение является оптимальным. Выписываем ответ из соответствующих ячеек симплексной таблицы, не включая в него дополнительные переменные (х4, х5 и х6).
Ответ: 
5.3. Задача линейного программирования с неограниченной целевой функцией
ПРИМЕР: 
Решение:
1) Данную задачу сначала необходимо представить в канонической форме. Для этого во все неравенства вида «≤» нужно добавить (а из неравенств вида «≥» нужно вычесть) дополнительные переменные с нумерацией в порядке возрастания, которые войдут в целевую функцию с нулевыми коэффициентами. Затем в уравнения, не имеющие базисных переменных, нужно добавить искусственные переменные, которые войдут в целевую функцию с коэффициентами « » (рис. 5.3.1):
Рисунок 5.3.1
После этих действий исходная задача будет представлена в канонической форме записи:
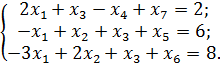
2) Составляем симплексную таблицу. В столбец «Базис» вписываем базисные векторы в порядке следования (х7, х5 и х6) и заполняем таблицу коэффициентами векторов из системы ограничений и оценками разложения векторов системы по базису (табл. 5.3.1):
Таблица 5.3.1
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х7 |
| х7 | 2 | 2 | 0 | 1 | –1 | 0 | 0 | 1 |
| х5 | 6 | –1 | 1 | 1 | 0 | 1 | 0 | 0 |
| х6 | 8 | –3 | 2 | 1 | 0 | 0 | 1 | 0 |
| Δ ’ | 0 | –1 | 1 | 2 | 0 | 0 | 0 | 0 |
| Δ ’’ | –2M | –2M | 0 | –M | M | 0 | 0 | 0 |
Вычисляем оценки разложений векторов системы ограничений по базису:
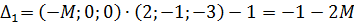
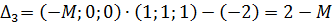
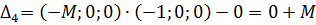
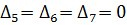
3) Для оценок, показывающих признак неоптимальности решения, вычисляем вспомогательные параметры, заносим их в симплексную таблицу и выбираем наименьший в каждом столбце (табл. 5.3.2):
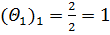
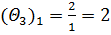
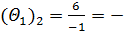
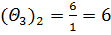
Таблица 5.3.2
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х7 | Θ1 | Θ3 |
| х7 | 2 | 2 | 0 | 1 | –1 | 0 | 0 | 1 | 1 | 2 |
| х5 | 6 | –1 | 1 | 1 | 0 | 1 | 0 | 0 | – | 6 |
| х6 | 8 | –3 | 2 | 1 | 0 | 0 | 1 | 0 | – | 8 |
| Δ ’ | 0 | –1 | 1 | 2 | 0 | 0 | 0 | 0 | ||
| Δ ’’ | –2M | –2M | 0 | –M | M | 0 | 0 | 0 |
4) Составляем критерий выбора вектора, вводимого в базис, и вектора, выводимого из него: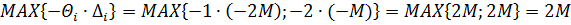 
, следовательно, новый вектор, который войдёт в базис – х3, а выйдет из базиса вектор х7 Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 1 (табл. 5.3.2).
5) Далее применяем элементарные преобразования Жордана-Гаусса и проводим необходимые итерации до получения оптимального решения. Результаты решения представлены в табл. 5.3.3:
Таблица 5.3.3
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х7 | Θ1 | Θ3 |
| х7 | 2 | 2 | 0 | 1 | –1 | 0 | 0 | 1 | 1 | 2 |
| х5 | 6 | –1 | 1 | 1 | 0 | 1 | 0 | 0 | – | 6 |
| х6 | 8 | –3 | 2 | 1 | 0 | 0 | 1 | 0 | – | 8 |
| Δ ’ | 0 | –1 | 1 | 2 | 0 | 0 | 0 | 0 | ||
| Δ ’’ | –2M | –2M | 0 | –M | M | 0 | 0 | 0 | Θ1 | |
| х3 | 2 | 2 | 0 | 1 | –1 | 0 | 0 | 1 | ||
| х5 | 4 | –3 | 1 | 0 | 1 | 1 | 0 | – | ||
| х6 | 6 | –5 | 2 | 0 | 1 | 0 | 1 | – | ||
| Δ ’ | –4 | –5 | 1 | 0 | 2 | 0 | 0 | Θ4 | ||
| х1 | 1 | 1 | 0 | 0,5 | –0,5 | 0 | 0 | – | ||
| х5 | 7 | 0 | 1 | 1,5 | –0,5 | 1 | 0 | – | ||
| х6 | 11 | 0 | 2 | 2,5 | –1,5 | 0 | 1 | – | ||
| Δ ’ | 1 | 0 | 1 | 2,5 | –0,5 | 0 | 0 |
6) Оценка Δ4<0, что не соответствует условию задачи (максимуму) и говорит о том, что найденное решение не оптимально, но все вспомогательные параметры для этой оценки отрицательны (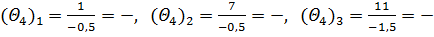 
). Следовательно, продолжить решение невозможно, и это говорит о том, что целевая функция не ограничена.
Ответ: 
5.4. Задача линейного программирования с двумя оптимальными решениями
ПРИМЕР № 1: 
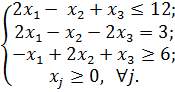
Решение:
1) Представляем задачу в канонической форме:
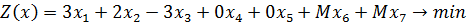
2) Составляем симплексную таблицу (табл. 5.4.1):
Таблица 5.4.1
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х 7 | Θ 1 | Θ 2 |
| х 4 | 12 | 2 | –1 | 1 | 1 | 0 | 0 | 0 | 6 | – |
| х 6 | 3 | 2 | –1 | –2 | 0 | 0 | 1 | 0 | 1,5 | – |
| х 7 | 6 | –1 | 2 | 1 | 0 | –1 | 0 | 1 | – | 3 |
| Δ ’ | 0 | –3 | –2 | 3 | 0 | 0 | 0 | 0 | ||
| Δ ’’ | 9M | M | M | –M | 0 | –M | 0 | 0 |
3) Данная задача решается на минимум, следовательно, отмечаем все оценки 
. Для найденных оценок вычисляем вспомогательные параметры и заносим их в симплексную таблицу. Выбираем минимальный параметр в каждом столбце и отмечаем его (табл. 5.4.1):
4) Составляем критерий выбора вектора, вводимого в базис, и вектора, выводимого из него: 
, следовательно, новый вектор, который войдёт в базис – х2, а выйдет из базиса вектор х7 Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 2 (табл. 5.4.1).
5) Далее применяем элементарные преобразования Жордана-Гаусса и проводим необходимые итерации до получения оптимального решения. Результаты решения представлены в табл. 5.4.2:
Таблица 5.4.2
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х 7 | Θ 1 | Θ 2 |
| х 4 | 12 | 2 | –1 | 1 | 1 | 0 | 0 | 0 | 6 | – |
| х 6 | 3 | 2 | –1 | –2 | 0 | 0 | 1 | 0 | 1,5 | – |
| х 7 | 6 | –1 | 2 | 1 | 0 | –1 | 0 | 1 | – | 3 |
| Δ ’ | 0 | –3 | –2 | 3 | 0 | 0 | 0 | 0 | ||
| Δ ’’ | 9M | M | M | –M | 0 | –M | 0 | 0 | Θ 1 | |
| х 4 | 15 | 1,5 | 0 | 1,5 | 1 | –0,5 | 0 | 10 | ||
| х 6 | 6 | 1,5 | 0 | –1,5 | 0 | –0,5 | 1 | 4 | ||
| х2 | 3 | –0,5 | 1 | 0,5 | 0 | –0,5 | 0 | – | ||
| Δ ’ | 6 | –4 | 0 | 4 | 0 | –1 | 0 | |||
| Δ ’’ | 6М | 1,5М | 0 | –1,5М | 0 | –0,5М | 0 | Θ3 | ||
| х 4 | 9 | 0 | 0 | 3 | 1 | 0 | 3 | |||
| х1 | 4 | 1 | 0 | –1 | 0 | –1/3 | – | |||
| х2 | 5 | 0 | 1 | 0 | 0 | –2/3 | – | |||
| Δ ’ | 22 | 0 | 0 | 0 | 0 | –7/3 | ||||
| х3 | 3 | 0 | 0 | 1 | 1/3 | 0 | ||||
| х1 | 7 | 1 | 0 | 0 | 1/3 | –1/3 | ||||
| х2 | 5 | 0 | 1 | 0 | 0 | –2/3 | ||||
| Δ ’ | 22 | 0 | 0 | 0 | 0 | –7/3 |
6) Все оценки разложения векторов 
, что соответствует условию задачи (минимуму), но говорит о том, что найденное решение не единственно возможное, следовательно, выписываем два оптимальных решения.
Ответ: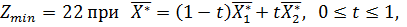 
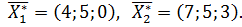
5.5. Задача линейного программирования с тремя оптимальными решениями
ПРИМЕР № 1: 
Решение:
1) Представляем задачу в канонической форме:
2) Составляем симплексную таблицу (табл. 5.5.1):
Таблица 5.5.1
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х 7 | х 8 | х 9 | Θ 1 | Θ 2 | Θ 3 |
| х 7 | 6 | 3 | 2 | 3 | –1 | 0 | 0 | 1 | 0 | 0 | 2 | 3 | 2 |
| х 8 | 5 | 1 | 1 | 1 | 0 | –1 | 0 | 0 | 1 | 0 | 5 | 5 | 5 |
| х 9 | 6 | 2 | 3 | 2 | 0 | 0 | –1 | 0 | 0 | 1 | 3 | 2 | 3 |
| Δ ’ | 0 | –1 | –1 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| Δ ’’ | 17М | 6М | 6М | 6М | –М | –М | –М | 0 | 0 | 0 |
3) Данная задача решается на минимум, следовательно, отмечаем все оценки . Для найденных оценок вычисляем вспомогательные параметры и заносим их в симплексную таблицу. Выбираем минимальный параметр в каждом столбце и отмечаем его (табл. 5.5.1):
4) Составляем критерий выбора вектора, вводимого в базис, и вектора, выводимого из него: 
, следовательно, новый вектор, который войдёт в базис – х1, а выйдет из базиса вектор х7. Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 3.
5) Далее применяем элементарные преобразования Жордана-Гаусса и проводим необходимые итерации до получения оптимального решения. Результаты решения представлены в табл. 5.5.2:
Таблица 5.5.2
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х 7 | х 8 | х 9 | Θ 1 | Θ 2 | Θ 3 |
| х 7 | 6 | 3 | 2 | 3 | –1 | 0 | 0 | 1 | 0 | 0 | 2 | 3 | 2 |
| х 8 | 5 | 1 | 1 | 1 | 0 | –1 | 0 | 0 | 1 | 0 | 5 | 5 | 5 |
| х 9 | 6 | 2 | 3 | 2 | 0 | 0 | –1 | 0 | 0 | 1 | 3 | 2 | 3 |
| Δ ’ | 0 | –1 | –1 | –1 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| Δ ’’ | 17М | 6М | 6М | 6М | –М | –М | –М | 0 | 0 | 0 | Θ 2 | Θ4 | |
| х 1 | 2 | 1 | 2/3 | 1 | –1/3 | 0 | 0 | 0 | 0 | 3 | – | ||
| х 8 | 3 | 0 | 1/3 | 0 | 1/3 | –1 | 0 | 1 | 0 | 9 | 9 | ||
| х 9 | 2 | 0 | 5/3 | 0 | 2/3 | 0 | –1 | 0 | 1 | 6/5 | 3 | ||
| Δ ’ | 2 | 0 | –1/3 | 0 | –1/3 | 0 | 0 | 0 | 0 | ||||
| Δ ’’ | 5М | 0 | 2М | 0 | М | –М | –М | 0 | 0 | Θ6 | |||
| х1 | 3 | 1 | 1,5 | 1 | 0 | 0 | –0,5 | 0 | – | ||||
| х 8 | 2 | 0 | –0,5 | 0 | 0 | –1 | 0,5 | 1 | 4 | ||||
| х4 | 3 | 0 | 2,5 | 0 | 1 | 0 | –1,5 | 0 | – | ||||
| Δ ’ | 3 | 0 | 0,5 | 0 | 0 | 0 | –0,5 | 0 | |||||
| Δ ’’ | 2М | 0 | –0,5М | 0 | 0 | –М | 0,5М | 0 | Θ 2 | Θ 3 | |||
| х1 | 5 | 1 | 1 | 1 | 0 | –1 | 0 | 5 | 5 | ||||
| х6 | 4 | 0 | –1 | 0 | 0 | –2 | 1 | – | – | ||||
| х4 | 9 | 0 | 1 | 0 | 1 | –3 | 0 | 9 | – | ||||
| Δ ’ | 5 | 0 | 0 | 0 | 0 | –1 | 0 | Θ 3 | |||||
| х2 | 5 | 1 | 1 | 1 | 0 | –1 | 0 | 5 | |||||
| х6 | 9 | 1 | 0 | 1 | 0 | –3 | 1 | 9 | |||||
| х4 | 4 | –1 | 0 | –1 | 1 | –2 | 0 | – | |||||
| Δ ’ | 5 | 0 | 0 | 0 | 0 | –1 | 0 | ||||||
| х3 | 5 | 1 | 1 | 1 | 0 | –1 | 0 | ||||||
| х6 | 4 | 0 | –1 | 0 | 0 | –2 | 1 | ||||||
| х4 | 13 | 0 | 0 | 0 | 1 | –5 | 1 | ||||||
| Δ ’ | 5 | 0 | 0 | 0 | 0 | –1 | 0 |
6) Все оценки разложения векторов , что соответствует условию задачи (минимуму), но говорит о том, что найденное решение не единственно возможное, следовательно, выписываем три оптимальных решения.
Ответ:
5.6. Задача линейного программирования с несовместной системой ограничений
ПРИМЕР № 1: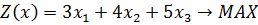 
Решение:
1) Представляем задачу в канонической форме:
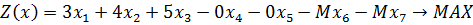
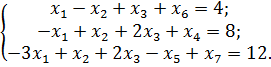
2) Составляем симплексную таблицу (табл. 5.6.1):
Таблица 5.6.1
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х 7 | Θ3 |
| х6 | 4 | 1 | –1 | 1 | 0 | 0 | 1 | 0 | 4 |
| х 4 | 8 | –1 | 1 | 2 | 1 | 0 | 0 | 0 | 4 |
| х 7 | 12 | –3 | 1 | 2 | 0 | –1 | 0 | 1 | 6 |
| Δ ’ | 0 | –3 | –4 | –5 | 0 | 0 | 0 | 0 | |
| Δ ’’ | –16M | 2M | 0 | –3M | 0 | М | 0 | 0 |
3) Данная задача решается на максимум, следовательно, отмечаем все оценки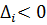 
. Для найденных оценок вычисляем вспомогательные параметры и заносим их в симплексную таблицу. Выбираем минимальный параметр в каждом столбце и отмечаем его (табл. 5.6.1).
4) Критерий выбора в данном случае составлять не нужно. Новый вектор, который войдёт в базис – х3, а выйдет из базиса вектор х6. Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 1 (табл. 5.6.1).
5) Далее применяем элементарные преобразования Жордана-Гаусса и проводим необходимые итерации до получения оптимального решения. Результаты решения представлены в табл. 5.6.2:
Таблица 5.6.2
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | х 7 | Θ3 |
| х6 | 4 | 1 | –1 | 1 | 0 | 0 | 1 | 0 | 4 |
| х 4 | 8 | –1 | 1 | 2 | 1 | 0 | 0 | 0 | 4 |
| х 7 | 12 | –3 | 1 | 2 | 0 | –1 | 0 | 1 | 6 |
| Δ ’ | 0 | –3 | –4 | –5 | 0 | 0 | 0 | 0 | |
| Δ ’’ | –16M | 2M | 0 | –3M | 0 | М | 0 | 0 | Θ2 |
| х3 | 4 | 1 | –1 | 1 | 0 | 0 | 0 | – | |
| х4 | 0 | –3 | 3 | 0 | 1 | 0 | 0 | 0 | |
| х7 | 4 | –5 | 3 | 0 | 0 | –1 | 1 | 4/3 | |
| Δ ’ | 20 | 2 | –9 | 0 | 0 | 0 | 0 | ||
| Δ ’’ | –4М | 5М | –3М | 0 | 0 | М | 0 | ||
| х3 | 4 | 0 | 0 | 1 | 1/3 | 0 | 0 | ||
| х2 | 0 | –1 | 1 | 0 | 1/3 | 0 | 0 | ||
| х7 | 4 | –2 | 0 | 0 | –1 | –1 | 1 | ||
| Δ ’ | 20 | –7 | 0 | 0 | 3 | 0 | 0 | ||
| Δ ’’ | –4М | 2М | 0 | 0 | М | М | 0 |
6) Все оценки разложения векторов , что соответствует условию задачи (максимуму), но в решении остался неисключённым искусственный вектор х7, что говорит о несовместности системы ограничений.
Ответ: Задача не имеет решения ввиду несовместности системы ограничений.
5.7. Задания для самостоятельного решения
1) 
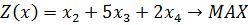
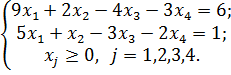
Ответ: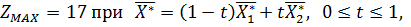 
2) 
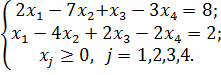
Ответ: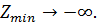 
3) 
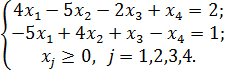
Ответ: Система ограничений несовместна.
4) 
Ответ: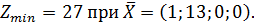 
5) 
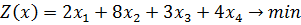
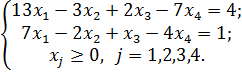
Ответ: 
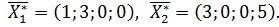
6) 
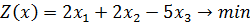
Ответ: 
7) 
Ответ: 
8) 
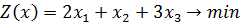
Ответ: 
9) 
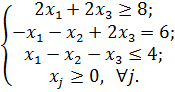
Ответ: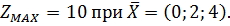 
10) 
Ответ: 
11) 
Ответ: 
12) 
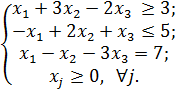
Ответ: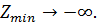
13) 
Ответ: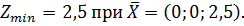 
14) 
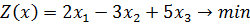
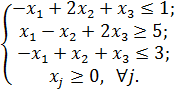
Ответ: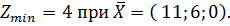 
15)
Ответ: 
16) 
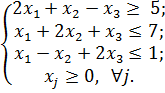
Ответ: 
6. Транспортная задача линейного программирования
Термин «транспортная задача» в линейном программировании объединяет широкий круг задач с единой математической моделью (которые могут быть решены симплекс-методом). Однако, обычно транспортная задача имеет большое количество переменных, поэтому решение её симплекс-методом достаточно громоздко. С другой стороны, матрица системы ограничений транспортной задачи весьма своеобразна, поэтому для её решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить последовательность опорных решений, которая завершается оптимальным решением.[1]
Постановка транспортной задачи
Однородный груз (который может быть перевезён одним видом транспорта) сосредоточен у т поставщиков (например, на нескольких складах, предприятиях, заводах, фабриках и.т.п.) в объёмах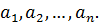 
Данный груз необходимо доставить п потребителям (например, в несколько магазинов, комбинатов, дилерских центров и.т.п.) в объёмах 
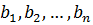(в зависимости от заявленных потребностей и отличных от объёмов продукции, находящихся у поставщиков). Известны коэффициенты 
– стоимости перевозки единицы груза от каждого поставщика каждому потребителю.[2] Эти коэффициенты рассчитываются путём суммирования затрат на топливо, амортизацию оборудования, заработную плату, логистические расходы и т.п. и отношения их к нелинейной протяжённости пути каждой перевозки (учитывая и километраж, и затраченное время в пути). Чем ближе поставщик расположен к потребителю, тем, соответственно, меньше будет составлять стоимость перевозки.
Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью, а общие суммарные затраты на перевозку всех грузов минимальны.[3]
Исходные данные транспортной задачи обычно записываются в таблице следующего вида (табл. 6.1):
Таблица 6.1
Математическая модель транспортной задачи
Переменными транспортной задачи являются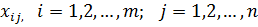 
– объёмы перевозок от каждого i-го поставщика каждому j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок:
Так как произведение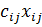 
определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны 
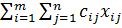. По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция задачи имеет вид:
(6.1)
Система ограничений задачи состоит из двух групп уравнений. Первая группа из т уравнений описывает тот факт, что запасы всех т поставщиков вывозятся полностью. Вторая группа из п уравнений выражает требование удовлетворить запросы всех п потребителей полностью. Учитывая условие неотрицательности объёмов перевозок, система ограничений задачи будет выглядеть следующим образом:
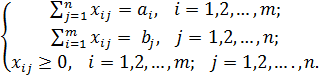(6.2)
В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е. 
Такая задача называется задачей с правильным балансом, а модель задачи – закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а модель задачи – открытой.
Опорным решением транспортной задачи называется любое допустимое решение, для которого векторы условий, соответствующие положительным координатам, линейно независимы. Ввиду того, что ранг системы ограничений задачи равен (т+п-1), опорное решение не может иметь отличных от нуля координат (т.е. перевозок) более (т+п-1).[1]
Дата добавления: 2020-11-15; просмотров: 294; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!