Акустическая энергия, поток энергии, вектор Умова
Фазовая скорость в газах и жидкостях
Прежде всего, остановимся на определении скорости звука в идеальных газах, воспользовавшись формулой (1.3.10)
.
Связь между давлением p и плотностью r для адиабатического процесса определяется уравнением Пуассона 
, откуда несложно найти производную 
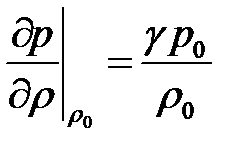и скорость звука в идеальных газах
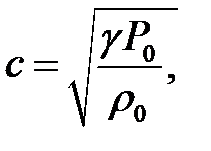(2.2.1)
где P0и 
− статические значения давления и плотности газа, g = Ср/Сn − постоянная адиабаты или коэффициент Пуассона.
Выражение (2.2.1) получено в предположении адиабатичности процесса распространения волны в среде, то есть, между участками сжатия и разряжения в волне теплообмена нет, и температура не успевает выравниваться.
В первом приближении скорость звука не зависит ни от частоты, ни от его амплитуды. Это в большей степени справедливо для одноатомных газов, но для газов, молекулы которых состоят более чем из одного атома, такие зависимости имеют место. Если скорость звука в среде зависит от частоты, то говорят, что в среде имеет место дисперсия скорости звука.
Зависимость скорости звука от температуры для идеальных газов можно найти, если воспользоваться уравнением Менделеева-Клапейрона
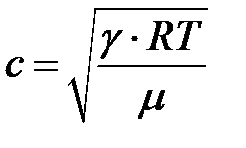, (2.2.2)
где R − универсальная газовая постоянная, Т − абсолютная температура, m − молярная масса.
Из формулы (2.2.2) следует, что c~ 
и не зависит от давления. Для воздуха с = 333 м/с (при давлении одна атмосфера и температуре 0оС). При увеличении температуры скорость звука в воздухе увеличивается примерно на 0,6 м/сК.
|
|
|
Приведенные выше формулы (2.2.1) и (2.2.2) получены на основе решения уравнений гидродинамики и термодинамического уравнения состояния газа при акустическом числе Маха Ма << 1.
В газах и парах умеренной плотности скорость звука в первом приближении определяется при помощи формул (2.2.1) и (2.2.2), причем обычно величина с уменьшается с ростом молярной массы. Наибольшее значение скорости звука наблюдается в водороде с = 1284 м/с (Т = 273 К,
Р0 = 1,01×105 Па), а наименьшее значение у ряда веществ, которые при тех же условиях находятся в газообразном состоянии. Например, в йодистом водороде с = 157 м/с. Температурные градиенты скорости звука для большинства газов находятся в интервале 0,3...0,8 м/сК. Исключение составляют только очень плотные газы (например, в парах хлороформа D ст = 0,24 м/сК) и очень легкие газы (для водорода Dст = 2,3 м/сК).
Формула (2.2.2) имеет большое практическое значение, так как она часто используется для определения молекулярной массы и коэффициента Пуассона газов. Отметим, что для того, чтобы в формуле (2.2.2) осталась одна неизвестная величина, коэффициент Пуассона в ней заменяют известным из термодинамики выражением g = 1 + R / m CV .
|
|
|
В случае реальных газов (газ Ван-дер-Ваальса) уравнение состояния газа имеет вид
, (2.2.3)
где a и b − постоянные Ван-дер-Ваальса, V − молярный объем.
Из термодинамики известно, что это уравнение хорошо выполняется для многих газов и паров в широком интервале температур и большом диапазоне давлений. Использование уравнения (2.2.3) позволяет для скорости звука в реальных газах найти следующее выражение
, (2.2.4)
где с − скорость звука в идеальном газе, вычисляемая по формулам (2.2.1) и (2.2.2).
При малых плотностях газа формула (2.2.3) упрощается и принимает вид
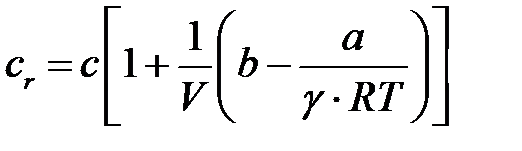, (2.2.5)
где g − коэффициент Пуассона для идеального газа.
Из выражения (2.2.5) видно, что скорость звука монотонно растет с ростом температуры. Температурный коэффициент квадрата скорости звука в реальных газах может быть найден из выражения
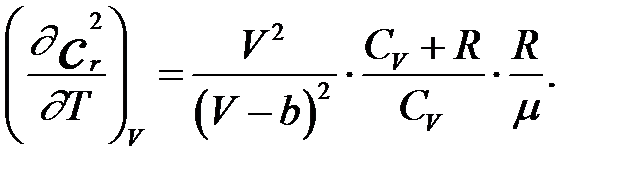(2.2.6)
При использовании формулы (2.2.6) следует иметь ввиду то, что она получена в предположении независимости констант а и b от температуры и статического давления. В действительности такие зависимости имеют место, но в первом приближении ими можно пренебречь.
|
|
|
Жидкости занимают промежуточное положение между твердыми телами и газами, обладая, в отличие от твердых тел, лишь близким порядком. Теория жидкого состояния до сих пор еще не разработана. По этой причине теоретические расчеты скорости звука в жидкостях оказываются в еще меньшей степени обоснованными, чем для реальных газов. В литературе имеются только эмпирические и полуэмпирические формулы для расчета скорости звука в жидкостях, дающие связь между с и макроскопическими параметрами среды.
При проведении океанологических исследований показано [4,5], что абсолютное значение скорости звука в морской воде может измениться в пределах от 1400 до 1600 м/с. Среднее значение скорости звука в океане принимают равным 1500 м/с. Это же значение скорости звука принимают при проведении предварительных расчетов в гидроакустике.
Часто в акустических расчетах для определения значений скорости звука в воде используют следующую эмпирическую формулу
, м/с, (2.2.7)
где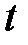 
– температура морской воды в 
С, S – соленость МВ в промилле.
Выражение (2.2.7) дает следующие значения абсолютных ошибок при определении скорости звука в МВ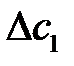 
= 1,5 м/с для 10 
С и 
£ 6,0 м/с для
|
|
|
30 
С.
В тех случаях, когда необходимо учесть глубину моря для расчетов скорости звука в морской воде принимают другое эмпирическое выражение 
, (2.2.8)
где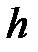 
– глубина в метрах.
Необходимо отметить, что в океанографической литературе имеются и другие формулы для расчета скорости звука в морской воде. Кроме того, имеются также весьма подробные таблицы, в которых представлены значения скорости звука в морской воде в зависимости от температуры, статического давления и солености воды.
Акустическая энергия, поток энергии, вектор Умова
При возбуждении звуковых волн энергия от источника поступает в среду. Благодаря этой энергии и возникает колебательное движение частиц среды. Энергия этих колебаний может передаваться телам, помещенным в звуковое поле, то есть приемникам звука. Именно этот процесс – передача энергии и является рабочим процессом акустики, в конечном счете. По этой причине понятие об акустической энергии относится к основным понятиям акустики.
Под акустической энергией понимается такая форма механической энергии, которая переносится волной в упругой среде с распределенными массой и упругостью и проявляется в любой точке этой среды в виде изменения механических напряжений и давлений, наблюдавшихся в этой точке при отсутствии акустической энергии.
Энергию звукового поля можно характеризовать двумя величинами: плотностью звуковой энергии и интенсивностью звука.
Плотность звуковой энергии это энергия, отнесенная к единице объема, занятого акустическим полем.
Интенсивность звука – энергия, переносимая звуковой волной через единичную площадку, расположенную перпендикулярно направлению распространения волны, за единицу времени.
Рассмотрим теперь в самом общем виде соотношения между этими величинами, не касаясь деталей распространения волны и вида возбуждения, которые будут рассмотрены позже.
Как уже отмечалось, одним из основных уравнений акустики является уравнение движения (уравнение Эйлера), которое запишем в виде
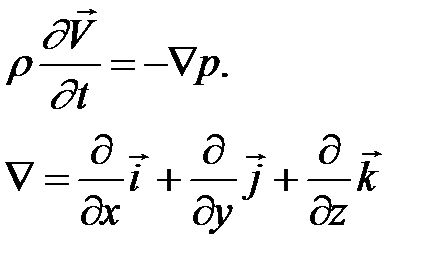(2.3.1)
Преобразуем это уравнение, умножив его слева на вектор колебательной скорости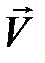 
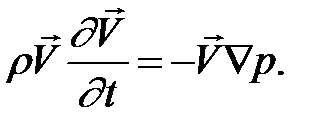(2.3.2)
Применим оператор 
к произведению ( 
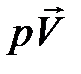), получим
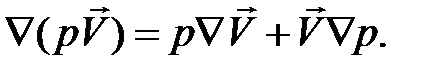
Откуда выразим правую часть (2.3.2)
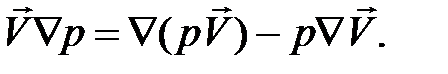
Теперь уравнение (2.3.2) принимает вид
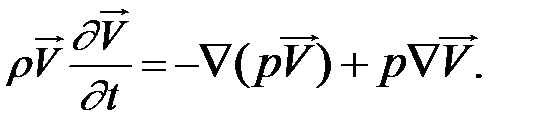(2.3.3)
Далее воспользуемся уравнением непрерывности (1.3.21), подставив его в (2.3.3)
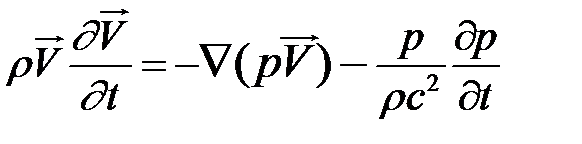или
(2.3.4)
В левой части уравнения (2.3.4) первое слагаемое содержит произведение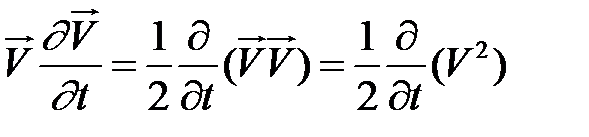 
. По аналогии, второе слагаемое запишем в виде 
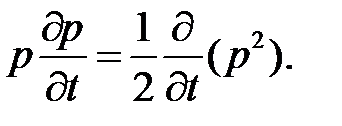В правой части уравнения (2.3.4) введем вектор 
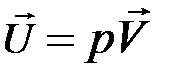. После подстановки получим
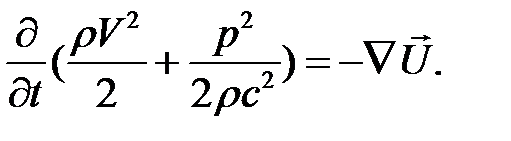(2.3.5)
Величина, стоящая в скобках уравнения (2.3.5), представляет собой сумму двух видов акустической энергии в единице объема вещества:
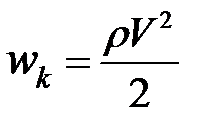- объемная плотность кинетической энергии;
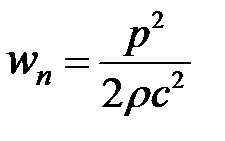- объемная плотность потенциальной энергии (напомним, что в знаменателе 
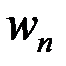величина 
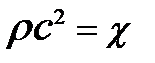является характеристикой упругости среды).
Объемная плотность полной акустической энергии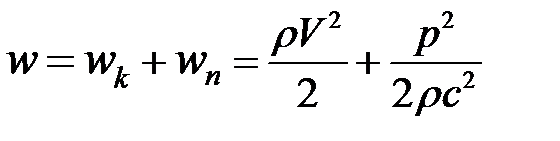 
. Очевидно, что акустическая энергия в объеме v вещества может быть вычислена в виде интегральной суммы
(2.3.6)
Скорость изменения акустической энергии (акустическая мощность) равна
(2.3.7)
Введенный вектор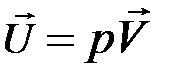 
в правой части уравнения (2.3.5) носит название вектора Умова. Чтобы понять физический смысл вектора Умова,
определим сначала его размерность: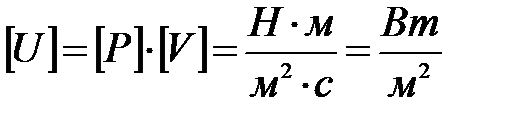 
. Итак, можно
сказать, что вектор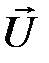 
определяется энергией, переносимой волной в единицу времени (мощность потока акустической энергии) через единицу поверхности по нормали к этой поверхности. Величину 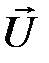называют также плотность потока мощности.
После подстановки уравнения (2.3.5) в (2.3.7), а затем используя теорему Гаусса для преобразования объемного интеграла в поверхностный, получим
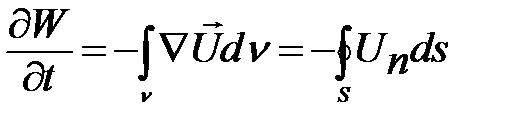(2.3.8)
Уравнение (2.3.8) отражает интегральный закон сохранения энергии для акустической волны: изменение акустической энергии в объеме v обусловлено потоком акустической мощности через замкнутую поверхность s, охватывающую этот объем. Если 
, то поток мощности положительный (из объема v), и наоборот.
Дата добавления: 2020-11-15; просмотров: 344; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!