В45 ОДМ. ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ МАТ. ОЖИДАНИЯ
В 41 ОДМ. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ МАТ. ОЖИДАНИЯ.
В качестве примера построим доверительный интервал для мат.ожидания m величины х. При решении этой задачи воспользуемся тем, что величина m* представляет собой сумму n независимый одинаково распределенных СВ xi и согласно центральной опред. Теореме при достаточно больших n ее закон распределения близок к нормальному. На практике уже при количестве опытов 10, 20 закон распределения M* можно приближенно считать нормальным.
Таким образов имеем право принять гипотезу о нормальном распределении M* Параметры этого закона мат.ожидание n и дисперсия D/n,где Д-дисперсия СВХ значение которого известны. Найдем такую величину 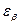 , для которой
, для которой

Учитывая, что закон распределения нормальный, получим
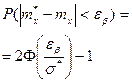 , где
, где 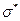 -среднее квадратическое
-среднее квадратическое
Ф-значение функции нормированного распределения
Из последних 2х уравнений находим значение 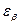 :
:
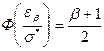
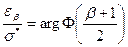
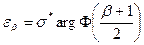
Где arg Ф( 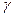 ) -такое значение аргумента при котором нормальная функция распределения равна
) -такое значение аргумента при котором нормальная функция распределения равна 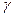 .
.
Величина 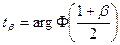 -квантильный множитель, определяет для нормального закона число средних квадратических отклонений которые нужно отложить вправо и влево от центра рассеивания для того, чтобы вероятность попадания в полученный интервал была равна
-квантильный множитель, определяет для нормального закона число средних квадратических отклонений которые нужно отложить вправо и влево от центра рассеивания для того, чтобы вероятность попадания в полученный интервал была равна 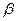 .
.
Используя значение 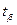 , доверительный интервал для мат.ожидания запишем:
, доверительный интервал для мат.ожидания запишем: 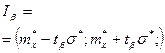
В42 ОДМ. ПОСТОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ ДИСПЕРСИИ.
|
|
|
Пусть произведению n независимых опытов над случайной величиной Х с неизвестными параметрами m и D для дисперсии получена несмещенная оценка.

Из формулы (1) видно что оценка Д* представляет сумму n СВ вида:
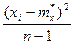
Эти величины и является независимыми. Т.к. в любую из них входит оценка m* зависящая от всех остальных.
Однако при увеличении n закон распределения суммы приближается к нормальному и при уже может считаться нормальным.
При построении довер. Интервала примем гипотезу о нормальном законе распределения Д*, так 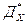 несмещенная, то матожидание M[
несмещенная, то матожидание M[ 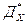 ]=Дx
]=Дx
Дисперсию оценки можно опред. по формуле : 
Вместо 4 центр. момента в этом выражении можно воспользоваться его оценкой 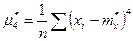 .
.
Однако точность такой оценки очень невысокая. Для норм. з-на распр-я случ. величины Х  выражается через дисперсию.
выражается через дисперсию.
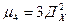
Чтобы воспользоваться формулой для оценки Дх*  в нее нужно поставить хотя бы приближенные значения параметра Дх. Можно воспользоваться например оценкой Д* тогда для норм. з-на получим
в нее нужно поставить хотя бы приближенные значения параметра Дх. Можно воспользоваться например оценкой Д* тогда для норм. з-на получим
В этом случае доверит.интервал для дисперсии СВ Х имеет вид
В43 ОДМ. СТАТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ.
|
|
|
Под гипотезой Н будет понимать некоторое предположение об свойствах случайной величины Х
Путем статической проверки устанавливают на сколько данные полученные из n опытов согласуются с высказанной гипотезой,т.е. можно ли на их основаниях принять или отвергнуть гипотезу. Абсолютно достоверное решение относительно рассматриваемой гипотезы получить нельзя. При проверки гипотезы могут быть допущены ошибки 1 и 2 рода.
Ошибка 1 рода состоит в том, что будет отвергнута правильная гипотеза. Вероятность такой ошибки назыв. Уравнением значимости и часто обозначается 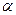 .При проверке гипотезы величина должна быть выбрана экспериментально.
.При проверке гипотезы величина должна быть выбрана экспериментально.
Ошибка 2 рода состоит в том, что будет принята непрвильная гипотеза. Вероятность такой ошибки часто выражают через 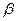 .
.
Для проверки гипотез используют случайную величину полученную по опред. Правилам и называемую статическим критерием. Совокупность значения критерия при котором проверяемую гипотезу отвергают назыв. Критической областью.
Процедура проверки состоит в след.:
1)выбирается критерий Z и рассчитывается его значение исходя из опытных данных
2)устанавливается критическая область К в которую в случае справедливости гипотезы Н значение Z может попасть только с малой вероятностью
|
|
|
3)Если значение Z попало в область К, гипотеза Н отклоняется, в противном случае считают что оснований для отклонения нет.
Критическая область может быть:
-односторонней-когда проверяется условие 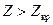 при
при 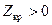 или
или 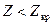 при
при 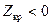
-двусторонней-когда проверяются условия  при
при 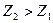
Критические точки Zкр ищут исходя из соотн-й:
-для односторонней крит. Обл-ти
-для двусторонней крит. Обл-ти
В44 ОДМ.ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДИСПЕРСИЙ НОРМАЛЬНЫХ СОВОКУПНОСТЕЙ.
По независимым малым выборкам из нормальных генеральных совокупностей объемами n1 и n2 (n1<30 и n2<30) найдены выборочные средние 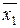 и
и 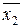 и выборочные дисперсии D*1 и D*2. Генеральные дисперсии неизвестны, но принята гипотеза об их равенстве. Для того чтобы при заданном уровне значимости a проверить гипотезу Н0: М(x 1)=М(x 2) о равенстве математических ожиданий (генеральных средних) нормальных совокупностей в случае малых независимых выборок при конкурирующей гипотезе Н1: М(x 1) ¹М(x 2), необходимо вычислить значение критерия по формуле:
и выборочные дисперсии D*1 и D*2. Генеральные дисперсии неизвестны, но принята гипотеза об их равенстве. Для того чтобы при заданном уровне значимости a проверить гипотезу Н0: М(x 1)=М(x 2) о равенстве математических ожиданий (генеральных средних) нормальных совокупностей в случае малых независимых выборок при конкурирующей гипотезе Н1: М(x 1) ¹М(x 2), необходимо вычислить значение критерия по формуле:
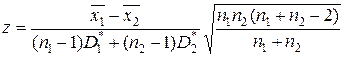
и по таблице распределения Стьюдента, исходя из заданного уровня значимости a и числа степеней свободы k = n 1 + n 2 -2, найти критическую точку zкр(a, k). Если |z|< zкр(a, k) нет оснований отвергнуть гипотезу Н0.
|
|
|
В45 ОДМ. ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ МАТ. ОЖИДАНИЯ
По независимым выборкам из нормальных генеральных совокупностей объемами n1 и n2 найдены выборочные дисперсии D*1 и D*2, причем D*1>D*2. Для того, чтобы при заданном уровне значимости a проверить гипотезу Н0: D*1=D*2 о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе Н1: D*1¹D*2, необходимо вычислить значение критерия как отношение максимальной из выборочных дисперсий к минимальной:
F= D*max/D*min
и по таблице распределения Фишера, исходя из заданного уровня значимости a и чисел степеней свободы большей выборочной дисперсии k1= n1-1 и меньшей выборочной дисперсии k2= n2-1 найти критическую точку Fкр(a/2, k1, k2). Если F<Fкр нет оснований отвергнуть гипотезу Н0.
Дата добавления: 2020-04-25; просмотров: 200; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
