Метод решения уравнений путем нахождения и исследования ОДЗ.
Иррациональные уравнения.
1.Решить, используя свойство корня 2.Решить, используя свойство корня
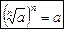четной степени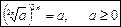 
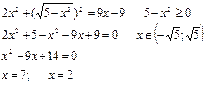
3.Уравнение вида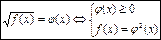 
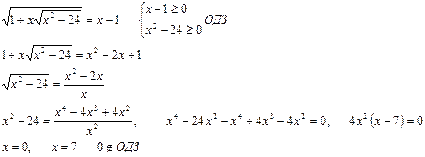
4. Уравнение вида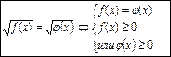 
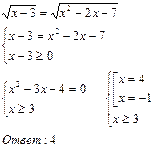
5. Уравнение вида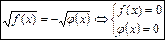 
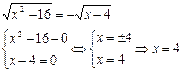
6. Уравнение вида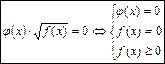 
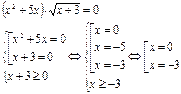
Введение новой переменной.
| 
| 
|
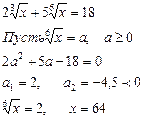
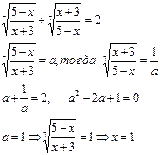
Решить уравнение: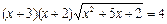 
.
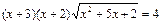
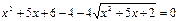
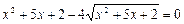. Замена 
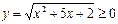приводит
к уравнению y2-4y=0
.
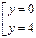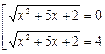
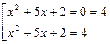
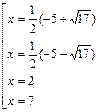
Так как были использованы только равносильные переходы, отдельная проверка корней, а также нахождение ОДЗ не требуется.
Ответ:2;7; 
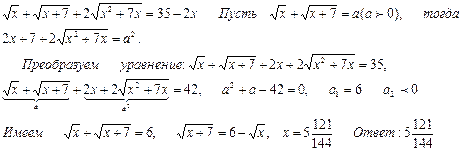
№3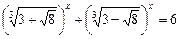 
Воспользуемся равенством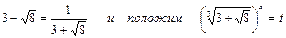 
. Тогда уравнение примет вид 
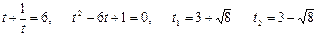. Исходное уравнение равносильно совокупности уравнений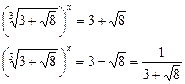 
Отсюда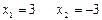 
. Ответ: 3; -3.
Решить уравнение, используя разложение на множители.
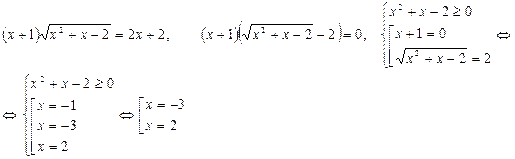
Решить уравнение методом умножения на сопряженное выражение.
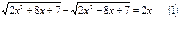
Умножим обе части уравнения на сопряженное: 
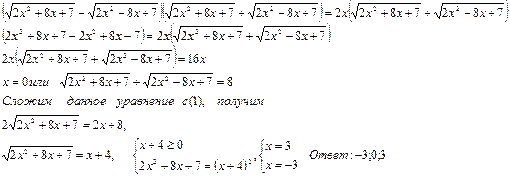
Решить уравнение методом выделения полного квадрата
Решить уравнение, разложением на множители подкоренного выражения.
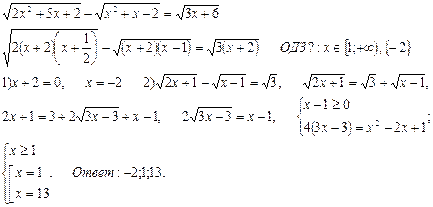
Решить уравнение методом введения двух переменных.
Уравнения, содержащие знак модуля.
№1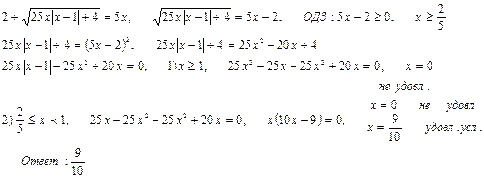 
№2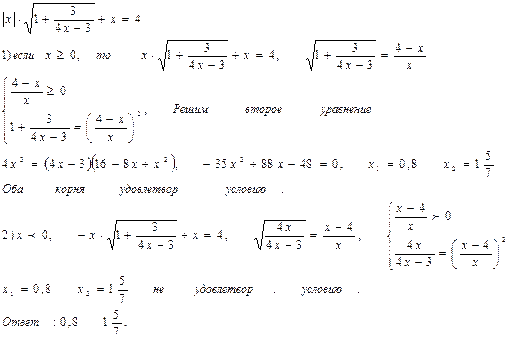 
№3.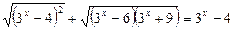 
Так как левая часть уравнения неотрицательна, то уравнение может иметь решения только в том случае, когда правая часть тоже неотрицательна.
Поэтому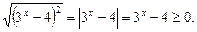 
После упрощений уравнение принимает вид
|
|
|
. Условие,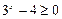 
выполнено.
№ 4.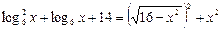 
На области допустимых значений [-4;4] исходное уравнение равносильно уравнению
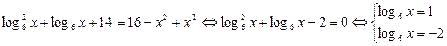. Откуда получаем 
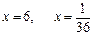. Так как 6 не принадлежит ОДЗ, то решением уравнения является 
.
Применение свойств функций. Использование ограниченности функций.
Если при решении уравнения f ( x )= g ( x ) удастся показать, что для всех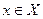 
справедливы
Неравенства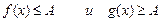 
, то на множестве Х уравнение f ( x )= g ( x ) равно-
сильно системе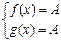 
№1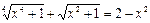 
.
Заметим, что 
Аналогично, 
.
Следовательно, левая часть уравнения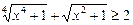 
.
Рассмотрим правую часть уравнения: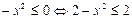 
.
Таким образом, равенство двух частей возможно тогда и только тогда, когда они
одновременно равны 2, т.е.
.
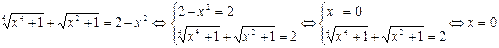Ответ: 0
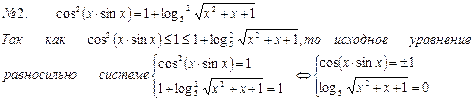
Решения второго уравнения системы х = -1 и х = 0. Первому уравнению системы
удовлетворяет только х = 0. Ответ: 0
№3. 
Левая часть уравнения представляет собой сумму двух неотрицательных функций. Равенство возможно только в том случае, когда каждое из слагаемых равно нулю.
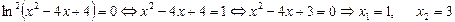
. Ответ: 3
Использование монотонности.
Утверждение 1. Если функция f возрастает (убывает) на множестве Х, то уравнение
f(x) = A на множестве Х имеет не более одного корня.
Утверждение 2. Если функция f возрастает (убывает) на множестве Х, а функция g убывает (возрастает) на множестве Х, то уравнение f ( x )= g ( x ) на множестве Х имеет не более одного корня.
|
|
|
№1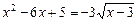 
На ОДЗ уравнения (х ≥3) функция 
возрастает, а функция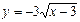 
Убывает. Уравнение может иметь не более одного корня. Подбором находим х = 4.
№2. 
Так как 0 < 1/3 < 1, то функция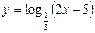 
убывает на (2,5; +∞), а функция 
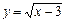возрастает. Уравнение может иметь не более одного корня
Ответ: 3
№ 2.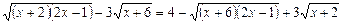 
Область допустимых значений уравнения состоит из всех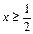 
. При таких х имеют место равенства 
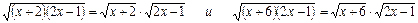. Это позволяет после очевидных преобразований переписать исходное уравнение в виде 
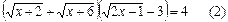. Левая часть уравнения (2) есть возрастающая функция от х, будучи произведением возрастающих функций. Значит, она может принимать значение 4 не более чем в одной точке. Несложным подбором можно убедиться, что годится х = 7.
№3.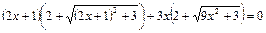 
Рассмотрим функцию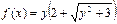 
. Ввиду того, что 
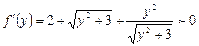, она возрастает на всей прямой. Исходное уравнение легко переписать в виде 
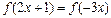, что вследствие монотонности f эквивалентно уравнение 
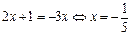. Ответ: 
.
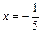Метод решения уравнений путем нахождения и исследования ОДЗ.
Если уравнение кажется на первый взгляд достаточно сложным, то следует начать его решения с нахождения ОДЗ.
|
|
|
Решить уравнение: 
.
ОДЗ: 
Область допустимых значений состоит из единственного значения. Проверим, является
ли это значение корнем уравнения.
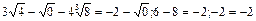. Следовательно, x =1 корень нашего
уравнения. Ответ: 1
Дата добавления: 2020-04-08; просмотров: 101; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!