Примеры заданий ЕГЭ с пирамидой
Пример 1. Отрезок Р N , равный 8, — диаметр сферы. Точки М, L лежат на сфере так, что объем пирамиды Р N М L наибольший (рис. 22). Найдите площадь треугольника К L Т, где К и Т — середины ребер РМ и N М соответственно.
Решение. Пусть О — центр сферы, а R — ее радиус. Поскольку Р N = 2R = 8 и точки М и L лежат на сфере, то ОР = О L = О N = ОМ = R = 4. Сечения сферы плоскостями Р LN и РМ N — окружности радиуса R = 4,описанные около треугольников Р LN и РМ N , причем 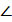 РМ N =
РМ N = 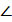 Р LN = 90°, как вписанные углы, опирающиеся на диаметр Р N .
Р LN = 90°, как вписанные углы, опирающиеся на диаметр Р N .
Пусть Н — высота пирамиды, опущенная из вершины М, а h — высота треугольника Р LN , проведенная к стороне Р N . Поскольку точка М лежит на сфере, а плоскость Р LN содержит центр сферы, то Н 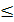 R , причем Н = R , если МО
R , причем Н = R , если МО 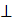 Р NL . Аналогично, так как точка L лежит на сфере, то h
Р NL . Аналогично, так как точка L лежит на сфере, то h 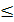 R , причем h= R , если L О
R , причем h= R , если L О  Р N .
Р N .
Отсюда для объема пирамиды Р N М L имеем
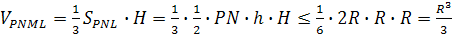
При этом
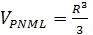 ,
,
если 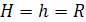 .
.
Таким образом, пирамида Р N М L имеет наибольший объем, если треугольники Р LN и РМ N прямоугольные, равнобедренные с общей гипотенузой Р N, лежащие во взаимно перпендикулярных плоскостях. Так как треугольники L О N , L ОР, L ОМ, РОМ, N ОМ равны по двум катетам, то треугольники L М N и L МР правильные со стороной
NL =Р L = ON 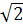 =4
=4 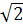
Отсюда следует, что медианы L К и L Т этих треугольников равны, причем
L К =  = 2
= 2 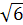 .
.
Треугольник К L Т равнобедренный, и его высота LD является медианой прямоугольного равнобедренного треугольника L ОМ. Отсюда
|
|
|
LD = 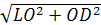 =
= 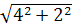 2
2 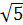 .
.
КТ — средняя линия треугольника РМ N и поэтому КТ = 0,5Р N =R . Следовательно, площадь S К L Т =  КТ
КТ  LD = 4
LD = 4 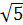 .
.
Ответ: 4  .
.

Рис.23
Пример 2. В правильной треугольной пирамиде сторона основания равна 5, а боковые рёбра наклонены к основанию под углом 60о. Найдите радиус, описанной вокруг пирамиды сферы.
Решение. Пусть АВСМ указанная пирамида (см. рис. 23) Центр описанной сферы лежит на высоте пирамиды, т. к. пирамида правильная.
Основание высоты пирамиды – центр треугольника АВС, т. е. точка пересечения медиан. Тогда:
СН=  СТ =
СТ = 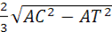 СН=
СН=  =
= 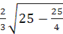 =
= 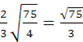 .
.
Теперь рассмотрим треугольник МНС. Здесь угол МСН равен 60о, как угол между боковым ребром МС и основанием АВС. Угол НМС равен30  . МО=ОС как радиусы. Значит, треугольник МОСравнобедренный. Как известно, в равнобедренном треугольнике углы при основании равны. Следовательно,
. МО=ОС как радиусы. Значит, треугольник МОСравнобедренный. Как известно, в равнобедренном треугольнике углы при основании равны. Следовательно,
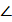 ОСМ =
ОСМ = 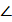 ОМС = 30
ОМС = 30 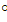 ,
, 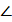 ОСН =
ОСН = 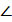 МСН -
МСН - 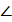 МСО = 60
МСО = 60  - 30
- 30 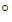 = 30
= 30  .
.
Из прямоугольного треугольника ОСН определим гипотенузу ОС, используя связь тригонометрических функций в прямоугольном треугольнике:
ОС = 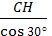 =
= 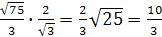 .
.
Ответ: OC =  .
.
Примеры заданий ЕГЭ с призмой

Рис.25
Пример 1. Основанием призмы служит треугольник со сторонами a , b , c . Высота призмы h (рис 25). Найти радиус описанной сферы.
|
|
|
Решение. Поскольку около призмы описана сфера, то призма прямая и её боковое ребро равно высоте. Радиус окружности, описанной около основания призмы, вычисляется по формуле
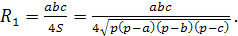
Тогда 
Ответ: 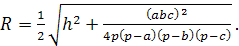
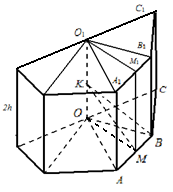
Рис.26
Пример 2. Радиус шара R . В шар вписана правильная п-угольная призма, высота которой 2 h (рис 26). Найти сторону основания призмы.
Решение. Пусть К – центр описанного шара. Имеем: KB = R, OK = h. Пусть ОМ  АВ, тогда
АВ, тогда
OB = 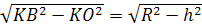
(из треугольника OKB).
Из треугольника OMB находим
a =2MB =2OB 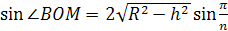 .
.
Итак, a = 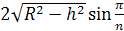 .
.
Ответ: a = 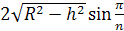 .
.
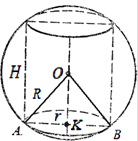
Рис.27
Дата добавления: 2020-01-07; просмотров: 96; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
