Примеры олимпиадных заданий с пирамидой
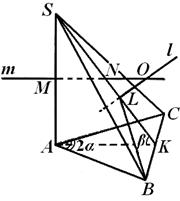
Рис.6
Пример 1. В треугольной пирамиде S АВС ребро ВС равно а, АВ=АС, ребро S А перпендикулярно к основанию АВС пирамиды, двугранный угол при ребре S А равен 2α, а при ребре ВС равен β (рис. 6). Найти радиус описанного шара.
Решение. Рассмотрим пирамиду S АВС, о которой идет речь в условии задачи. Поскольку ребро SA перпендикулярно к плоскости основания, то 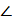 ВА S =
ВА S = 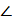 CAS = 90°, а потому угол ВАС какраз и является линейным углом двугранного угла при ребре SA. Таким образом, в основании пирамиды лежит равнобедренный треугольник с углом 2α при вершине, а высота пирамиды совпадает с ребром S А.
CAS = 90°, а потому угол ВАС какраз и является линейным углом двугранного угла при ребре SA. Таким образом, в основании пирамиды лежит равнобедренный треугольник с углом 2α при вершине, а высота пирамиды совпадает с ребром S А.
Так как проекции боковых ребер SB и S С на плоскость основания равны, то и сами эти ребра равны. Поэтому грань В S С — равнобедренный треугольник, и его высота, опущенная из вершины S, попадает в середину К ребра ВС. По теореме о трех перпендикулярах АК — высота треугольника ВАС. Отсюда ясно, что угол S КА — линейный угол двугранного угла при ребре ВС, т. е. 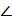 S КА = β.
S КА = β.
Центр описанного шара лежит на пересечении прямой l, перпендикулярной к плоскости В S С и проходящей через центр окружности, описанной около треугольника В S С, с плоскостью, проходящей через середину ребра А S перпендикулярно к нему. Прямая l лежит в плоскости А S К: в самом деле, плоскость В S С проходит через прямую ВС, перпендикулярную к плоскости А S К, т. е. плоскости В S С и А S К перпендикулярны; в то же время прямая l перпендикулярна к плоскости В S С и проходит через линию пересечения этих плоскостей, так что она лежит в плоскости А S К.
|
|
|
Итак, центр шара лежит в плоскости А S К. Вынесем эту плоскость на специальный чертеж. Центр шара О будет тогда лежать на пересечении прямой l и прямой m, перпендикулярной к А S и проходящей через его середину. Но, вообще говоря, могут представиться три возможности: прямые l и т пересекаются внутри, или вне треугольника А S К или на его стороне, и нам придется рассмотреть все эти возможности (см. рис. 7, 8, 9). Ниже, в ходе выкладок, мы покажем, что две из них на самом деле не осуществляются. Нас интересует радиус R описанного шара, т.е. расстояние от точки О — точки пересечения перпендикуляров т и l ксторонам угла К S А — до точки S, вершины этого угла. Прежде всего отыщем SL — проекцию искомого расстояния на сторону SK треугольника KAS. Так как в треугольнике АК B (рис. 6) нам известен катет ВК=  а и угол КАВ = α, то АК=
а и угол КАВ = α, то АК=  а ctg α.
а ctg α.
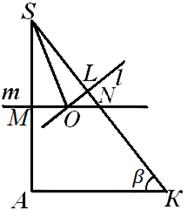
Рис. 7
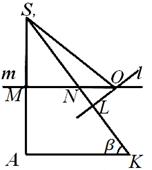
Рис.8
Далее, из треугольника КА S имеем
SK = 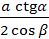 .
.
Так как L — центр описанной около треугольника В S С окружности, то LS = L В, aпотому из треугольника ВК L находим, что ( S К- SL )2+КВ2=В L2, т. е.
SL= 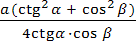 .
.
Отметив, что проведенные вычисления отрезка SL никак не зависели от местоположения центра О описанного шара, вернемся к рис. 7, 8, 9. Обозначим через N точку пересечения прямой m со стороной S К. Ясно, что прямые l и т пересекаются вне треугольника КА S , если SN<SL (рис. 8); если же S N > SL , то точка О лежит внутри этого треугольника (рис. 7); наконец, если SN = SL , то точка О лежит на стороне S К этого треугольника (рис. 9). Выясним, какое из этих положений имеет место на самом деле.
|
|
|

Рис.9
Так как МN — средняя линия треугольника КА S , то SN =  S К. Сравнивая длины отрезков SN и SL, без труда докажем, что при любых а, α и
S К. Сравнивая длины отрезков SN и SL, без труда докажем, что при любых а, α и
β 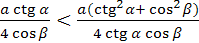
(из геометрических соображений следует, что а > 0, 0° < 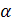 < 90° и 0° < β < 90°). Следовательно, каковы бы ни были размеры а, α и β пирамиды S АВС, центр О описанного шара всегда лежит вне пирамиды. Это в свою очередь означает, что вынесенная нами плоская конфигурация в плоскости КА S может иметь лишь вид, указанный на рис 8; расположения, изображенные на рис. 7 и 9, в действительности иметь места не могут. Рассматривая рис. 8, легко покажем, что
< 90° и 0° < β < 90°). Следовательно, каковы бы ни были размеры а, α и β пирамиды S АВС, центр О описанного шара всегда лежит вне пирамиды. Это в свою очередь означает, что вынесенная нами плоская конфигурация в плоскости КА S может иметь лишь вид, указанный на рис 8; расположения, изображенные на рис. 7 и 9, в действительности иметь места не могут. Рассматривая рис. 8, легко покажем, что 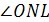 = β, а потому LO = NL tgβ = (SL—S N)tgβ. Подставляя сюда полученные выше выражения для SL и S N, получаем после очевидных вычислений:
= β, а потому LO = NL tgβ = (SL—S N)tgβ. Подставляя сюда полученные выше выражения для SL и S N, получаем после очевидных вычислений:
L О =  а tgα
а tgα  sinβ.
sinβ.
Наконец, из прямоугольного треугольника О LS находим
|
|
|
R = 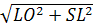 =
=  .
.
Как видим, выкладки в задаче оказались простыми — главная трудность решения лежит в рассуждениях, устанавливающих положение центра описанного шара.
Ответ: R = 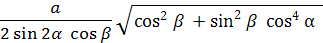 .
.
Пример 2. В шар радиуса R вписана правильная треугольная пирамида с плоским углом при вершине. Найти объем пирамиды, а также боковую поверхность конуса, описанного около указанной пирамиды.
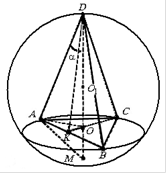
Рис.10
Решение. Пусть сторона основания пирамиды равна a, радиус основания конуса, описанного около этой пирамиды равен r, тогда  (рис. 10). Грани пирамиды – равнобедренные треугольники. Тогда DK – высота, медиана и биссектриса ABD. Из прямоугольного треугольника ADK имеем
(рис. 10). Грани пирамиды – равнобедренные треугольники. Тогда DK – высота, медиана и биссектриса ABD. Из прямоугольного треугольника ADK имеем 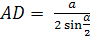 . Высоту пирамиды найдем из прямоугольного треугольника AOD:
. Высоту пирамиды найдем из прямоугольного треугольника AOD:
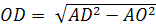 ,
, 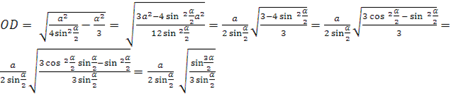 .
.
DM – диаметр шара. Тогда в сечении шара, проходящем через диаметр DM и точку А, получим прямоугольный треугольник AMD. Из метрических соотношений в прямоугольном треугольнике имеем 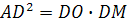 ,
,
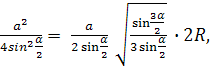 откуда
откуда 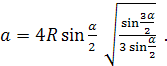
Тогда площадь основания найдем по формуле:
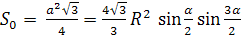 .
.
И из формулы 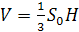 находим объем пирамиды:
находим объем пирамиды:
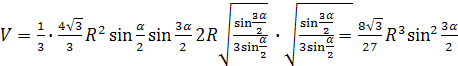 .
.
Ребро AD по определению описанного конуса является его образующей. Тогда найдем боковую поверхность описанного конуса по формуле Sбок = r l:
|
|
|
 .
.
Ответ: 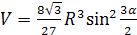 ;
; 
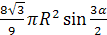 .
.
Пример 3. В основании пирамиды лежит квадрат со стороной а. Высота пирамиды проходит через середину одного из ребер основания и равна 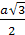 . Найти радиус сферы, описанной около пирамиды.
. Найти радиус сферы, описанной около пирамиды.
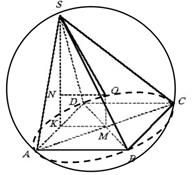
Рис.11
Решение. Типичной ошибкой при решении этой задачи является утверждение о том, что центр описанной сферы находится на грани SBC (рис. 11). В действительности положение точки О не связано с гранью SBC.
В силу равноудаленности точки О от вершин S, A, B, C, D следует, что OABCD – правильная четырехугольная пирамида. Следовательно, на грань ABCD точка О проектируется в точку М – точку пересечения диагоналей. Треугольник ASD равнобедренный, тогда высота пирамиды SK является медианой треугольника ASD, 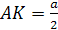 . Из прямоугольного треугольника SAK найдем SA:
. Из прямоугольного треугольника SAK найдем SA:
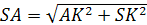 ,
, 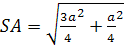
Следовательно, треугольник SAD – равносторонний и OASD – правильная треугольная пирамида. Тогда точка О проектируется на грань SAD в центр треугольника SAD . Отсюда
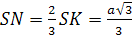 ,
, 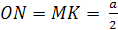 .
.
Из треугольника SON находим искомый радиус SO,
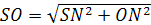 ,
, 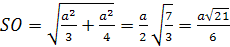 .
.
Ответ: 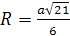 .
.
Пример 4. В шар радиуса R вписана правильная шестиугольная усечённая пирамида, у которой плоскость нижнего основания проходит через центр шара, а боковое ребро составляет с плоскостью основания угол 60  . Определить объём пирамиды.
. Определить объём пирамиды.
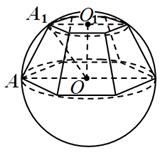
Рис.12
Решение. По условию, 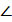 OAA1 = 60
OAA1 = 60  (рис. 12); значит,
(рис. 12); значит,
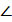 О1ОА1=30
О1ОА1=30  и А1О1 =
и А1О1 =  А1О =
А1О =  ,OO1 =
,OO1 = 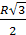 .
.
Находим
Sнижн.осн.= 6 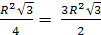 , Sверхн. осн.=
, Sверхн. осн.= 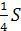 нижн. осн.
нижн. осн. 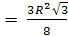 .
.
Окончательно получим
 .
.
Ответ: 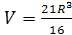
Дата добавления: 2020-01-07; просмотров: 233; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
